1 梯度具体是怎么下降的?

∂ J ( θ ) ∂ θ \frac{\partial J (\theta )}{\partial \theta} ∂θ∂J(θ)(损失函数:用来衡量模型预测值与真实值之间差异的函数)
对损失函数求导,与学习率相乘,按梯度反方向与 θ n \theta^n θn相减,使 θ n \theta^n θn的值与 y y y目标值的越来越接近,从而得到最优解。最小化损失函数
以下是一些常见的损失函数:
-
均方误差(Mean Squared Error,MSE):MSE 是回归问题中常用的损失函数,计算预测值与真实值之间差的平方的均值。
MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 MSE=n1∑i=1n(yi−y^i)2
-
交叉熵损失函数(Cross-Entropy Loss):交叉熵通常用于分类问题中,特别是多分类问题。对于二分类问题,交叉熵损失函数可以写为:
Cross-Entropy Loss = − 1 n ∑ i = 1 n ( y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ) \text{Cross-Entropy Loss} = - \frac{1}{n} \sum_{i=1}^{n} \left( y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right) Cross-Entropy Loss=−n1∑i=1n(yilog(y^i)+(1−yi)log(1−y^i))
其中 ( y i ) ( y_i ) (yi)是真实类别(0 或 1), ( y ^ i ) ( \hat{y}_i) (y^i) 是模型对样本属于正类的预测概率。
-
对数损失函数(Log Loss):对数损失函数也用于二分类问题中,它与交叉熵损失函数类似。
Log Loss = − 1 n ∑ i = 1 n ( y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ) \text{Log Loss} = - \frac{1}{n} \sum_{i=1}^{n} \left( y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right) Log Loss=−n1∑i=1n(yilog(y^i)+(1−yi)log(1−y^i))
-
Hinge Loss:Hinge Loss 通常用于支持向量机(SVM)中,适用于二分类问题。
Hinge Loss = 1 n ∑ i = 1 n max ( 0 , 1 − y i ⋅ y ^ i ) \text{Hinge Loss} = \frac{1}{n} \sum_{i=1}^{n} \max(0, 1 - y_i \cdot \hat{y}_i) Hinge Loss=n1∑i=1nmax(0,1−yi⋅y^i)
这些是常见的损失函数,但根据具体问题的特点和模型类型,也可以使用其他类型的损失函数。在梯度下降优化过程中,目标是最小化损失函数,通过调整模型参数使得损失函数的值最小化,从而得到最优的模型参数。
2 常用梯度下降法优缺点
2.1 优缺点
| 梯度下降 | 优点 | 缺点 |
|---|---|---|
| 批量梯度下降BGD | 能够全局性地更新模型参数,收敛稳定 | 计算成本高,特别是在大数据集上; 每次迭代都要遍历整个数据集,更新速度较慢 |
| 随机梯度下降SGD | 更新速度快,对大规模数据集具有较好的适应性; 可以跳出局部最优解 | 更新方向不稳定,存在随机性; 可能会产生较大的参数更新波动 |
| 小批量梯度下降MBGD | 综合了 BGD 和 SGD 的优点,既能够全局性地更新模型参数,又能够降低计算成本,提高更新速度 | 需要选择合适的小批量大小,不同的大小可能会影响算法的性能;需要调整学习率等超参数。 |
2.2 代码实现
批量梯度下降
import numpy as np# 1、初始化x y
# 100 行 二维 1 个数
X = np.random.randn(100, 1)
# 0-10 1维2个数
w, b = np.random.randint(0, 10, size=2)
print(w, b)
# 构建截距
y = X.dot(w) + b + np.random.rand(100, 1)
print(X.shape, y.shape)# 2、使用偏置项x_0 = 1,更新X
X = np.concatenate([X, np.full(shape=(100, 1), fill_value=1)], axis=1)
print(X.shape, y.shape)# 3、创建超参数轮次
epochs = 10000# 4、初始化 W0...Wn,标准正太分布创建 W
# 矩阵运算:2列2行 m*n*n*k = m*k X追加了偏置项
theta = np.random.randn(2, 1)# 5、设置学习率
t0, t1 = 5, 1000def learn_rate(t):return t0 / (t + t1)# 6、梯度下降
for i in range(epochs):g = X.T.dot((X.dot(theta) - y))theta = theta - learn_rate(i) * gprint('真实斜率和截距是:', w, b)
print('梯度下降计算斜率和截距是:', theta)
小批量梯度下降
import numpy as np# 1、创建数据集X,y
X = np.random.rand(100, 3)
w = np.random.randint(1, 10, size=(3, 1))
b = np.random.randint(1, 10, size=1)
y = X.dot(w) + b + np.random.randn(100, 1)# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]# 3、创建超参数轮次、样本数量
epochs = 10000
n = 100# 4、定义一个函数来调整学习率
t0, t1 = 5, 500def learning_rate_schedule(t):return t0 / (t + t1)# 5、初始化 W0...Wn,标准正太分布创建W
theta = np.random.randn(4, 1)# 6、多次for循环实现梯度下降,最终结果收敛
def take_data():index = np.arange(100)# 重新洗牌np.random.shuffle(index)X_ = X[index]y_ = y[index]# 一次取一批数据10个样本X_batch = X_[0: 10]y_batch = y_[0: 10]return X_batch, y_batchfor epoch in range(epochs):X_i, y_i = take_data()theta = theta - learning_rate_schedule(epoch) * (X_i.T.dot(X_i.dot(theta) - y_i))print('真实斜率和截距是:', w, b)
print('梯度下降计算斜率和截距是:', theta)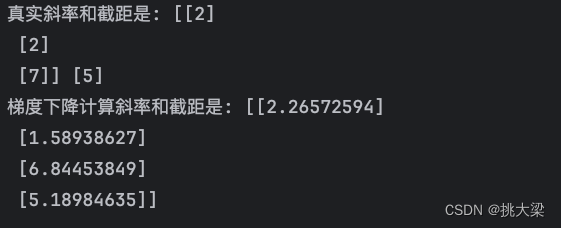
随机梯度下降
import numpy as np# 1、创建数据集X,y
X = 2 * np.random.rand(100, 1)
w, b = np.random.randint(1, 10, size=2)
y = X.dot(w) + b + np.random.randn(100, 1)# 2、使用偏置项x_0 = 1,更新X
X = np.c_[X, np.ones((100, 1))]# 3、创建超参数轮次、样本数量
epochs = 100# 4、定义一个函数来调整学习率
t0, t1 = 5, 500def learning_rate_schedule(t):return t0 / (t + t1)# 5、初始化 W0...Wn,标准正太分布创建W
theta = np.random.randn(2, 1)
# 6、多次for循环实现梯度下降,最终结果收敛
for epoch in range(epochs):X_i = X[np.random.randint(0, 100, size=1)]y_i = y[np.random.randint(0, 100, size=1)]theta = theta - learning_rate_schedule(epoch) * (X_i.T.dot(X_i.dot(theta) - y_i))print('真实斜率和截距是:', w, b)
print('梯度下降计算斜率和截距是:', theta)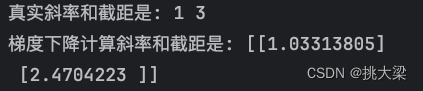
3 梯度下降存在的一些问题
虽然梯度下降是一种常用且有效的优化算法,但在实际应用中也存在一些问题和挑战。以下是机器学习中梯度下降存在的一些常见问题:
-
局部最优解: 梯度下降可能会陷入局部最优解中而无法找到全局最优解。特别是在非凸优化问题中,存在多个局部最优解,而梯度下降算法容易受初始参数值的影响而收敛到局部最优解。
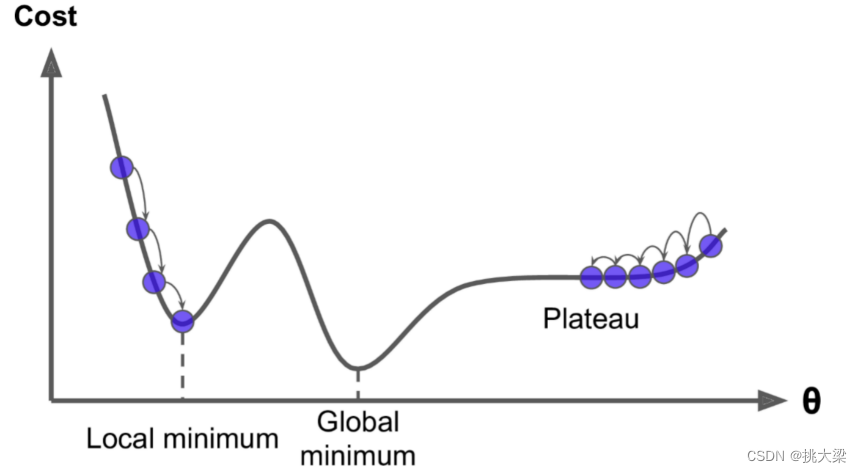
-
学习率选择: 学习率是梯度下降中的关键超参数,选择不当可能导致算法无法收敛或收敛速度过慢。学习率过大会导致震荡或发散,学习率过小会导致收敛速度缓慢。

-
鞍点问题: 在高维空间中,梯度下降可能会受到鞍点的影响而陷入停滞状态。鞍点是目标函数在某些方向上是局部最小值,而在其他方向上是局部最大值的点,梯度为零,使得梯度下降无法继续进行。
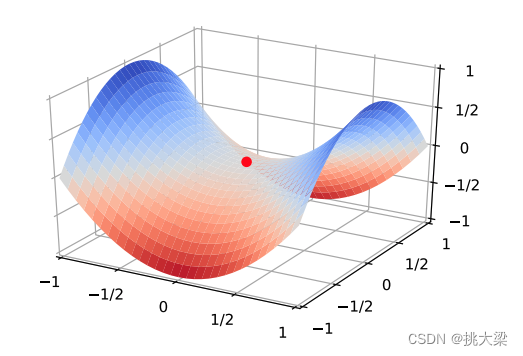
-
过拟合: 当模型复杂度过高或训练数据过少时,梯度下降可能会导致模型过拟合,即在训练集上表现良好,但在测试集上表现较差。
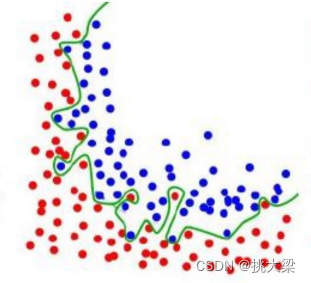
-
欠拟合:模型在训练数据上无法捕捉到数据的真实规律,表现为模型过于简单,无法很好地拟合数据的特征和复杂性。
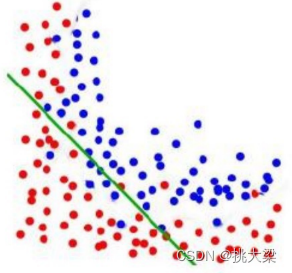
泛化能力强的:
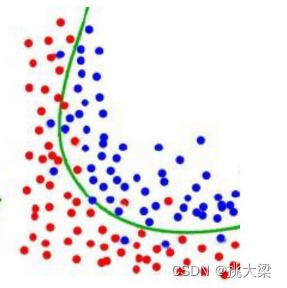
-
高维问题: 在高维空间中,梯度下降算法可能面临维度灾难(curse of dimensionality)的挑战,即随着特征空间维度的增加,优化问题变得更加复杂,梯度下降算法的效率会大大降低。

4 梯度下降常用优化
要提高机器学习中梯度下降算法的性能和效率,可以采取以下几种方法:
-
随机梯度下降(SGD)的变体: 随机梯度下降算法的变体,如Mini-batch SGD、Momentum SGD、Adaptive Moment Estimation (Adam)等,可以结合随机性和自适应性,提高算法的效率和性能。
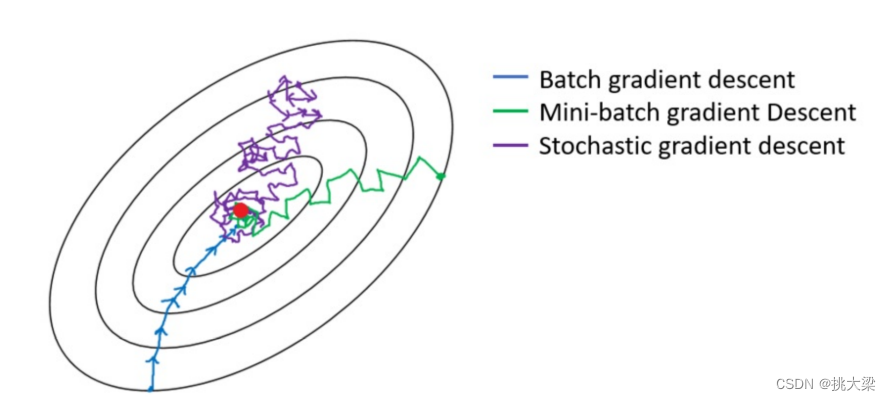
-
参数初始化策略: 使用合适的参数初始化策略,如Xavier初始化、He初始化等,可以加速模型的收敛速度,减少训练时间。
-
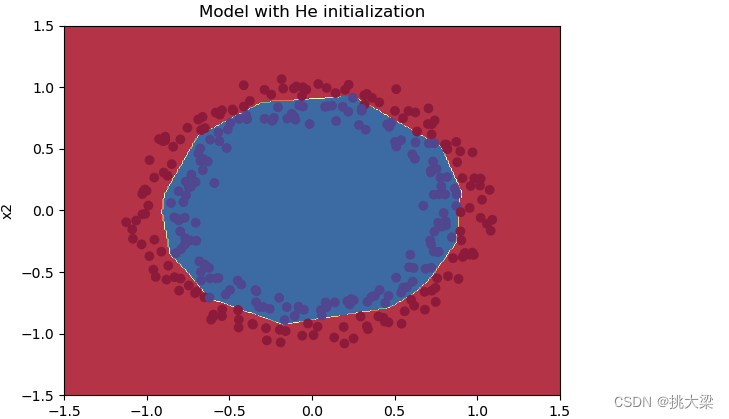
-
正则化技术: 使用正则化技术,如L1正则化、L2正则化等,可以防止过拟合,提高模型的泛化能力,进而提高算法的性能。
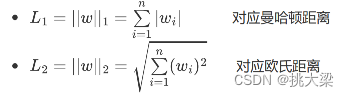
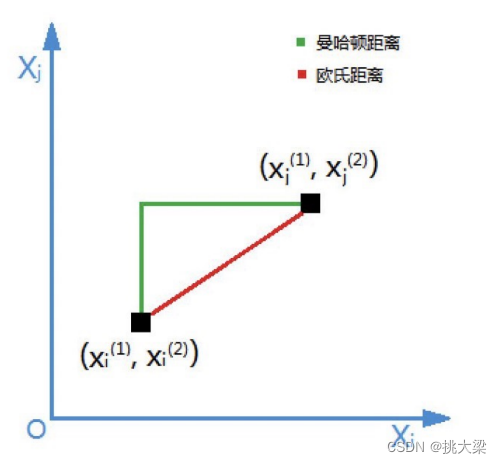
-
批归一化: 在深度神经网络中使用批归一化技术,可以加速收敛速度,提高模型的稳定性和泛化能力,进而提高算法的性能。
 6. 学习率衰减: 在训练过程中逐渐减小学习率,可以帮助模型更好地收敛到最优解,防止学习率过大导致的参数更新波动或震荡现象。
6. 学习率衰减: 在训练过程中逐渐减小学习率,可以帮助模型更好地收敛到最优解,防止学习率过大导致的参数更新波动或震荡现象。
t0, t1 = 5, 1000def learn_rate(t):return t0 / (t + t1)
- 集成学习方法: 使用集成学习方法,如Bagging、Boosting等,可以结合多个模型的预测结果,降低模型的方差,提高模型的性能和鲁棒性。
# 导入必要的库
from sklearn.ensemble import BaggingClassifier, GradientBoostingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 生成样本数据
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)# 将数据分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# Bagging集成学习
bagging_clf = BaggingClassifier(base_estimator=DecisionTreeClassifier(), n_estimators=10, random_state=42)
bagging_clf.fit(X_train, y_train)
bagging_pred = bagging_clf.predict(X_test)
bagging_accuracy = accuracy_score(y_test, bagging_pred)
print("Bagging集成学习准确率:", bagging_accuracy)# Boosting集成学习
boosting_clf = GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, random_state=42)
boosting_clf.fit(X_train, y_train)
boosting_pred = boosting_clf.predict(X_test)
boosting_accuracy = accuracy_score(y_test, boosting_pred)
print("Boosting集成学习准确率:", boosting_accuracy)