联合体类型的声明

联合体（Union）是一种特殊的数据类型，它允许在同一内存位置存储不同类型的数据。与结构体不同的是，联合体的所有成员共享同一块内存空间，因此联合体的大小取决于它最大的成员的大小。

union MyUnion {int intValue;float floatValue;
};

#include <stdio.h>
//联合类型的声明
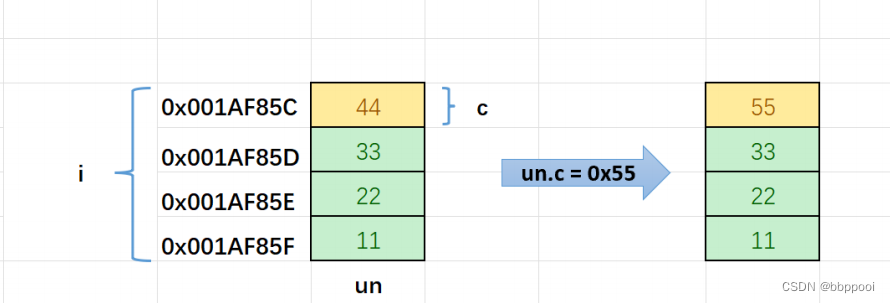
union Un
{char c;int i;
};
int main()
{//联合变量的定义union Un un = {0};//计算连个变量的⼤⼩printf("%d\n", sizeof(un));
return 0；
}

struct S
{char c;int i;
};
struct S s = {0}

union Un
{char c;int i;
};
union Un un = {0};

联合体大小的计算

联合体的大小取决于它最大的成员的大小，因为所有成员共享同一块内存空间。具体计算方式如下：

1. 找出联合体中所有成员中的最大成员的大小。
2. 联合体的大小即为最大成员的大小。

struct gift_list
{int stock_number;//库存量double price; //定价int item_type;//商品类型union{struct{char title[20];//书名char author[20];//作者int num_pages;//⻚数}book;struct{char design[30];//设计}mug;struct{char design[30];//设计int colors;//颜⾊int sizes;//尺⼨}shirt;}item;
};

枚举类型的声明

枚举（Enum）类型用于定义一组命名的整数常量。在C语言中，可以使用 enum 关键字来声明枚举类型。

一般的声明语法如下：

enum EnumName {EnumConstant1,EnumConstant2,// ...
};

 其中，EnumName 是枚举类型的名称，EnumConstant1、EnumConstant2 等是枚举常量，它们是整数值，按照默认规则从0开始递增。

enum Day//星期
{Mon,Tues,Wed,Thur,Fri,Sat,Sun
};
enum Sex//性别
{MALE,
FEMALE,SECRET
}；
enum Color//颜⾊
{RED,GREEN,BLUE
};

enum Color//颜⾊
{RED=2,GREEN=4,BLUE=8
};

枚举类型的优点

1. 可读性强： 枚举类型使得代码更具可读性。通过为一组相关的常量定义一个枚举类型，可以使代码更加清晰和易于理解。使用有意义的标识符来表示枚举常量，可以让代码的含义更加明确。

2. 类型安全性： 枚举类型提供了一种类型安全的方式来表示一组相关的常量。在编译时，编译器会检查枚举类型中的值是否属于枚举中定义的范围，从而帮助避免因类型错误引起的潜在问题。

3. 可扩展性： 枚举类型提供了一种灵活的方式来表示一组可能会随着时间变化而增加的常量。通过添加新的枚举常量，可以轻松地扩展现有的枚举类型，而不会对现有代码产生太大的影响。

4. 编译器优化： 一些编译器可以对枚举类型进行优化，将其转换为更高效的表示方式，从而提高代码的执行效率。例如，编译器可以将枚举常量转换为整数或其他底层类型，以减少内存占用和运行时开销。

5. 可移植性： 枚举类型的语法在大多数编程语言中都是通用的，因此代码具有良好的可移植性。无论在哪种编程环境中，枚举类型都可以被广泛地支持和使用。

枚举类型的使用

enum Color//颜⾊
{RED=1,GREEN=2,BLUE=4
};
enum Color clr = GREEN;//使⽤枚举常量给枚举变量赋值