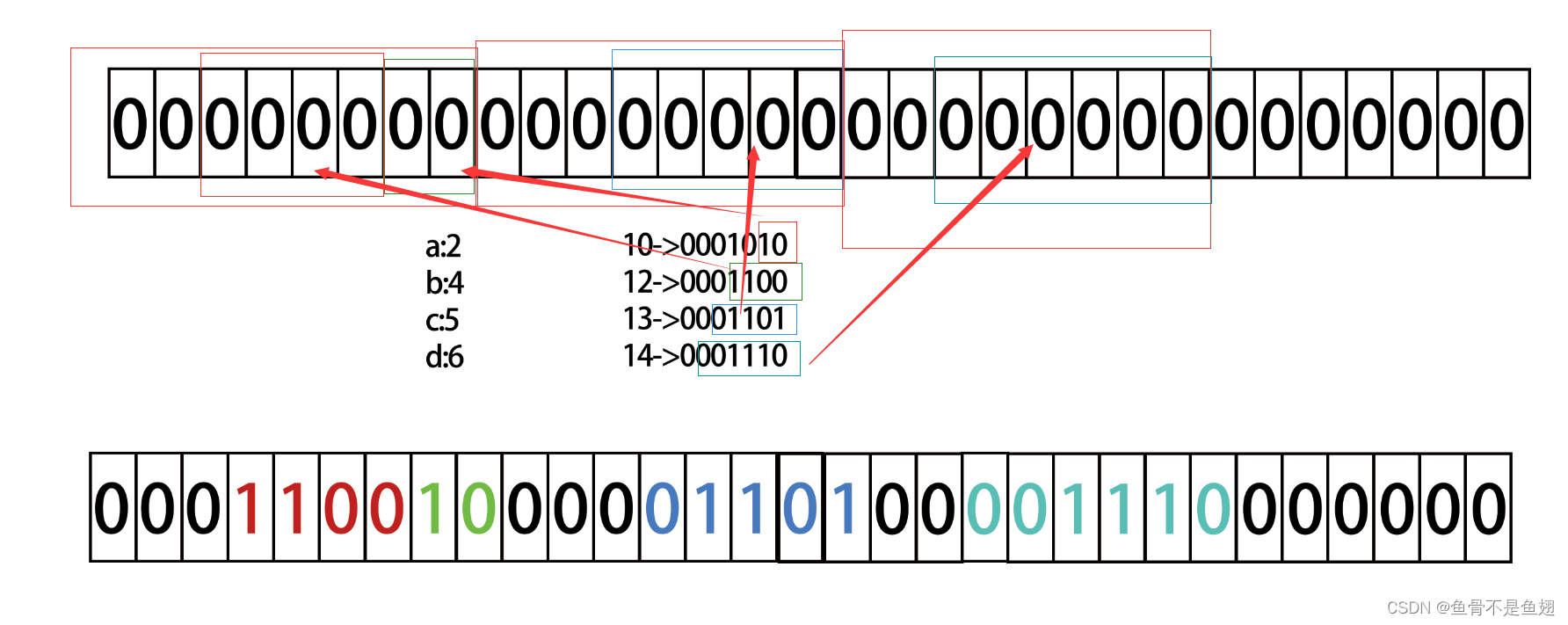
在温故数据合并的时候突然想起数电的 卡诺图.
根据合并一位不同的原则, 使用 python 做了一个实现, 感觉和QM算法不太一样:
# 判断两个数是否只有一个二进制不一样
def nor(x1, x2):return x1^x2# 判断两个集合是否相邻, 只有一位不同
def is_track(x1, x2):ts = [nor(x1[i],x2[i]) for i in range(len(x1))]k = 0 for t in ts: k |= t if k == 0: return Falsek = math.log2(k) return k == int(k) # # 将所有数据进行分组和比对
def sfun(xs, ts):xs_t = []if len(xs) == 0: return xs_i = [] # 记录已经添加过的结构for i in range(len(xs)-1):etr = Falsefor j in range(i+1, len(xs)):if is_track(xs[i],xs[j]):xs_t.append(xs[i]+xs[j])xs_i += [i, j]etr = True# 将不能合并的数据丢在完成缓冲区xs_it = set(xs_i)if not etr and i not in xs_it: ts.append(xs[i])sfun(xs_t, ts)# 输入数据
t = [0,1,2,3,4]
# 数据处理一下
t.sort() # 做一个排序
xs = [[x] for x in t] # 将元素变成列表供下面sfun递归参数统一
ts = [] # 保存分组好的数据
sfun(xs, ts)
# 由于合并的过程没管理好,导致有多个重复的结果,做个去重
ts_ = []
for t in ts:t.sort()t =set(t)if t not in ts_:ts_.append(t)# 输出分组
print(ts_)
还是有些问题,
输入: [2,3,7,9,10,11,12,13,18,19,22,23,26,27,30,31]
程序输出: [{9, 11}, {9, 13}, {12, 13}, {19, 3, 23, 7}, {2, 3, 10, 11, 18, 19, 26, 27}, {18, 19, 22, 23, 26, 27, 30, 31}]
正确输出应该是:
[{9, 11}, {12, 13}, {19, 3, 23, 7}, {2, 3, 10, 11, 18, 19, 26, 27}, {18, 19, 22, 23, 26, 27, 30, 31}]
[{9, 13}, {12, 13}, {19, 3, 23, 7}, {2, 3, 10, 11, 18, 19, 26, 27}, {18, 19, 22, 23, 26, 27, 30, 31}]
我想到的是加个元素过滤的方法来处理, 目前还没有想到更完美的解释和解决方案, 有大大看出来的话, 欢迎评论区交流.
好吧实现没有问题,只是还有一步没有做.
其中 Q-M(Quine-McCluskey)法化简布尔表达式 博文提到:

所以QM算法里面要做个"素项表" 的过滤, 然后应该就会没问题.
参考:
- Q-M法,python自动化简逻辑表达式,卡诺图化简。
- [数电]用python实现卡诺图化简,自动化简逻辑表达式
- Q-M(Quine-McCluskey)法化简布尔表达式