目录
介绍:
模板:
例子:择偶
极小型指标转化为极大型(正向化):
中间型指标转为极大型(正向化):
区间型指标转为极大型(正向化):
标准化处理:
公式:
熵权:
公式:
完整代码:
结果:
介绍:
熵权法是一种多属性决策方法,用于确定各个属性在决策中的重要程度。该方法的核心思想是通过计算属性的熵值,来评估属性的信息量和不确定性,进而确定属性的权重。
熵是信息论中的概念,表示一个随机变量的不确定性。在决策中,一个属性的熵越大,说明该属性对决策的贡献越大,因为它包含了更多的信息。熵权法通过计算属性的熵,然后将每个属性的熵除以总的熵,得到每个属性的权重。
具体步骤如下:
- 收集决策所涉及的属性数据。
- 计算每个属性的熵值,使用熵的计算公式:熵 = -Σ(p*log2(p)),其中p表示属性的概率。
- 计算所有属性的熵之和,得到总的熵。
- 计算每个属性的权重,使用该属性的熵除以总的熵。
- 最后可以根据属性的权重,进行决策或排序。
熵权法在多属性决策中具有一定的优势,能够考虑到不同属性的权重,提高决策的准确性和可靠性。但是,在实际应用中,需要注意属性数据的准确性和合理性,以及熵的计算方法的选择等问题。
模板:
import numpy as np# 定义计算熵的函数
def entropy(data):# 计算每个属性的概率prob = np.array(data) / np.sum(data)# 计算熵entropy = -np.sum(prob * np.log2(prob))return entropy# 定义熵权法函数
def entropy_weight(data):# 计算每个属性的熵entropies = [entropy(column) for column in data.T]# 计算总的熵total_entropy = np.sum(entropies)# 计算每个属性的权重weights = [entropy / total_entropy for entropy in entropies]return weights# 示例数据
data = np.array([[10, 20, 30, 40], [40, 30, 20, 10]])# 计算权重
weights = entropy_weight(data)
print("属性权重:", weights)
例子:择偶

极小型指标转化为极大型(正向化):
# 公式:max-x if ('Negative' in name) == True:max0 = data_nor[columns_name[i + 1]].max()#取最大值data_nor[columns_name[i + 1]] = (max0 - data_nor[columns_name[i + 1]]) # 正向化# print(data_nor[columns_name[i+1]])中间型指标转为极大型(正向化):
# 中间型指标正向化 公式:M=max{|xi-best|} xi=1-|xi-best|/Mif ('Moderate' in name) == True:print("输入最佳值:")max = data_nor[columns_name[i + 1]].max()min = data_nor[columns_name[i + 1]].min()best=input()M=0for j in data_nor[columns_name[i + 1]]:if(M<abs(j-int(best))):M=(abs(j-int(best)))data_nor[columns_name[i + 1]]=1-(abs(data_nor[columns_name[i + 1]]-int(best))/M)#print(data_nor[columns_name[i + 1]])区间型指标转为极大型(正向化):
# 区间型指标正向化if('Section' in name)==True:print()print("输入区间:")a=input()b=input()a=int(a)b=int(b)max = data_nor[columns_name[i + 1]].max()min= data_nor[columns_name[i + 1]].min()if(a-min>max-b):M=a-minelse:M=max-b#print(data_nor[columns_name[i + 1]][0])cnt=0for j in data_nor[columns_name[i + 1]]:if(j<int(a)):data_nor[columns_name[i + 1]][cnt]=1-(a-j)/Melif (int(a)<= j <=int(b)):data_nor[columns_name[i + 1]][cnt]=1elif (j>b):data_nor[columns_name[i + 1]][cnt]=1-(j-b)/M#print(data_nor[columns_name[i + 1]][cnt])cnt+=1#print(data_nor[columns_name[i + 1]])'''公式:
M = max{a-min{xi},max{xi}-b} xi<a,则xi=1-(a-xi)/M; a<=xi<=b,则xi=1; xi>b,则1-(xi-b)/M
'''标准化处理:
公式:

def normalization(data_nor):data_nors = data_nor.valuesdata_nors = np.delete(data_nors, 0, axis=1)#去掉第一行squere_A = data_nors * data_nors#矩阵相乘# print(squere_A)sum_A = np.sum(squere_A, axis=0)#按列求和sum_A = sum_A.astype(float)stand_A = np.sqrt(sum_A)#平方根columns_name = data_nor.columns.valuescnt=0for i in columns_name[1:]:#print(data_nor[i])data_nor[i]=data_nor[i]/stand_A[cnt]cnt+=1#print(data_nor)return data_nor熵权:
公式:
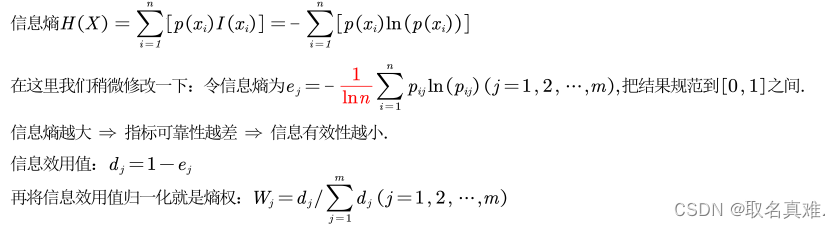
# 定义计算熵权方法
def entropy_weight(data_nor):columns_name = data_nor.columns.valuesn = data_nor.shape[0]E = []for i in columns_name[1:]:# 计算信息熵# print(i)data_nor[i] = data_nor[i] / sum(data_nor[i])data_nor[i] = data_nor[i] * np.log(data_nor[i])data_nor[i] = data_nor[i].where(data_nor[i].notnull(), 0)# print(data_nor[i])Ei = (-1) / (np.log(n)) * sum(data_nor[i])E.append(Ei)# print(E)# 计算权重W = []for i in E:wi = (1 - i) / ((len(columns_name) - 1) - sum(E))W.append(wi)# print(W)return W完整代码:
#coding=gbk
import pandas as pd
import numpy as np
import re
import warnings# 定义文件读取方法
def read_data(file):file_path = fileraw_data = pd.read_excel(file_path, header=0)# print(raw_data)return raw_data# 定义数据正向化
def data_normalization(data):data_nor = data.copy()columns_name = data_nor.columns.values#print(columns_name)for i in range((len(columns_name) - 1)):name = columns_name[i + 1]print("输入这一类数据类型(Positive、Negative、Moderate、Section:)")name=input()# 极小型指标正向化if ('Negative' in name) == True:max0 = data_nor[columns_name[i + 1]].max()#取最大值data_nor[columns_name[i + 1]] = (max0 - data_nor[columns_name[i + 1]]) # 正向化# print(data_nor[columns_name[i+1]])# 中间型指标正向化if ('Moderate' in name) == True:print("输入最佳值:")max = data_nor[columns_name[i + 1]].max()#取最大值min = data_nor[columns_name[i + 1]].min()#取最小值best=input()M=0for j in data_nor[columns_name[i + 1]]:if(M<abs(j-int(best))):M=(abs(j-int(best)))data_nor[columns_name[i + 1]]=1-(abs(data_nor[columns_name[i + 1]]-int(best))/M)#print(data_nor[columns_name[i + 1]])# 区间型指标正向化if('Section' in name)==True:print("输入区间:")a=input()b=input()a=int(a)b=int(b)max = data_nor[columns_name[i + 1]].max()min= data_nor[columns_name[i + 1]].min()if(a-min>max-b):M=a-minelse:M=max-b#print(data_nor[columns_name[i + 1]][0])cnt=0for j in data_nor[columns_name[i + 1]]:if(j<int(a)):data_nor[columns_name[i + 1]][cnt]=1-(a-j)/Melif (int(a)<= j <=int(b)):data_nor[columns_name[i + 1]][cnt]=1elif (j>b):data_nor[columns_name[i + 1]][cnt]=1-(j-b)/Mcnt+=1#print(data_nor[columns_name[i + 1]])# print(data_nor)return data_nordef normalization(data_nor):data_nors = data_nor.valuesdata_nors = np.delete(data_nors, 0, axis=1)squere_A = data_nors * data_nors#矩阵相乘# print(squere_A)sum_A = np.sum(squere_A, axis=0)#按列求和sum_A = sum_A.astype(float)stand_A = np.sqrt(sum_A)#开平方columns_name = data_nor.columns.valuescnt=0for i in columns_name[1:]:data_nor[i]=data_nor[i]/stand_A[cnt]#每个元素除以相对应的平方根cnt+=1#print(data_nor)return data_nor# 定义计算熵权方法
def entropy_weight(data_nor):columns_name = data_nor.columns.valuesn = data_nor.shape[0]E = []for i in columns_name[1:]:# 计算信息熵# print(i)data_nor[i] = data_nor[i] / sum(data_nor[i])data_nor[i] = data_nor[i] * np.log(data_nor[i])data_nor[i] = data_nor[i].where(data_nor[i].notnull(), 0)# print(data_nor[i])Ei = (-1) / (np.log(n)) * sum(data_nor[i])E.append(Ei)# print(E)# 计算权重W = []for i in E:wi = (1 - i) / ((len(columns_name) - 1) - sum(E))W.append(wi)# print(W)return W# 计算得分
def entropy_score(data, w):data_s = data.copy()columns_name = data_s.columns.valuesfor i in range((len(columns_name) - 1)):name = columns_name[i + 1]data_s[name] = data_s[name] * w[i]return data_sif __name__ == "__main__":file = 'filepath' # 声明数据文件地址data = read_data(file) # 读取数据文件data_nor = data_normalization(data) # 数据正向化,生成后的数据data_norprint("\n正向化后的数据:")print(data_nor)data_nor=normalization(data_nor)print("\n标准化后的数据:")print(data_nor)W = entropy_weight(data_nor) # 计算熵权权重data_s = entropy_score(data, W) # 计算赋权后的得分,使用原数据计算#data_nor_s = entropy_score(data_nor, W)print("\n权值:",W)print("\n赋权后的得分:")print(data_s)#print(data_nor_s)结果:

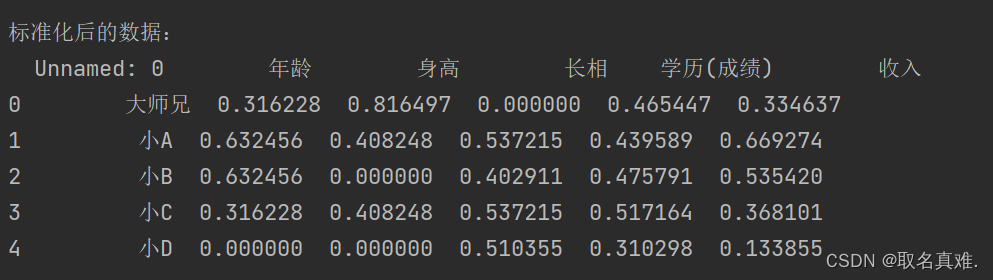
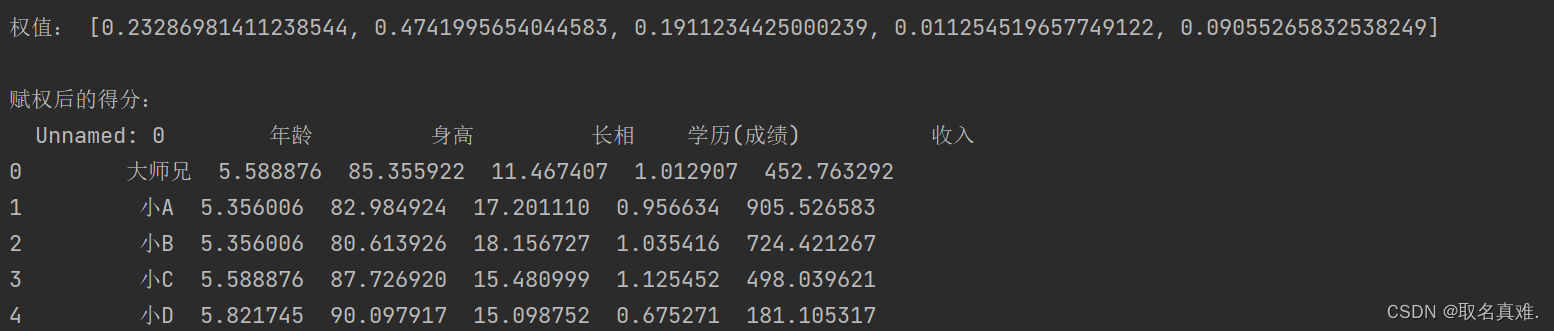


![练习 9 Web [SUCTF 2019]CheckIn (未拿到flag)](https://img-blog.csdnimg.cn/direct/ce6fbec3c49342ce90021571deaa6860.png)



![[BT]BUUCTF刷题第2天(3.20)](https://img-blog.csdnimg.cn/direct/2aa33d13ca064706876bcb2a62ed542e.png)