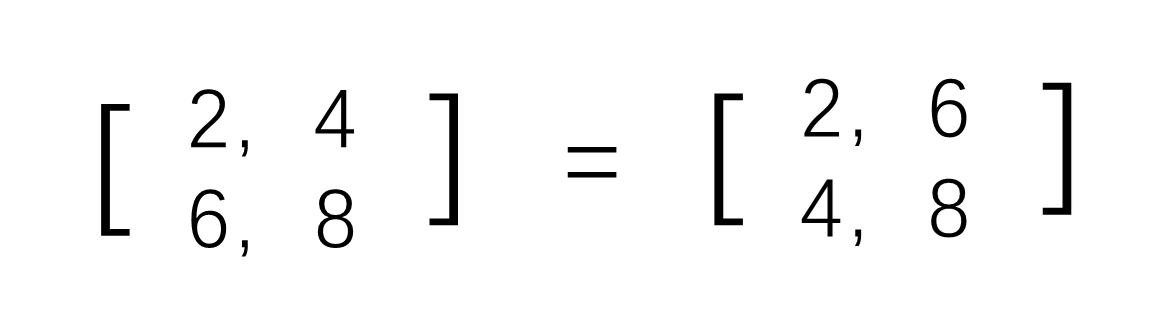基于消失点的相机自标定
附赠最强自动驾驶学习资料:直达链接
相机是通过透视投影变换来将3D场景转换为2D图像。在射影变换中,平行线相交于一点称之为消失点。本文详细介绍了两种利用消失点特性的标定方法。目的是为根据实际应用和初始条件选择合适的标定方法提供一个实用的工具。这里详细介绍了两种不同消失点的方法进行相机标定,并进行了比较。首先,利用合成数据对这两个模型进行了分析。最后,对每种方法进行了实际标定结果进行测试,结果证明了标定的质量。
主要内容
当我们在使用相机实现三维重建或者虚拟现实等交互场景时,需要对相机进行校准或者称之为标定。常见的比如三维重建、目标检测、场景建图和物体重建或自定位等任务都需要对场景进行标定。仅仅捕捉图像是不够的。显式相机标定是指标定过程以一组物理参数结束,获得一个详细的模型,尽可能接近真实系统的完整描述。Salvi等人发表了一份相机校准方法与精度评估的对比评论。这项调查的一个显著优点是,它标准化了符号,便于比较著名的标定方法,如Tsai、Hall或Faugeras。后来Zhang、Chen[5]或Heikkila对所提出的模型进行了改进。最常见的相机模型是针孔相机,它通过从三维欧几里德空间到图像平面的投影变换来生成图像。假设一个理想的投影中,点的共线保持不变。因此,场景中的线作为线投影到图像平面上。射影空间的一个有趣的特性是平行线相交于图像上的一个点,这与我们熟悉的欧几里德空间中平行线从不相交的情况不同。所以我们我们可以说在射影空间下,平行线的交点位于无穷远处,它在图像像平面上的投影称为消失点(VP)。
在本文中,我们将使用简短的符号VPs来表示属于正交方向的消失点。人们提出了许多方法来精确检测VPs。VPs的特性直接与焦距和相机相对于世界坐标系的旋转有关。Caprile和Beardsley是最早使用VPs估计相机内部参数的公司之一。后来,Hartley和Zisserman、Cipolla等人或He使用VPs来计算相机参数。两个类似的工作提出了一种利用从包含两个vp的多幅图像中获得的calibration sphere来寻找本征参数的方法。作者解释了用于提取校准矩阵的绝对二次曲线图像与calibration sphere之间的关系。
这里我们知道射影变换由齐次坐标的非奇异线性变换组成:
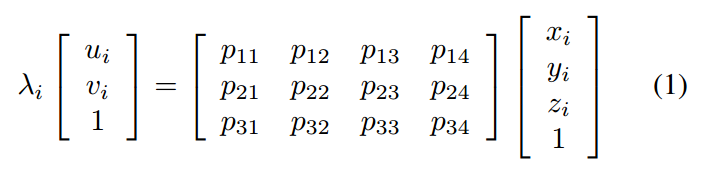
单应性矩阵P3×4,又称投影矩阵,可分解为相机内参矩阵与世界坐标系到相机机坐标系的变换矩阵的乘积:

针孔相机的通用模型考虑了两个像轴之间的倾斜系数,用γ表示,以及纵横比,或者比例因子,用αu和αv表示。因此,摄像机矩阵K的形式如下:
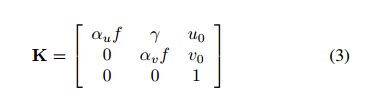
然而,通常采用的简化方法是将倾斜度设为零(γ=0),比例因子等于1,即αu=αv=1。构成旋转和平移矩阵的六个外部参数是对应于每个正交轴的三个旋转和三个平移。当内外参数确定后,对摄像机进行标定。
这里提出两种利用消失点特性的相机标定方法。Guillou等人提出的第一种方法只使用两个消失点。第二种方法由Cipolla等人提出,它使用三个消失点来确定摄像机模型的七个参数。两种方法产生的模型最初用于建筑物场景模型。(因为建筑物能够方便的提取出三个轴方向的消失点)
用两个消失点标定相机
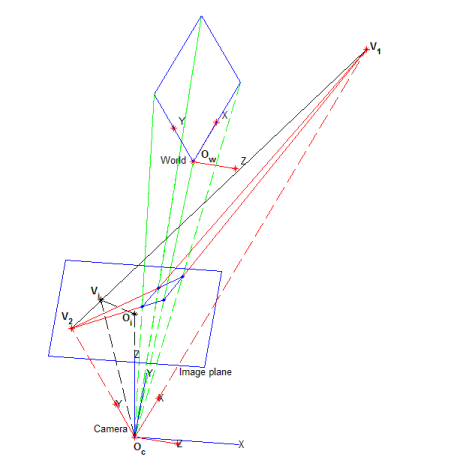
以两个坐标系为中心。将摄像机投影中心置于Oc处,图像的中心用Oi表示,Oc为在像面上的正交投影。设两个消失点V1和V2为世界坐标系的两个轴xw和yw的消失点,如图1所示。消失点在图像平面上的坐标是V1=(v1i,v1j)和V2=(v2i,v2j)。Oi在直线(V1V2)上的投影用Vi表示,主点位于光轴与像面相交处。其位置对于校准过程中的进一步计算至关重要。假设主点位于图像中心,纵横比等于1,即αu=αv=f,则只需使用两个消失点,就可以通过几何关系获得相机的内参和外参(这里有一个强制的假设主点位于图像的中心)
内参计算
图像中心被认为与主点重合。因此,它的坐标(u0,v0)立即获得。考虑Oc和Oi是沿光轴线的,可以计算焦距f,如上图所示,得到:
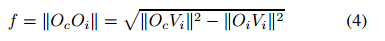
这里,OiVi是从图像中心到地平线的距离,由两个消失点计算可得
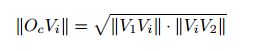
外参计算
世界坐标系和摄像机坐标系之间的旋转用矩阵R表示,考虑到两个消失点V1和V2在世界参考系的两个正交轴的方向上,以Ow为中心,所有平行线在一个消失点相交,我们可以建立一个矢量关系
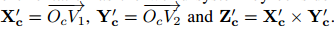
与世界系统具有相同的方向。因此,新坐标系和相机坐标系之间的旋转与世界坐标系和相机坐标系之间的旋转相同。向量X′c,Yc′,Z′c为:
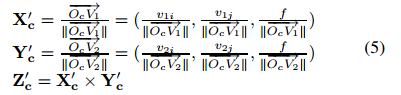
最终的旋转矩阵R可得:
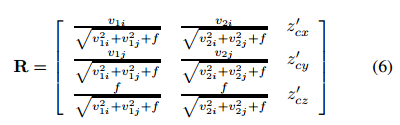
相机校准的最后一步是计算平移向量t。假设我们已知场景中已知长度的一小段,其两个端点中的第一个位于世界原点。在不失概括性的情况下,世界的中心可以在场景中的任何一点上选择。线段由世界点P1=[0,0,0]T和P2=[xp2,yp2,zp2]T确定,如下图所示。
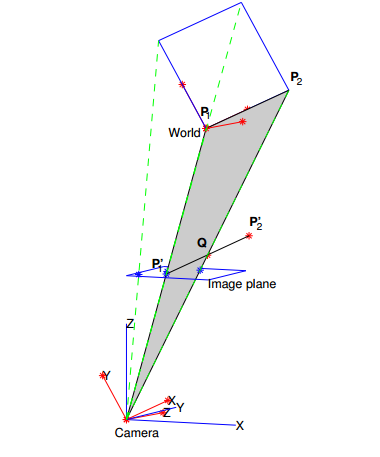
由于旋转矩阵R已知,我们可以将线段与其在相机坐标系中的图像对齐:
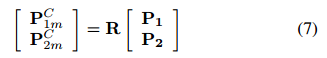
现实世界的线段由相机通过投影变换成像,产生两个图像点pi1px和pi2px,以像素表示。在针孔模型中,可以通过不做像素变换来计算图像中任何点的公制坐标,则第三个坐标是焦距:
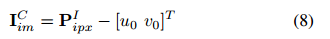
现在可以在图像平面上进行线段平移,方法是将其第一个点设置在其图像PI1m上并计算第二个点的位置。因此,平移后的线段由点P′1和P′2表示:
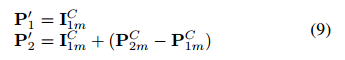
由此得到的△p1′p2与图中的两个三角形p1′Q平行。利用相似三角形的性质,我们可以得到:
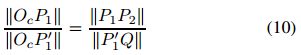
因此,从相机中心到世界中心的距离D可以计算为:
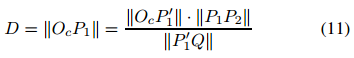
那么平移矩阵可得
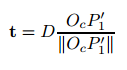
用三个消失点标定相机
该方法使用了从场景中正交方向确定的三个vp。假设图像中的三个消失点可以由已知的图像确定,例如两个正交的方格图案。本文不讨论非结构化场景中的VPs检测方法,因为这一主题超出了本文的主题。
内参计算
在当前的方法中,我们认为主点位于图像的中心,倾斜度为零(γ=0),比例因子等于1,即αu=αv=f。因此,相机矩阵具有简化形式:
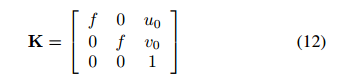
当图像大小已知时,直接确定主点的位置。唯一需要计算的固定参数是焦距。通过以下单应性,将三个相互正交方向对应的消失点投影到图像平面上:
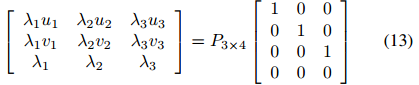
这三个消失点可以用比例来表示为:
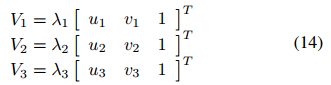
考虑到投影矩阵的分解,如等式(2)所示,可得:
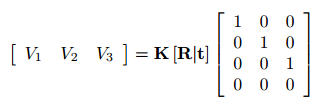
考虑到无穷远处齐次点与平移向量相乘的影响,我们得到:
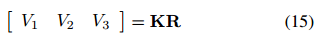
使用相机矩阵K,旋转矩阵R可以写成
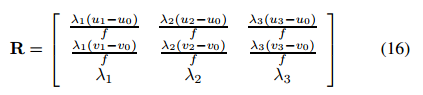
利用旋转矩阵的正交性,并将其应用于前两列,我们得到
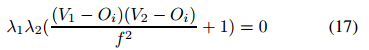
那么焦距可以计算如下
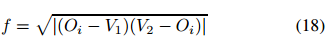
外参计算
外部参数是旋转矩阵R和平移向量t的一部分。如果确定了尺度因子λi,则可以计算方程中给出的旋转矩阵。为了计算它们,可以通过分离比例因子λi并使用无穷远处的齐次点与平移向量相乘来重新排列方程:
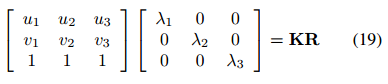
将两边的方程乘以(KR)T,并考虑旋转矩阵的正交性约束,得到:
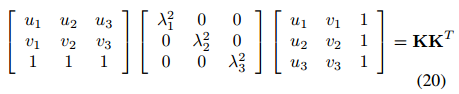
这里定义Q矩阵为
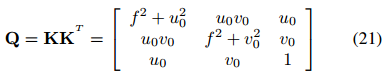
包含尺度因子λi的向量可以通过重新排列方程(20)和(21)来分离得到:
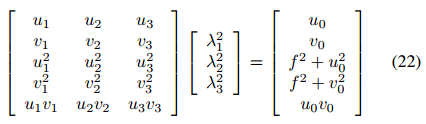
尺度因子可以通过方程组(22)上的奇异值分解来计算,并且可以确定旋转矩阵。注意,如果尺度因子已知,则确定方程(20)的左侧,并且可以通过在等式(21)中计算其值来直接计算固有参数。
当从场景中得到相互正交的方向的三个消失点时,可以使用另一种方法计算主点(u0,v0)的坐标,方法是找到由消失点形成的三角形的正交中心。平移向量t是从摄像机原点指向世界原点的向量,由投影矩阵的最后一列给出。世界坐标系的投影是从等式(1)中获得的,设定随机选择的原点的值Xi=0,Yi=0,Zi=0。在没有场景附加信息的情况下,从单个视图获得的平移将达到比例,其中λi具有任意值。如果有附加信息,如线段的长度或场景中点的坐标,则可以精确地提取平移矢量。设Ri为旋转矩阵的第i行,并且PWI=(X,Y,Zi,1)T是场景的点,投影到图像平面上
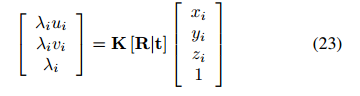
然后,得到以下方程组:
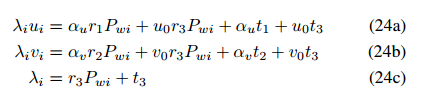
变换后得到
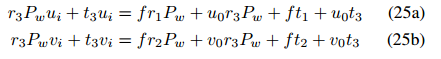
重新书写如下
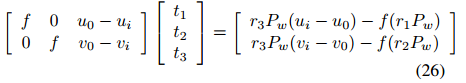
平移向量的分量可以通过叠加多对图像和场景点的方程(26)来计算,并使用奇异值分解来求解得到。寻找三个消失点需要至少六个点,放置在场景中三个相互正交的轴上,这些点也可以用于计算平移向量。
实验结果
为了研究所实现方法对噪声的鲁棒性,我们进行了一系列实验。在合成环境中工作的优点是可以获得绝对的地面真实值。在真实场景中,噪声通常存在于图像层面,因此,高斯噪声逐渐被加入到图像中,并利用受影响的图像对相机进行标定。在知道VPs的位置后,可以使用前面介绍的标定方法来估计相机模型。这一步是为了增加高斯噪声水平而反复进行的。为了获得尽可能接近每个方法的典型行为的结果,已经进行了50次迭代。通过计算图像、内参数和外参数三种输出的误差,测量了噪声对标定模型的影响。图像误差计算为参考点和重新投影点之间的距离。比较了摄像机的内参数αu和αv以及外部参数,即摄像机与世界参考系之间的旋转和平移。