文章目录
- 1. 最长递增子序列的个数
- 题干:
- 算法原理:
- 1. 状态表示:
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码:
- 2. 最长数对链
- 题干:
- 算法原理:
- 1. 状态表示:
- 2. 状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 代码:
- 3. 二叉搜索树中第 k 小的元素
- 算法原理:
- 代码:
- 4. 二叉树的所有路径
- 算法原理:
- 代码:
1. 最长递增子序列的个数

原题链接
题干:
给定一个未排序的整数数组 nums , 返回最长递增子序列的个数
注意 这个数列必须是 严格 递增的

算法原理:
1. 状态表示:
len[i] 表示:以ì位置元素为结尾的所有的子序列中,最长递增子序列的 “长度”
count[i] 表示:以i位置元素为结尾的所有的子序列中,最长递增子序列的 “个数”
2. 状态转移方程
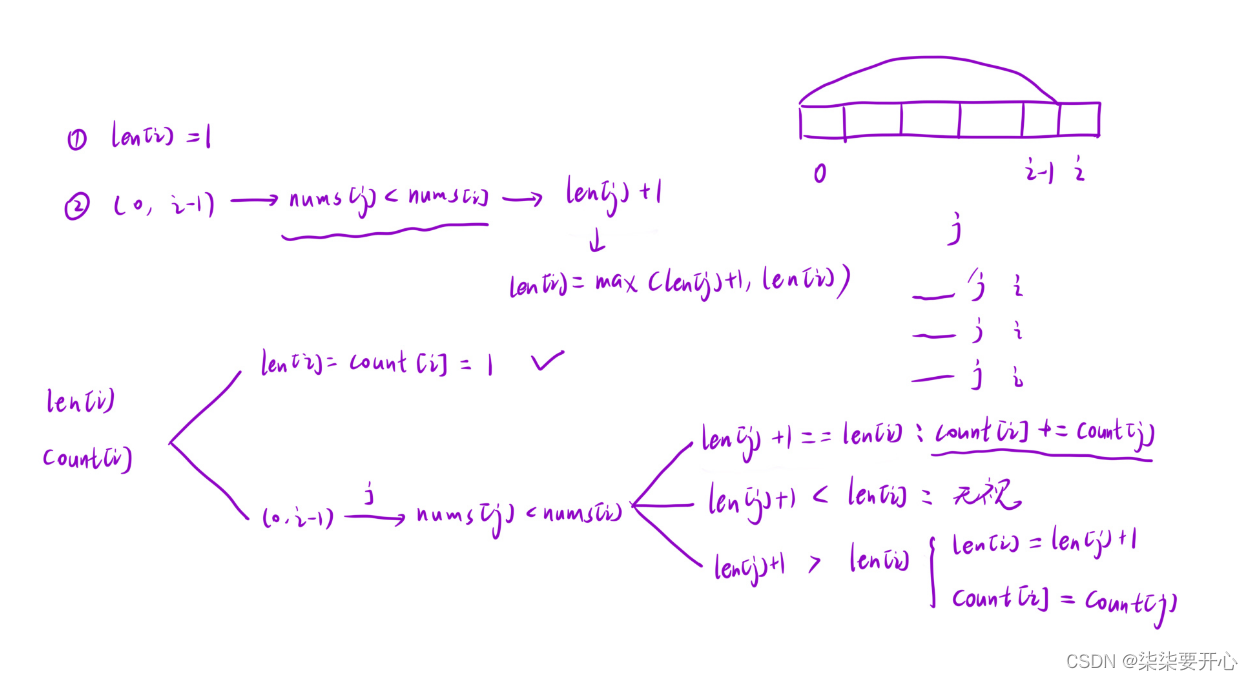
3. 初始化
两个表都初始化为 1
4. 填表顺序
从左往右
5. 返回值
小贪心
代码:
class Solution {public int findNumberOfLIS(int[] nums) {int n = nums.length;int[] len = new int[n];int[] count = new int[n];for(int i = 0; i < n; i++) {len[i] = count[i] = 1;}int retlen = 1;int retcount = 1;for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[j] < nums[i]) {if(len[j] + 1 == len[i]) {count[i] += count[j];}else if(len[j] + 1 > len[i]) {len[i] = len[j] + 1;count[i] = count[j];}}}if(retlen == len[i]) {retcount += count[i];}else if(retlen < len[i]) {retlen = len[i];retcount = count[i];}}return retcount;}
}
2. 最长数对链

原题链接
题干:
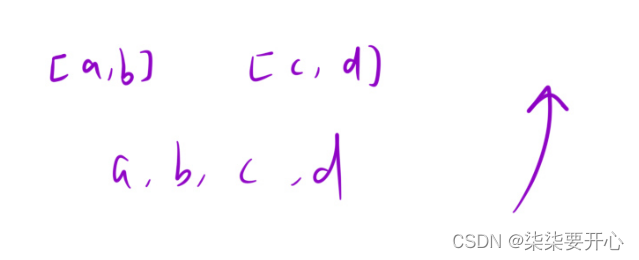
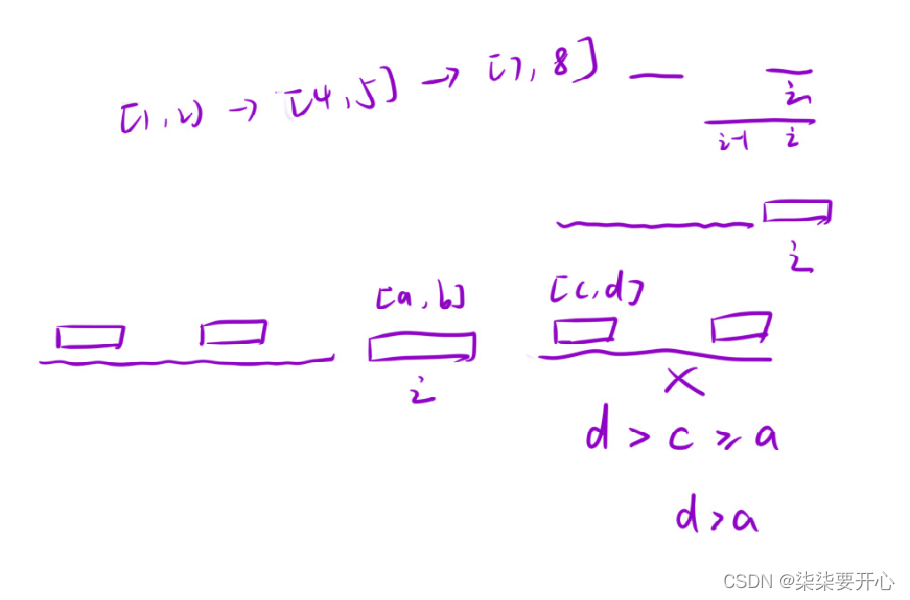
算法原理:
预处理,按第一个元素排序即可
1. 状态表示:
dp[i] 表示:以i位置元素为结尾的所有数对链中最长的数对链的长度
2. 状态转移方程
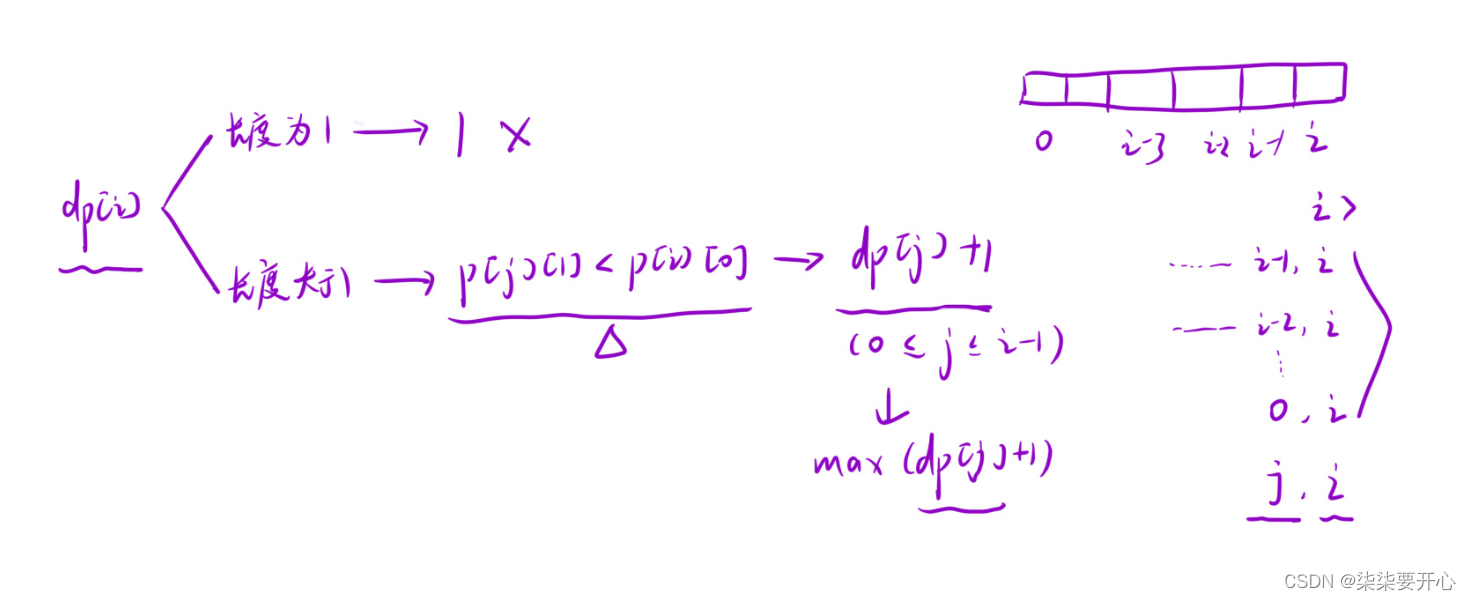
3. 初始化
全部初始化为 1
4. 填表顺序
从左往右
5. 返回值
表中的最大值
代码:
class Solution {public int findLongestChain(int[][] pairs) {Arrays.sort(pairs, (a, b) -> a[0] - b[0]);int n = pairs.length;int[] dp = new int[n];for(int i = 0; i < n; i++) {dp[i] = 1;}int ret = 1;for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(pairs[j][1] < pairs[i][0]) {dp[i] = Math.max(dp[j] + 1, dp[i]);}}ret = Math.max(ret, dp[i]);}return ret;}
}
3. 二叉搜索树中第 k 小的元素
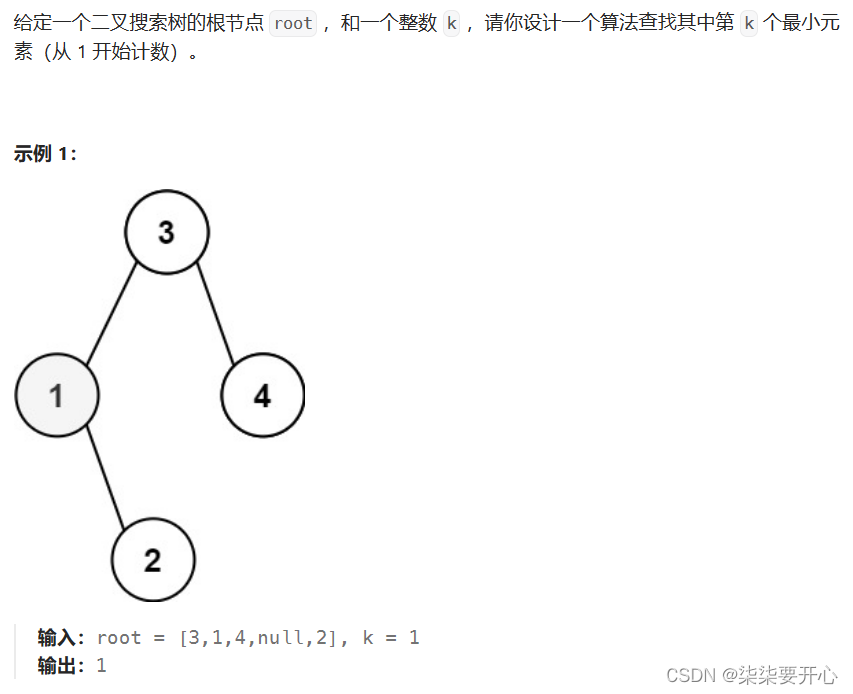
原题链接
算法原理:
使用两个全局变量 + 中序遍历
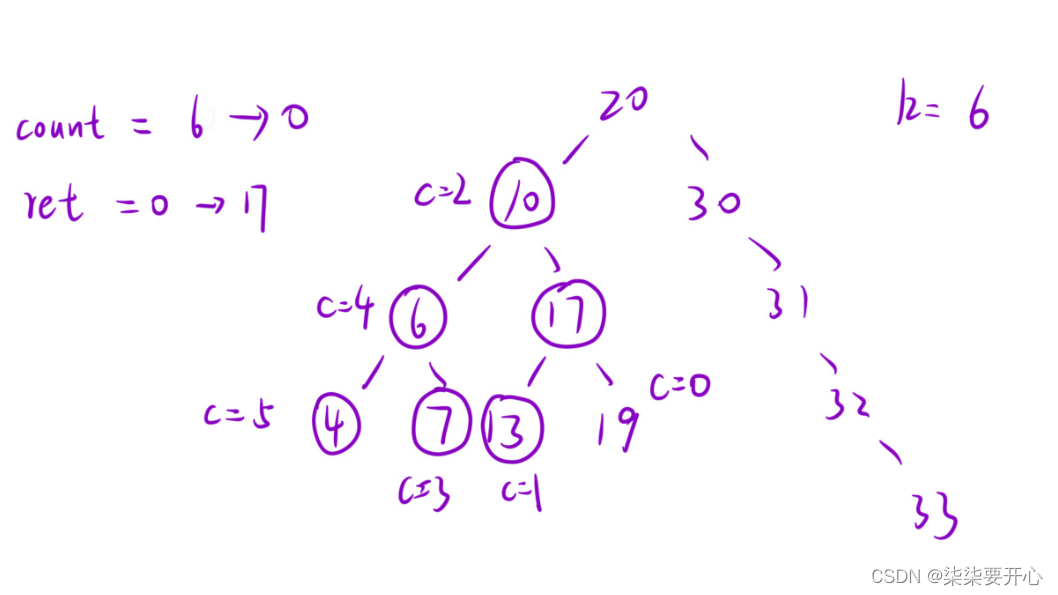
剪枝优化
代码:
class Solution {int count;int ret;public int kthSmallest(TreeNode root, int k) {count = k;dfs(root);return ret;}void dfs(TreeNode root) {if(root == null || count == 0) {return;}dfs(root.left);count--;if(count == 0) {ret = root.val;}if(count == 0) {return;}dfs(root.right);}}
4. 二叉树的所有路径
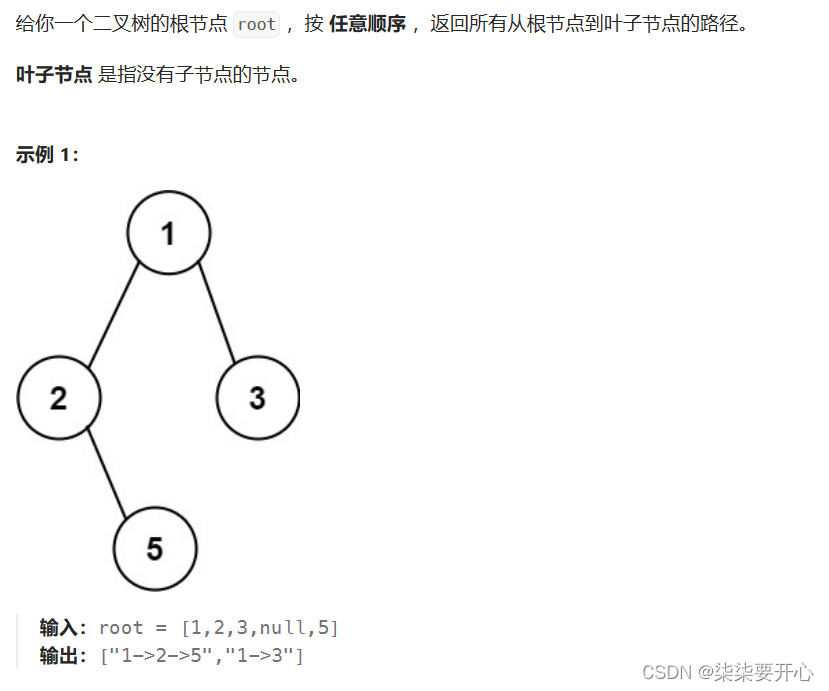
原题链接
算法原理:
- 使用全局变量
- 利用回溯 来 “恢复现场”
- 剪枝
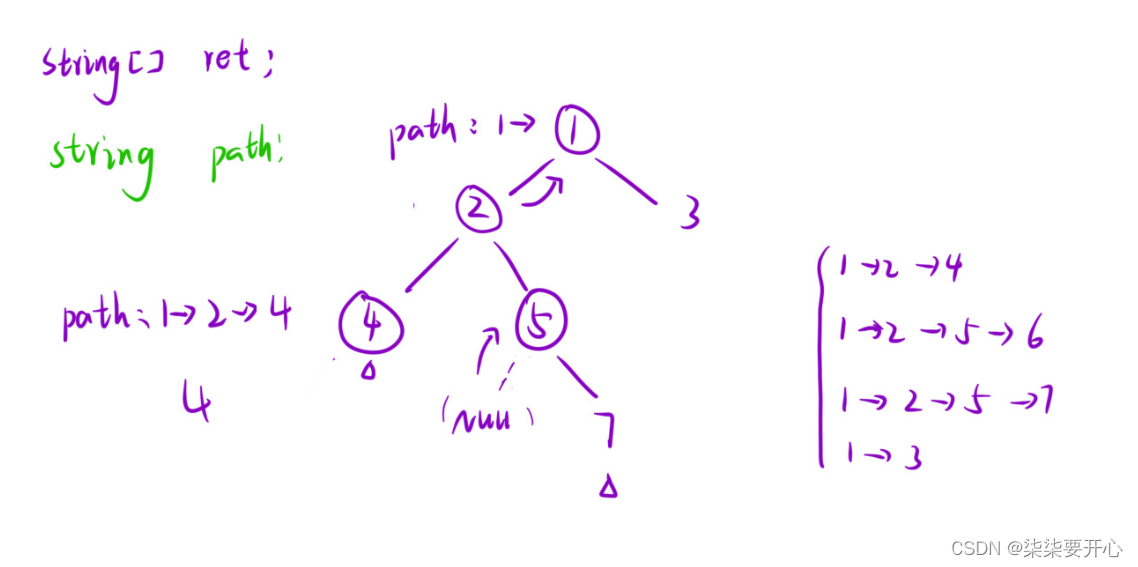
函数头:
void dfs(root, path)
函数体:
if(root == 叶子节点)
root != 叶子节点
递归出口:
if(toot == null)
return;
代码:
class Solution {List<String> ret;public List<String> binaryTreePaths(TreeNode root) {ret = new ArrayList<>();dfs(root, new StringBuffer());return ret;}void dfs(TreeNode root, StringBuffer _path) {StringBuffer path = new StringBuffer(_path);path.append(Integer.toString(root.val));if(root.left == null && root.right == null) {ret.add(path.toString());return;}path.append("->");if(root.left != null) {dfs(root.left, path);}if(root.right != null) {dfs(root.right, path);}}
}