目录
问题现象:
问题分析:
拓展:
1、除法运算:
拓展:MySQL中常用的几种除法运算
1、取整除法
2、浮点数除法
3、取余除法
4、向上取整除法
5、向下取整除法
2、运算结果的精度处理
1.1、浮点数
1.2、总位数
1.3、小数点后几位数
总结:
拓展:不要滥用cast句式
3、除数为0的处理
3.1、在程序中处理
3.2、sql中赋值为0
解决方法:
问题现象:
今天在项目中遇到一个需求是需要开发一个用到数据统计的接口,那么就有可能需要使用sql语句来进行除法运算;那么如何解决mysql中除法运算的以下2个问题呢:
1、运算结果的精度处理;
2、除数为0的处理。
问题分析:
首先,在进行数据统计相关的开发时,一般都会采用接口开发或定时任务统计这两种情况;而数据的统计逻辑一般有两种方式:
1、在数据库中进行简单运算,并将运算结果集返回给后端的dao层接口;
2、从数据库获取数据,然后在后端程序中做数据统计逻辑;
如果是简单的运算的话,可以采用第1种方式;而如果是需要进行大量复杂运算的话,建议采用第2种方式,如果你不确定的话也使用第2种方式,因为程序中可以很方便地实现简单运算,能完全兼容第1种方式,优点是可以定义各种变量来存储运算中的过程值;而第1种方式则适用于输出简单的运算结果。
拓展:
当然,我们都知道在数据库中,其实也可以使用存储过程(可以理解为后端服务中的函数\方法),来实现类似于后端程序的复杂运算逻辑,但是使用存储过程比使用后端程序的效率要低,所以不建议使用数据库的存储过程代替后端程序的方式来实现数据统计逻辑。
由于我这里需要做的是简单的除法运算,因此我想采用第1种方式来实现,那么现在就来分析一下文章开头提出了两个问题:
1、除法运算:
MySQL中作除法运算有很多种,其中最简单且常用的就是直接使用除法运算符(/);这种除法的特点是:运算结果是个浮点数。
例如:
select 10/5;
-- 结果:
-- 2.0000select 10/6;
-- 结果:
-- 1.6667可以发现:这种除法运算的默认规则就是:
小数点后保留4位数,且采用四舍五入的规则。
拓展:MySQL中常用的几种除法运算
MySQL中的除法运算有以下几种:
1、取整除法
MySQL旧版本:
DIV(被除数, 除数)MySQL新版本:
被除数 DIV 除数这里需要注意的一点是:上面列出了在MySQL中新旧版本下的DIV句式的使用规则,如果版本不对就会报错,这里由于我用的版本是MySQL8+,算是新版本,所以旧版本的句式不适用,所以就会报错如下:

所以如果报错的话,就换另一种句式试试吧。这里我只测试MySQL8+下成功的句式规则: 例如:

2、浮点数除法
运算结果是浮点数格式,默认是小数点后保留4位数,且采用四舍五入的规则。
例如:

3、取余除法
取运算结果的余数,也就是在除不净时余下的数值。
例如:

4、向上取整除法
得出运算结果后,先取整数部分;然后如果小数部分数值 > 0,则整数部分+1作为最终返回的结果。
例如,10/3=3.333...3;由于结果是个处于整数3和整数4之间的浮点数,所以向上取整,结果为:4。
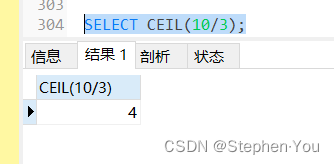
5、向下取整除法
得出运算结果后,取整数部分。
例如,10/3=3.333...3;由于结果是个处于整数3和整数4之间的浮点数,所以向下取整,结果为:3。

2、运算结果的精度处理
在mysql中可以使用以下句式来控制一个浮点数的精度:
cast(浮点数 AS DECIMAL(总位数, 小数点后几位数))这个句式需要用到3个参数:
1.1、浮点数
传入你想要操作的浮点数数据,在select...from语句中可以指定某个表的字段。
1.2、总位数
总位数指的是运算结果(浮点数)的总位数,分为两部分:小数点后数值的位数之和,所以总位数=小数点前数值的位数+小数点后数值的位数,这个总位数一定要设置的大一些,否则很容易踩坑的,后面我会提到。
1.3、小数点后几位数
对于运算结果,设置保留小数点后的几位数,也就是数学中常说的精确到小数点后几位数(精度)。
总结:
这个句式理解起来和用起来都很简单,唯一需要注意的点就是总位数的设置,这个数据必须设置大一些,尽量靠近数据的上限长度(浮点数的总位数最大值),我一般会设置30。
如果总位数设置太小,会导致数据失真,容易导致严重的数据问题。
例子:
select cast(1234567890.1234567890 AS DECIMAL(30, 4));
-- 结果:
-- 1234567890.1235select cast(1234567890.1234567890 AS DECIMAL(14, 4));
-- 结果:
-- 1234567890.1235select cast(1234567890.1234567890 AS DECIMAL(10, 4));
-- 结果:
-- 999999.9999select cast(1234567890.12 AS DECIMAL(10, 4));
-- 结果:
-- 999999.9999通过观察上面这4个sql语句的执行结果,不难看出,当总位数 < 浮点数的总位数最大值时,数据就会出现“失真”现象,即:
浮点数 > 总位数所能容纳的最大浮点数值,此时会直接返回该规则下的最大值,所以就能看到后面两个sql返回的结果是10个9(小数点后4个+小数点前6个);规则是首先满足小数点后有4位数,然后再从小数点往前取6位数,来凑够10位数字,以达到我们设置的总位数。
拓展:不要滥用cast句式
这里有一个需要注意的点,就是不要滥用cast句式,我们只需要对最终的运算结果做精度设置即可,千万不要画蛇添足地给被除数和除数都做精度设置,否则就会出现以下这种情况:

可以发现,我们给被除数和除数都设置了精度时,会把两个精度相加【(5,4)+(5,4)=(10,8)】作为运算结果的精度。我们可以分析一下这个结果是怎么得出来的:
第一步先执行:

得出真正的被除数:9.9999
第二步执行:
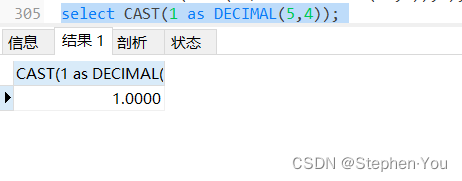
得出真正的被除数:1.0000
第三步把两个精度加起来作为最终结果的精度规则并做除法运算,相当于:
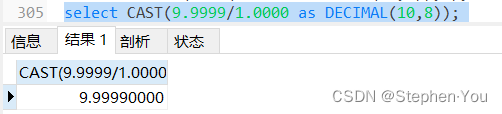
而正确的sql应该是:
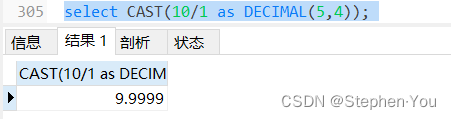
由于总位数不够设置太小,导致失真,所以需要增大总位数:

3、除数为0的处理
我们都知道,在除法运算中除数不能为0;
但神奇的是:在MySQL中使用到除数为0的除法运算,是不会报错,但是返回的运算结果是Null;

那么如果除数为Null呢?

还是没报错,但返回的运算结果还是Null;
但做过数据统计的小伙伴应该都知道:统计数据的报表中不会显示为null,而需要显示为0、0.0、0%等等,因此当除数为0时,这里提供有两种处理方法:
3.1、在程序中处理
当数据库返回的运算结果为null,程序中判断后即可对其做针对性处理,如报错,或者赋值为0等等。
3.2、sql中赋值为0
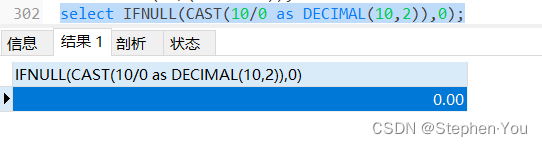
在MySQL中使用IFULLl句式进行处理,返回运算结果0,如下:

解决方法:
除法运算精度和除数为0的综合处理:
先设置精度,再处理0: