💕"深思熟虑的结果往往就是说不清楚。"💕
作者:Mylvzi
文章主要内容:算法系列–动态规划–子序列(2)
今天带来的是
算法系列--动态规划--子序列(1),是子序列问题的开篇!带大家初识子序列问题
一.什么是子序列问题
我们之前已经学习过子数组问题,子数组问题最大的特点就是求一段连续区间的xxxx,子数组问题的经典的状态表示就是以i位置为结束,xxxx,推导状态转移方程的一个经验是根据数组的结构来区分不同的结构
子序列问题本质上是对子数组问题的一个拓展,或者说子序列问题包含了子数组问题
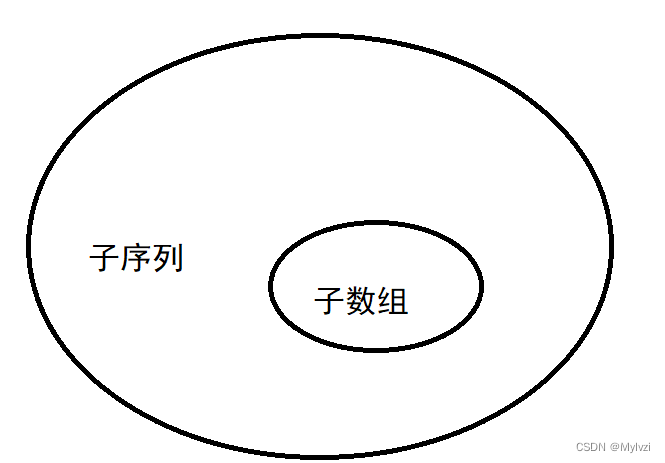
子序列问题相较于子数组问题最大的不同在于序列可以是不连续的,也就是序列既可以连续又可以不连续,所以说子序列问题包含了子数组问题
但是子序列问题的状态表示和状态转移方程的推导方式和子数组问题十分相似!可以总结为以下步骤:
- 根据
经验,确定状态表示dp[i],这一步和子数组问题中的状态表示很像,往往都是根据题目的意思+经验确定状态表示 - 状态转移方程:子序列/子数组问题的状态转移方程的推导方式比较固定,既
按照构成子序列/子数组的形式确定,一般就分为两类
- 单独一个 nums[i]
- 前面一堆 + nums[i]
- 初始化:对于子序列问题来说,一般单独的一个数字也可以表示一种状态(1),1就表示
最次状态,所以往往将dp表初始化为1 - 填表顺序:不固定,但一般都是从左往右的线性表
- 返回值:具体问题具体分析
下面是一些经典问题:
二.子序列题目讲解
1.最⻓递增⼦序列
链接: 最⻓递增⼦序列
分析:
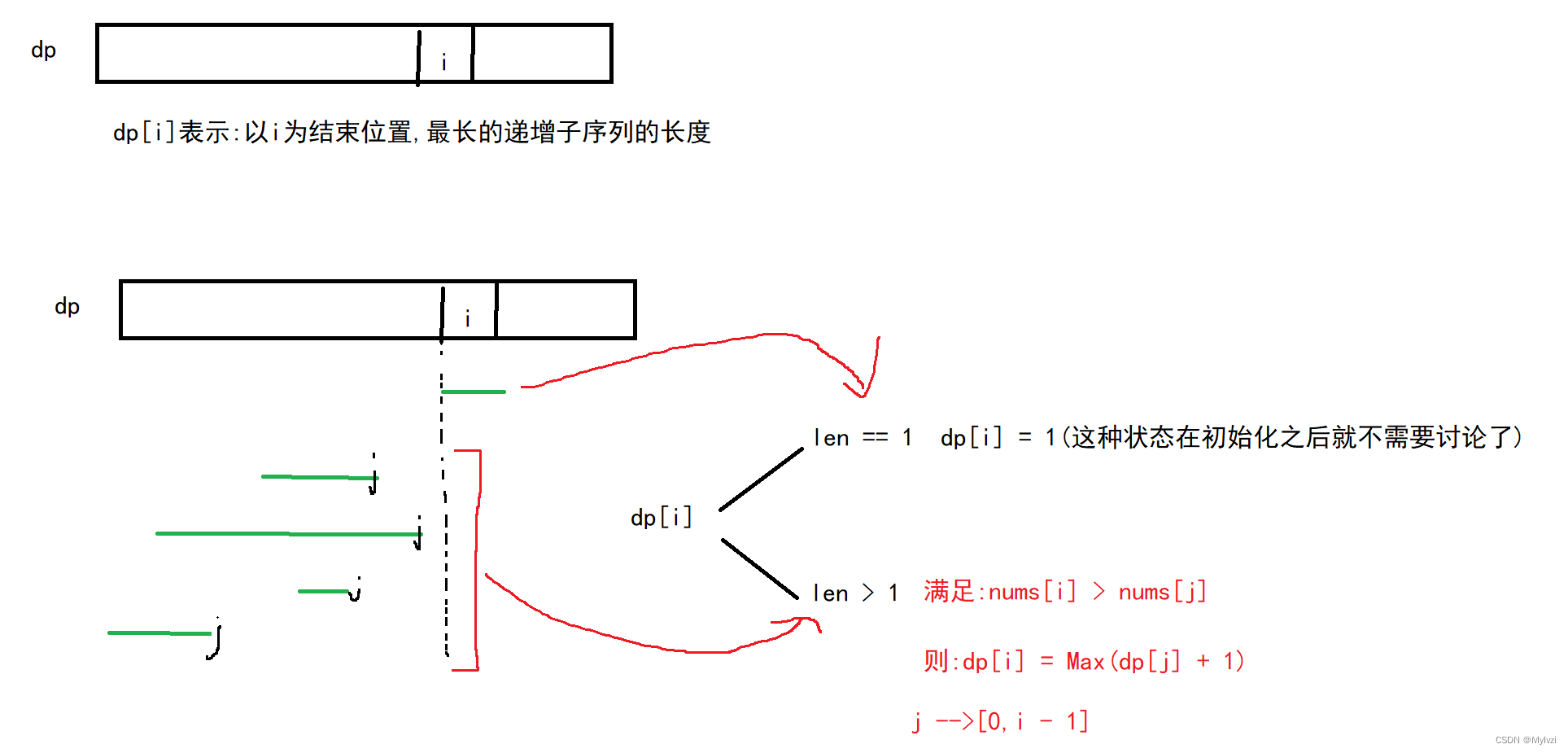
- 状态表示:dp[i]表示
以i为结束位置,最长的递增子序列的长度 - 状态转移方程:观察构成dp[i]的形式有两种,nums[i]
单独一个,此时dp[i]==1,第二种形式是和之前的任意一段子序列重新构成一个新的递增子序列,设前面子序列的结束位置为j,则dp[i] =Max(dp[j] + 1) - 初始化:由于一个nums[i]也可以组成一个子序列,所以最次的状态就是
1,进而可以将dp表初始化为1(这样也就可以不讨论状态转移方程中nums[i]单独一个的情况) - 填表顺序:从左至右
- 返回值:返回
dp[i]的最大值
代码:
class Solution {public int lengthOfLIS(int[] nums) {int n = nums.length;int[] dp = new int[n];for(int i = 0 ; i < n; i++) dp[i] = 1;// 初始化dp表int ret = dp[0];// 记录最值// 填表for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[i] > nums[j])// 注意不是任何一个子序列都可以和nums[i]构成严格递增的子序列的 必须符合条件dp[i] = Math.max(dp[j] + 1,dp[i]);}ret = ret > dp[i] ? ret : dp[i];}return ret;}
}
注意:
子序列问题相较于子数组问题的解题过程多了一层for循环,正是因为子序列问题的不连续的特性,所以要遍历i位置之前的所有子序列,时间复杂度相较于子数组问题也更高
2.摆动序列
链接:摆动序列
分析:
-
状态表示:根据经验很容易想到这道题的状态表示是以i位置为结束的摆动序列的最长子序列的的长度,但是在分析接下来的状态转移方程时,发现dp[i]的状态是收到
前一个数的差值的正负所影响的,如果前面的差值是负,则nums[i]与前一序列结尾的数字nums[j]的差值必须为正,反之依然,所以仅仅通过一个状态转移方程是不够的,我们需要创建出两个状态转移方程表f[i]:以i位置为结尾,nums[i]与nums[j]的差值为正的最长子序列的长度
g[i]:以i位置为结尾,nums[i]与nums[j]的差值为负的最长子序列的长度
2.状态转移方程:
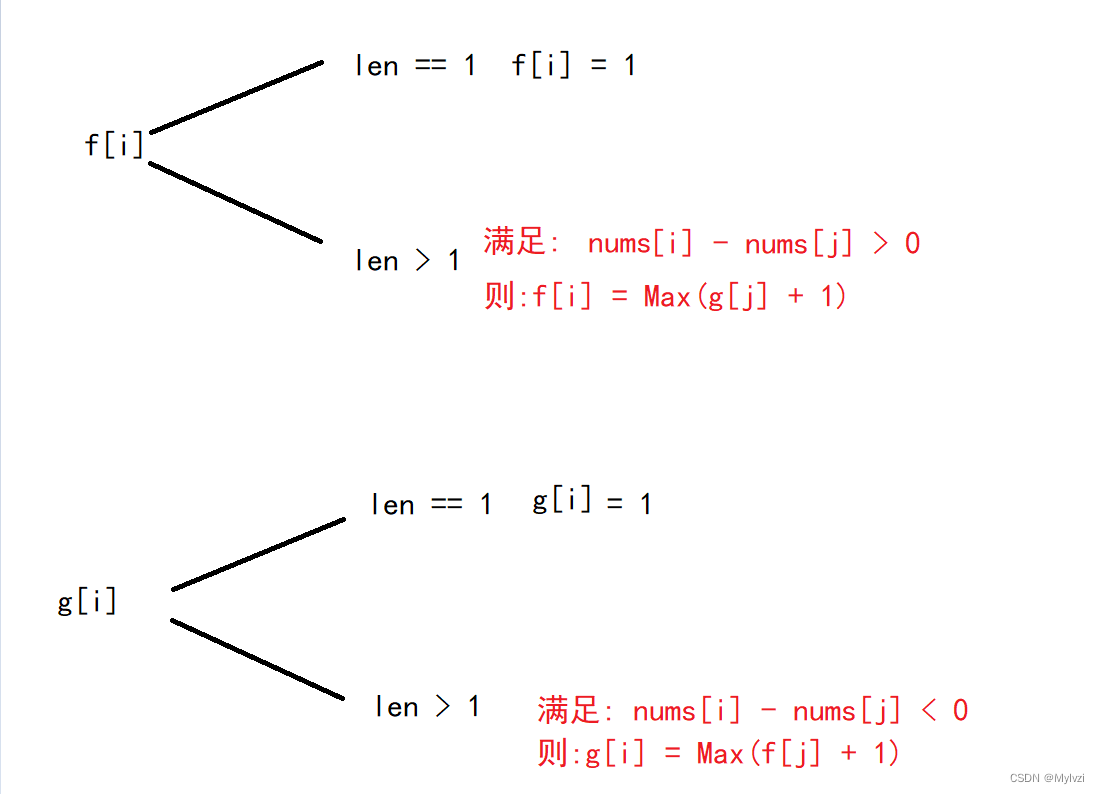
- 初始化:最次状态为1,所以两个表都初始化为1
- 填表:从左往右
- 返回值:两个表的最大值
代码:
class Solution {public int wiggleMaxLength(int[] nums) {int n = nums.length;int[] f = new int[n];// 差值为正数的dp表int[] g = new int[n];// 差值为负数的dp表for(int i = 0; i < n; i++) f[i] = g[i] = 1;int ret = f[0];for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[i] - nums[j] > 0) f[i] = Math.max(g[j] + 1,f[i]);else if(nums[i] - nums[j] < 0) g[i] = Math.max(f[j] + 1,g[i]);}ret = Math.max(f[i],g[i]);// 更新最大值}return ret;}
}
3.最长定差子序列
链接:最长定差子序列
分析:
- 笔者一拿到本题就想到了
最长递增子序列那道题目,只不过这里的增加的条件变为了nums[i] - nums[j] == difference,但是大致的过程是相同的,笔者兴冲冲的C,V结果发现超时(小丑了) - 优化策略:超时代码中时间复杂度最高的地方在于需要对j从0位置一直遍历到i - 1,再加上外层循环,时间复杂度达到
O(N^2),所以需要优化这里的寻找过程 - 这个寻找过程的目的是
找到最长的定差子序列,但是实际上没有必要从0开始找,如果有两个重复的nums[j],我们只需要取其中对应的dp[j]较大的值即可.而且,我们在遍历nums[i]的过程中,可以将每次遍历得到的nums[i]和dp[i]存入到哈希表之中,这样再回头去找最长的子序列时,只需寻找key = a - difference即可,这样搜索的时间复杂度就降低到O(1)
超时代码
class Solution {public int longestSubsequence(int[] nums, int difference) {int n = nums.length;int[] dp = new int[n];for(int i = 0 ; i < n; i++) dp[i] = 1;// 初始化dp表int ret = dp[0];// 记录最值// 填表for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[i] - nums[j] == difference)dp[i] = dp[i] > dp[j] + 1 ? dp[i] : dp[j] + 1;}ret = ret > dp[i] ? ret : dp[i];}return ret;}
}
优化:
class Solution {public int longestSubsequence(int[] arr, int difference) {Map<Integer,Integer> hash = new HashMap<>();int ret = 1;// 记录最值for(int a : arr) {hash.put(a,hash.getOrDefault(a-difference, 0 ) + 1);// 将当前位置插入到哈希表中ret = Math.max(ret,hash.get(a));// 更新最值}return ret;}
}
4.最长数对链
链接:最长数对链
分析:
- 本题其实和
最长递增子序列很像,只不过这里换成了数对,需要注意的是,本题的子序列是可以任意挑选的,所以需要对数组进行排序
代码:
class Solution {public int findLongestChain(int[][] nums) {// 预处理数组 --转化为子序列问题Arrays.sort(nums,(a,b) -> {return a[0] - b[0];});// 此处使用的lambda表达式// 下面的思路和"最长递增子序列长度"相同int n = nums.length;int[] dp = new int[n];for(int i = 0; i < n; i++) {dp[i] = 1;}int ret = dp[0];for(int i = 1; i < n; i++) {for(int j = 0; j < i; j++) {if(nums[i][0] > nums[j][1]) {dp[i] = Math.max(dp[i],dp[j] + 1);}}ret = ret > dp[i] ? ret : dp[i];}return ret;}
}