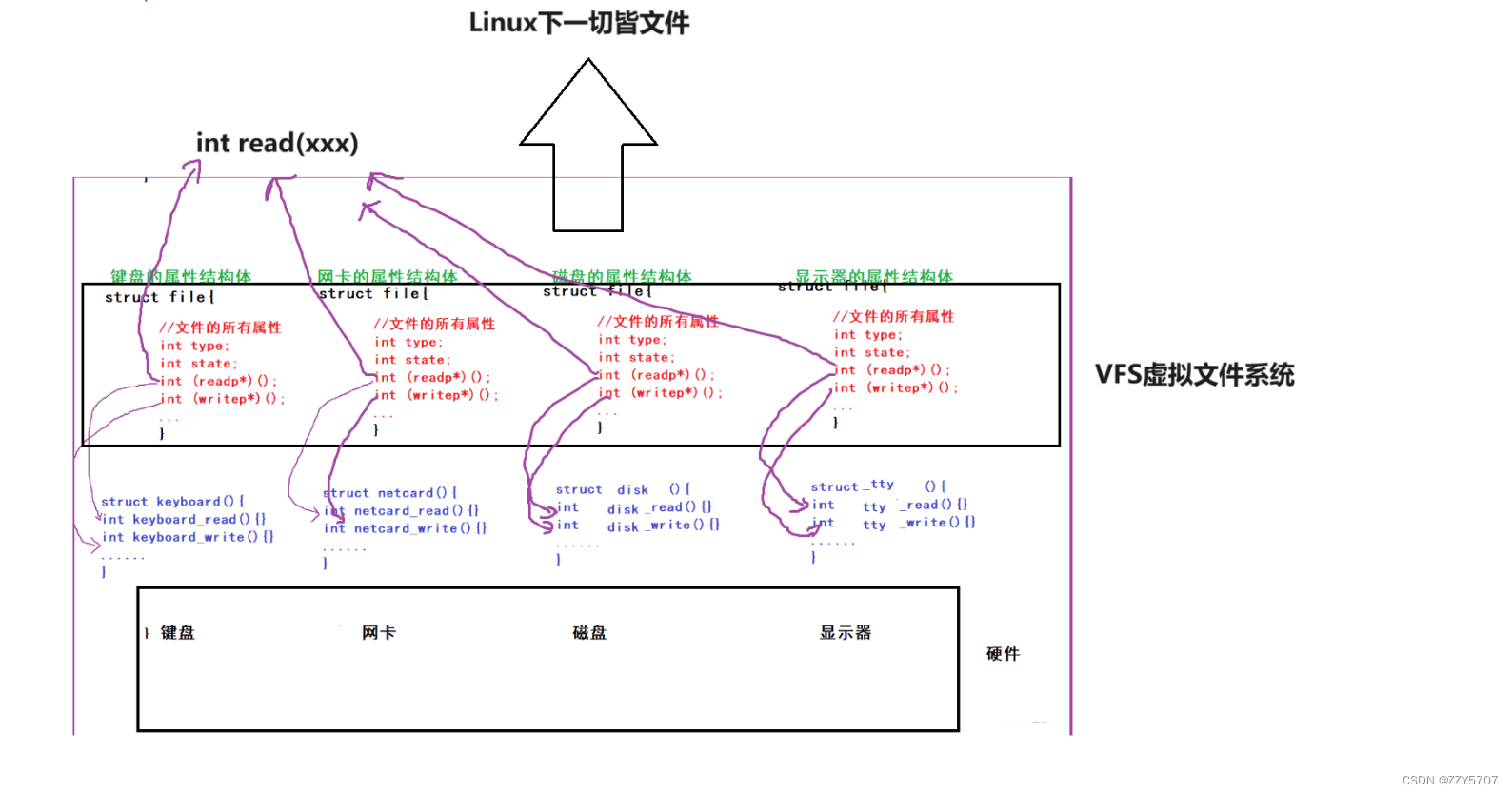
K均值聚类
- 1、引言
- 2、K均值聚类
- 2.1 定义
- 2.2 原理
- 2.3 实现方式
- 2.4 算法公式
- 2.4.1 距离计算公式
- 2.4.1 中心点计算公式
- 2.5 代码示例
- 3、总结
1、引言
小屌丝:鱼哥, K均值聚类 我不懂,能不能给我讲一讲?
小鱼:行,可以
小屌丝:额…今天咋直接就答应了?
小鱼:不然呢?
小屌丝:有啥条件,直接说,
小鱼:没有
小屌丝:这咋的了,不提条件,我可不踏实
小鱼:你看看你, 我不提条件,你还不踏实,那你这是非让我提条件呗
小屌丝:我…这…我…
小鱼:既然你都让我提条件了,那我就说吧
小屌丝: …
小鱼:最近好长时间没撸串了哈。
小屌丝:…

小鱼:你看看,让我提条件, 还这表情。那算了。
小屌丝:别别别, 可以可以。
小鱼: 这是,可以去吃,还是别提条件?
小屌丝:去撸串> <
2、K均值聚类
2.1 定义
K均值聚类是一种无监督学习算法,旨在将数据划分为K个不相交的簇,使得每个数据点都属于离其最近的簇的质心。
质心是每个簇中所有数据点的平均值,代表该簇的中心位置。
2.2 原理
K均值聚类的原理基于迭代优化。
- 算法首先随机选择K个初始质心,然后将每个数据点分配给最近的质心所在的簇。
- 接下来,算法重新计算每个簇的质心位置,即该簇内所有数据点的平均值。
这个过程不断重复,直到满足某个停止条件,如质心位置不再发生显著变化或达到最大迭代次数。
2.3 实现方式
K均值聚类的实现主要包括以下步骤:
- 初始化:随机选择K个数据点作为初始质心。
- 分配数据点到簇:对于每个数据点,计算其与所有质心的距离,并将其分配给最近的质心所在的簇。
- 更新质心:对于每个簇,重新计算其质心位置,即该簇内所有数据点的平均值。
- 重复迭代:重复步骤2和3,直到质心位置不再发生显著变化或达到最大迭代次数。
2.4 算法公式
2.4.1 距离计算公式
对于每个数据点,计算其与每个中心点之间的距离。常用的距离计算公式是欧氏距离公式:
d ( x , y ) = s q r t ( ( x 1 − y 1 ) 2 + ( x 2 − y 2 ) 2 + … + ( x n − y n ) 2 ) d(x, y) = sqrt((x1-y1)^2 + (x2-y2)^2 + … + (xn-yn)^2) d(x,y)=sqrt((x1−y1)2+(x2−y2)2+…+(xn−yn)2)
其中, x x x和 y y y分别表示两个数据点的特征向量, n n n表示特征的维度。
2.4.1 中心点计算公式
中心点更新公式: C k = ( 1 / ∣ S k ∣ ) ∗ Σ x i Ck = (1/|Sk|) * Σxi Ck=(1/∣Sk∣)∗Σxi
其中 C k Ck Ck为第 k k k个类别的中心点, S k Sk Sk为第 k k k个类别中的数据点集合。
2.5 代码示例
# -*- coding:utf-8 -*-
# @Time : 2024-03-13
# @Author : Carl_DJ'''
实现功能:实scikit-learn库实现K均值聚类'''
import numpy as np # 假设我们有一个二维数据集X
X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]]) # 设定簇的数量
K = 2 # 步骤1: 初始化质心
# 随机选择K个数据点作为初始质心
np.random.seed(0) # 为了可重复性设置随机种子
initial_centroids = X[np.random.choice(range(X.shape[0]), K, replace=False)]
centroids = initial_centroids # 迭代过程
max_iterations = 100 # 最大迭代次数
tolerance = 1e-4 # 收敛阈值
has_converged = False
iteration = 0 while not has_converged and iteration < max_iterations: # 步骤2: 分配数据点到簇 # 对于每个数据点,计算其与所有质心的距离,并将其分配给最近的质心所在的簇 labels = [] for x in X: distances = np.linalg.norm(x - centroids, axis=1) label = np.argmin(distances) labels.append(label) labels = np.array(labels) # 旧的质心位置,用于收敛性检查 old_centroids = centroids.copy() # 步骤3: 更新质心 # 对于每个簇,重新计算其质心位置,即该簇内所有数据点的平均值 new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(K)]) centroids = new_centroids # 步骤4: 检查收敛性 # 如果质心不再发生显著变化,则算法收敛 if np.allclose(old_centroids, centroids, atol=tolerance): has_converged = True iteration += 1 # 输出结果
print("Iterations:", iteration)
print("Labels:", labels)
print("Centroids:", centroids)代码解析
实现K均值聚类的完整过程:
-
初始化质心:通过np.random.choice随机选择K个数据点作为初始质心。
-
分配数据点到簇:对于数据集中的每个数据点,我们计算它与所有质心的距离,并将其分配给最近的质心所在的簇。这通过遍历数据点,计算每个点到所有质心的欧几里得距离,并找到最近的质心来完成。
-
更新质心:对于每个簇,我们计算该簇内所有数据点的平均值作为新的质心位置。这通过分组数据点(基于它们的簇标签)并计算每组的平均值来实现。
-
检查收敛性:我们检查新的质心位置是否与旧的质心位置非常接近(在容忍度范围内)。如果是,则算法已经收敛,可以停止迭代。否则,我们继续迭代过程。
-
重复迭代:如果算法没有收敛,我们重复步骤2到步骤4,直到达到最大迭代次数或算法收敛为止。

3、总结
K均值聚类是一种简单而有效的无监督学习算法,能够自动将数据划分为K个不同的簇。
通过迭代优化过程,算法将数据点分配给最近的质心,并重新计算质心位置,直到满足停止条件。
K均值聚类在数据处理、图像分割和模式识别等领域具有广泛的应用。
然而,它也有一些局限性,如对初始质心的选择敏感、可能陷入局部最优解等。
在实际应用中,需要根据具体任务和数据特点选择合适的算法和参数。
我是小鱼:
- CSDN 博客专家;
- 阿里云 专家博主;
- 51CTO博客专家;
- 企业认证金牌面试官;
- 多个名企认证&特邀讲师等;
- 名企签约职场面试培训、职场规划师;
- 多个国内主流技术社区的认证专家博主;
- 多款主流产品(阿里云等)测评一、二等奖获得者;
关注小鱼,学习机器学习领域的知识。