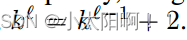迷宫（蓝桥杯）——DFS和BFS

迷宫

题目描述

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这 个它的上、下、左、右四个方向之一。

对于上面的迷宫，从入口开始，可以按 DRRURRDDDR 的顺序通过迷宫， 一共 10 步。其中
D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫（30 行 50 列），
请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。

请注意在字典序中 D<L<R<U。

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

答案

DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

暴力DFS

这段代码是一个迷宫求解程序，使用深度优先搜索（DFS）算法来找到从迷宫的左上角（起点）到右下角（终点）的最短路径。下面是对代码的详细注释：

#include<bits/stdc++.h>
using namespace std;// 定义列数和行数
const int col=30, row=50;// 迷宫的二维数组，0表示可通行，1表示障碍
int mp[col+1][row+1] = {// 迷宫的具体布局，这里省略了具体的数字，只给出了格式// ...
};// 用于记录路径的字符数组
char a[col*row];// 用于保存最终路径的字符串
string s;// 记录从起点到终点的最短步数
int best = INT_MAX;// 判断函数，用来判断当前坐标是否在迷宫内部且为可通行区域
int judge(int x, int y) {if (x > 0 && x <= col && y > 0 && y <= row && v[x][y] == 0 && mp[x][y] == 0)return 1;return 0;
}// 深度优先搜索函数，用于寻找路径
void dfs(int x, int y, int step) {// 如果当前步数已经超过已知的最短步数，则直接返回if (step > best)return;// 如果已经到达终点（迷宫的右下角），则记录路径if (x == col && y == row) {string temp;// 将路径中的每一步转换为字符串形式并拼接for (int i = 0; i < step; i++)temp += a[i];// 如果当前路径比已知的最短路径更短，则更新最短路径if (step < best) {best = step;s = temp;}// 如果当前路径与已知的最短路径同样短，但字典序更小，则更新最短路径else if (step == best && temp < s)s = temp;return;}// 定义四个可能的移动方向：上、下、左、右int dir_x[4] = {-1, 1, 0, 0};int dir_y[4] = {0, 0, -1, 1};char dir[4] = {'U', 'D', 'L', 'R'};// 遍历所有可能的移动方向for (int i = 0; i < 4; i++) {int x_1 = x + dir_x[i];int y_1 = y + dir_y[i];// 如果新的位置在迷宫内部且为可通行区域if (judge(x_1, y_1)) {// 记录当前方向到路径数组中a[step] = dir[i];// 标记当前位置为已访问v[x_1][y_1] = 1;// 递归调用dfs函数，继续搜索下一个位置dfs(x_1, y_1, step + 1);// 回溯，将当前位置标记为未访问v[x_1][y_1] = 0;}}
}int main() {// 将起点标记为已访问v[1][1] = 1;// 调用dfs函数开始搜索dfs(1, 1, 0);// 输出最终找到的最短路径cout << s << endl;// 输出最短路径的步数cout << best << endl;return 0;
}

这段代码的主要逻辑是通过深度优先搜索来遍历迷宫的所有可能路径，同时记录并更新最短路径。在搜索过程中，使用了一个二维数组 v 来标记已经访问过的位置，以避免重复访问。当到达终点时，会检查当前路径的步数是否比已知的最短路径更短，或者在步数相同的情况下是否字典序更小。如果满足条件，就会更新最短路径。最后，程序输出找到的最短路径及其步数。

因为dfs是遍历到每一条路径，所以代码编译时间一定很长，但这是填空题，所以暴力也是一种办法
在这里插入图片描述
所以，我们需要优化

这个方法好像不行，我运行4个小时也没出答案，应该是递归太多栈溢出了

DFS+剪枝优化

根据上面代码以及截图来看，如果我们定义一个mins数组来存储从起点到该点的位置，如果 pos+1 大于 mins[tox][toy]，那么当前路径不会是到达 (tox, toy) 的最短路径，因此没有必要继续在这个方向上搜索，可以剪枝，节省搜索时间。

因此，我们只需要在if判断中加入pos+1<=mins[tox][toy]条件即可

if(judge(tox,toy)&&pos+1<=mins[tox][toy])//判断下一步是否合法且如果pos+1大于起点到（tox，toy）的步骤，依然无意义

代码详细注释如下：

// 引入必要的头文件
#include<iostream>
#include<cstring> // 用于 memset 函数
#include<string> // 用于 string 类型
using namespace std;// 定义四个可能的移动方向：右（R）、左（L）、下（D）、上（U）
const int dirx[4] = {0, 0, 1, -1}; // x 坐标的变动
const int diry[4] = {1, -1, 0, 0}; // y 坐标的变动
const char dir[4] = {'R', 'L', 'D', 'U'}; // 方向的缩写// 定义迷宫的行数和列数
const int row = 30, col = 50;// 定义一个字符数组，用于记录最终的路径序列
char a[row * col + 5];// 定义一个字符串，用于存储最终的路径序列
string ans;// 定义迷宫数组，0 表示可通行，1 表示障碍
int maze[row + 1][col + 1] = {// 迷宫的具体布局，这里省略了具体的数字，只给出了格式// ...
};// 判断函数，用于检查坐标 (x, y) 是否在迷宫内部且为可通行区域
int judge(int x, int y) {if (x > 0 && x <= row && y > 0 && y <= col && maze[x][y] == 0)return 1;return 0;
}// 深度优先搜索函数，用于寻找通往出口的最短路径
void dfs(int x, int y, int pos) {// 如果当前步数已经超过已知的最短步数 best，则直接返回if (pos > best)return;// 如果已经到达终点（迷宫的右下角），则记录路径if (x == row && y == col) {// 根据路径记录构建字符串string temp;for (i = 0; i < pos; i++) {temp += a[i];}// 如果当前路径比已知的最短路径更短，则更新 best 和 ansif (pos < best) {ans = temp;best = pos;} else if (pos == best && temp < ans) {ans = temp;}return;}// 遍历四个可能的移动方向for (int i = 0; i < 4; i++) {int tox = x + dirx[i];int toy = y + diry[i];// 如果新的位置在迷宫内部且为可通行区域if (judge(tox, toy)) {// 标记当前位置为已访问maze[tox][toy] = 1;// 更新到新位置的最短步数mins[tox][toy] = pos + 1;// 记录移动方向到路径数组中a[pos] = dir[i];// 递归调用 dfs 函数，继续搜索下一个位置dfs(tox, toy, pos + 1);// 回溯，将当前位置标记为未访问maze[tox][toy] = 0;}}
}// 主函数
int main() {// 初始化 mins 数组，将所有值设置为一个非常大的数，表示无穷大memset(mins, 1, sizeof(mins));// 初始化 best 为一个非常大的数，用于记录从起点到终点的最小步数best = 1 << 28;// 将迷宫入口（1, 1）标记为已访问maze[1][1] = 1;// 调用 dfs 函数开始搜索dfs(1, 1, 0);// 输出最终找到的最短路径cout << ans << endl;// 输出最短路径的步数cout << best << endl;return 0;
}

这段代码的主要逻辑是通过深度优先搜索来遍历迷宫的所有可能路径，同时记录并更新最短路径。在搜索过程中，使用了一个二维数组 mins 来记录从起点到每个点的最短步数，以及一个字符数组 a 来记录路径中的每一步移动方向。当到达终点时，会检查当前路径的步数是否比已知的最短路径更短，或者在步数相同的情况下是否字典序更小。如果满足条件，就会更新最短路径。最后，程序输出找到的最短路径及其步数。

难点解释：pos+1<=mins[tox][toy]

在这段代码中，pos+1<=mins[tox][toy] 这一行的作用是检查当前扩展的路径是否可能成为到达新位置 (tox, toy) 的更短或等长但字典序更优的路径。

具体来说，这里的 pos 表示当前路径的步数，mins[tox][toy] 存储的是到达位置 (tox, toy) 的最短步数。如果 pos+1（即当前路径步数加一，因为我们要移动到新位置）小于或等于 mins[tox][toy]，这意味着我们找到了一个到达该位置的路径，其步数不比已知的最短步数多，或者步数相同时路径的字典序更优（因为在这段代码中，路径是通过字符数组 a 记录的，所以可以直接比较字符串的字典序）。

如果 pos+1 大于 mins[tox][toy]，那么当前路径不会是到达 (tox, toy) 的最短路径，因此没有必要继续在这个方向上搜索，可以剪枝，节省搜索时间。

这个条件检查是典型的在图搜索算法中用于优化和剪枝的技巧，它帮助算法避免在不可能改善当前最短路径的方向上浪费时间。通过这种方式，算法可以保证在找到出口时，记录的路径是最短的，并且在步数相同时字典序最小的路径。

踩过的坑：memset(mins, 1, sizeof(mins));

这里我没理解memset函数的作用，其实memset这个函数只能将整型数组初始化为0和-1，对于其他数字的初始化则不行，例如这里memset(mins, 1, sizeof(mins));则是将mins数组初始化为16843009，这是一个非常大的数

BFS

#include<bits/stdc++.h> // 包含所有标准库
using namespace std;
typedef pair<int,int> PII; // 定义一个类型别名，方便表示坐标对const int col=30,row=50; // 定义迷宫的列数和行数// 迷宫的布局，0表示可通行的路径，1表示障碍
int mp[col][row] = {
0,1,0,1,0,1,0,1,0,0,1,0,1,1,0,0,1,0,0,1,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,1,0,1,0,
0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,0,0,1,1,0,0,1,1,0,1,0,0,1,0,1,
0,1,1,1,1,0,1,1,0,1,0,0,1,0,0,0,1,0,0,0,0,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,1,1,0,0,0,0,0,0,0,1,0,0,0,0,
0,1,0,0,0,0,0,0,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,1,0,0,1,0,1,1,
0,0,0,1,1,1,1,1,0,0,0,0,0,0,1,0,1,0,0,0,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,1,0,1,1,0,0,0,0,0,0,0,0,
1,1,0,0,1,0,0,0,1,1,0,1,0,1,0,0,0,0,1,0,1,0,1,1,0,0,0,1,1,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,0,1,1,1,
0,0,0,1,1,0,1,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,1,0,0,0,0,0,0,0,
1,0,1,0,0,0,0,0,1,0,1,0,0,0,1,0,0,1,1,0,1,0,1,0,1,0,1,1,1,1,1,0,0,1,1,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0,
0,0,1,1,1,0,0,0,0,0,1,0,1,0,1,0,0,0,0,1,1,0,0,0,1,0,0,0,0,0,0,1,0,0,0,1,0,1,0,0,1,1,0,0,0,0,1,0,0,1,
1,1,0,0,0,1,1,0,1,0,0,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,0,0,1,1,0,1,0,0,0,
0,0,0,1,0,0,0,0,1,0,0,1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,1,0,1,0,0,0,1,0,1,0,1,0,1,0,0,0,0,1,0,1,
1,1,1,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,1,0,1,0,1,0,1,0,1,0,0,1,0,0,1,0,0,0,1,0,1,0,0,
0,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,1,1,0,0,1,1,1,1,0,1,0,0,0,1,1,0,0,0,0,0,1,0,1,0,1,0,1,0,0,0,1,1,
1,0,1,0,1,0,1,0,0,1,1,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,1,0,1,1,0,0,1,1,1,1,0,1,1,0,1,0,0,0,0,1,0,0,0,
1,0,1,0,1,0,1,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,1,1,1,0,1,1,1,0,1,0,0,1,
1,0,0,0,0,0,0,0,1,0,1,1,0,0,0,1,0,0,0,0,1,0,1,1,0,0,1,0,1,1,0,1,0,0,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,
1,0,1,0,1,0,0,1,0,0,0,0,0,0,0,1,0,1,0,0,1,0,0,0,0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,1,1,1,1,0,1,0,1,0,0,1,
0,0,1,0,1,0,0,1,0,1,0,1,0,1,1,0,1,0,0,1,0,1,0,1,0,0,0,1,1,0,1,0,1,0,1,1,0,1,1,1,0,0,0,0,1,1,0,1,0,1,
1,1,0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,0,0,0,1,0,0,0,1,1,1,0,0,0,0,1,0,
0,0,0,0,1,0,0,0,1,1,0,0,0,0,1,1,0,1,0,1,1,0,1,0,0,0,0,0,0,1,0,0,1,0,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,
1,0,1,0,0,1,0,1,0,0,0,1,0,1,0,0,0,0,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,1,0,1,0,1,1,0,1,0,1,0,1,0,0,0,0,1,
0,0,1,0,1,0,0,0,0,1,0,0,0,0,1,1,0,1,0,1,0,1,0,0,0,0,1,0,0,0,1,0,0,0,1,0,0,1,0,0,0,1,0,0,0,1,0,1,0,1,
1,0,1,0,0,0,0,1,0,0,0,1,1,0,0,1,0,0,0,1,0,0,0,0,1,0,1,0,1,0,0,1,0,1,0,1,0,1,0,1,1,1,1,1,0,1,0,0,1,0,
0,0,0,0,0,1,0,0,1,0,1,0,0,0,0,0,0,1,1,0,0,1,0,1,0,0,1,0,1,0,0,1,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,1,0,
1,1,0,1,0,0,0,0,0,0,1,0,0,1,1,1,0,1,1,1,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,0,1,1,0,1,1,1,0,1,0,0,0,
0,0,0,0,0,1,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,0,0,0,0,1,0,0,0,0,1,1,1,0,1,0,0,0,0,0,0,1,1,0,0,1,1,
1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,1,0,0,0,1,1,1,1,1,0,0,0,1,0,1,0,1,0,0,1,0,1,0,0,0,0,0,0,1,0,0,0,
1,0,0,0,0,0,1,0,1,0,0,1,0,1,0,0,1,0,1,0,1,1,0,0,0,0,0,0,0,1,0,0,1,0,1,0,1,0,0,0,1,0,1,1,1,0,1,0,0,0,
0,0,1,1,1,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,1,1,0,1,1,1,0,0,0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,1,0,1,1,
1,0,0,0,0,0,0,1,1,0,0,1,1,1,0,1,0,1,1,1,0,1,0,0,0,1,0,0,0,1,1,0,1,1,1,0,1,0,1,0,1,1,0,1,1,1,1,0,0,0
};int d[col+1][row+1]; // 定义一个二维数组，用于记录从起点到每个点的最短距离queue<PII> p; // 创建一个队列，用于存放待探索的坐标// 定义一个结构体，用于记录路径信息
struct node {int x; // 父节点的x坐标int y; // 父节点的y坐标char s; // 父节点的方向
};node fa[col][row]; // 创建一个二维数组，用于记录每个点的父节点信息// dx和dy数组用于表示四个方向的相对坐标变化
int dx[5] = {1, 0, 0, -1};
int dy[5] = {0, -1, 1, 0};// dir数组用于表示四个方向的字符，按照字典序排序
char dir[5] = {'D', 'L', 'R', 'U'};// 判断函数，用于检查坐标是否在迷宫内，且为可通行的路径，且未被探索过
int judge(int x, int y) {if (x >= 0 && x < col && y >= 0 && y < row && mp[x][y] == 0 && d[x][y] == -1)return 1;return 0;
}// 深度优先搜索函数，用于探索迷宫
void dfs(int x, int y) {if (x == col - 1 && y == row - 1) // 如果到达终点，则停止搜索return;elsedfs(fa[x][y].x, fa[x][y].y); // 递归探索父节点//因为father(29,49)存储了它上一个位置在哪，那么就可以顺藤摸瓜的找出再上一个位置//如此搜索下去，直到搜到（0，0）位置而终止，返回上一层打印出所记录的direction方位，//逐层返回，就把从（0，0）走到（29，49）所途径的所有点时的direction都打印出来了cout << fa[x][y].s; // 输出路径
}int main() {memset(d, -1, sizeof(d)); // 初始化距离数组，将所有值设为-1，表示未探索p.push({0, 0}); // 将起点加入队列d[0][0] = 0; // 起点到起点的距离设为0while (p.size() != 0) { // 当队列不为空时，循环探索PII t = p.front(); // 取出队列中的第一个元素p.pop();for (int i = 0; i < 4; i++) { // 遍历四个方向int tx = t.first + dx[i]; // 计算目标坐标int ty = t.second + dy[i];if (judge(tx, ty)) { // 如果目标坐标可通行d[tx][ty] = d[t.first][t.second] + 1; // 更新距离p.push({tx, ty}); // 将目标坐标加入队列fa[tx][ty].x = t.first; // 记录父节点坐标fa[tx][ty].y = t.second;fa[tx][ty].s = dir[i]; // 记录方向//father(tox,toy)的x、y、s表明了//走到（tox，toy）这个点，是从其（x，y）点往s方向而来的 //换句话说，就是存储了它的上一个点的位置，以及从何方位而来 }}}dfs(col - 1, row - 1); // 从终点开始回溯，输出路径return 0;
}

这段代码的主要功能是找到从迷宫的左上角（起点）到右下角（终点）的最短路径，并按照字典序输出路径。代码使用了深度优先搜索算法，通过一个队列来实现层级遍历，同时记录每个点的父节点信息，以便最后回溯输出路径。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/287173.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【数据结构】双向奔赴的爱恋 --- 双向链表

【数据结构】双向奔赴的爱恋 --- 双向链表

关注小庄 顿顿解馋๑ᵒᯅᵒ๑ 引言&#xff1a;上回我们讲解了单链表(单向不循环不带头链表)&#xff0c;我们可以发现他是存在一定缺陷的&#xff0c;比如尾删的时候需要遍历一遍链表&#xff0c;这会大大降低我们的性能&#xff0c;再比如对于链表中的一个结点我们是无法直接…
阅读更多...
思通舆情 是一款开源免费的舆情系统 介绍

思通舆情 是一款开源免费的舆情系统 介绍

思通舆情 是一款开源免费的舆情系统。 支持本地化部署&#xff0c;支持在线体验。 支持对海量舆情数据分析和挖掘。 无论你是使用者还是共同完善的开发者&#xff0c;欢迎 pull request 或者 留言对我们提出建议。 您的支持和参与就是我们坚持开源的动力&#xff01;请 sta…
阅读更多...
超越Sora！StreamingT2V AI视频模型，轻松打造120秒视觉盛宴

超越Sora！StreamingT2V AI视频模型，轻松打造120秒视觉盛宴

近日&#xff0c;来自美国德克萨斯大学奥斯汀分校&#xff08;UT奥斯丁&#xff09;等机构的研究人员提出了一项名为StreamingT2V的AI视频生成技术&#xff0c;引起了业界的广泛关注。这项技术打破了传统视频生成的局限&#xff0c;实现了高度一致且长度可扩展的视频生成&#…
阅读更多...
C语言（结构体，联合体，枚举的讲解）

C语言（结构体，联合体，枚举的讲解）

这期我们来讲解结构体&#xff0c;联合体&#xff0c;以及枚举的讲解&#xff0c;首先我们从概念开始一步一步的了解。 1&#xff0c;结构体 1.1概念 C 语言中的结构体是一种用户自定义的数据类型&#xff0c;它允许你将不同类型的变量组合在一起&#xff0c;从而形成一个新…
阅读更多...
1978-2022年全国31省社会消费品零售总额数据

1978-2022年全国31省社会消费品零售总额数据

1978-2022年全国31省社会消费品零售总额数据 1、时间&#xff1a;1978-2022年 2、指标&#xff1a;社会消费品零售总额 3、范围&#xff1a;31省市 4、来源&#xff1a;整理自国家统计J和各省年鉴 5、缺失情况说明&#xff1a;1997-2022年31省市均无缺失&#xff0c; 199…
阅读更多...
海外媒体发稿：9种高效的媒体套餐内容发稿策略分析-华媒舍

海外媒体发稿：9种高效的媒体套餐内容发稿策略分析-华媒舍

海外媒体发稿&#xff1a;9种高效的媒体套餐内容发稿策略分析高效的媒体发布和营销推广策略对公司、本人的成就尤为重要。下面我们就对于媒体套餐内容发稿营销推广策略开展全面解析&#xff0c;帮助读者掌握并应用这9种合理的思路&#xff0c;进而获得更好的媒体营销效果。 1.媒…
阅读更多...
【Python系列】Python 中 YAML 文件与字典合并的实用技巧

【Python系列】Python 中 YAML 文件与字典合并的实用技巧

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
阅读更多...
Focal Modulation Networks聚焦调制网络

Focal Modulation Networks聚焦调制网络

摘要 我们提出了 焦点调制网络 &#xff08;简称 FocalNets) &#xff0c;其中 自注意&#xff08; SA &#xff09;被 Focal Modulation 替换&#xff0c;这种机制 包括三个组件&#xff1a;&#xff08; 1 &#xff09;通过 depth-wise Conv 提取分级的上下文信息&#xff0…
阅读更多...
数据丢失大拯救：格式化后如何高效恢复文件

数据丢失大拯救：格式化后如何高效恢复文件

一、遭遇格式化危机&#xff0c;数据恢复有妙招 在数字化时代&#xff0c;数据丢失无疑是让人头疼的问题之一。特别是当存储设备意外格式化后&#xff0c;许多用户都会感到手足无措&#xff0c;不知如何是好。那么&#xff0c;格式化了怎么恢复呢&#xff1f;其实&#xff0c;…
阅读更多...
黑马头条day5总结

黑马头条day5总结

1、surefire-reports for the individual test results. 借鉴&#xff1a;【已解决】surefire-reports for the individual test results.-CSDN博客 Please refer to D:\javashizhan01\heima-leadnews\heima-leadnews-service\heima-leadnews-article\target\surefire-report…
阅读更多...
【@changesets/cli】变更集实战教程

【@changesets/cli】变更集实战教程

一、背景概述 前端目前基于Monorepo架构的npm包开发很普遍&#xff0c;在开发完毕后&#xff0c;我们需要对包进行版本号升级&#xff0c;并且部署&#xff0c;这些操作如果是手动来操作的话&#xff0c;很麻烦&#xff0c;而且容易出错。 例如有这样的场景&#xff1a; -ap…
阅读更多...
【Java程序设计】【C00345】基于Springboot的船舶监造管理系统（有论文）

【Java程序设计】【C00345】基于Springboot的船舶监造管理系统（有论文）

基于Springboot的船舶监造管理系统&#xff08;有论文&#xff09; 项目简介项目获取开发环境项目技术运行截图 项目简介 项目获取 &#x1f345;文末点击卡片获取源码&#x1f345; 开发环境 运行环境&#xff1a;推荐jdk1.8&#xff1b; 开发工具&#xff1a;eclipse以及i…
阅读更多...
敏捷开发最佳实践：学习与改进维度实践案例之会诊式培养敏捷教练

敏捷开发最佳实践：学习与改进维度实践案例之会诊式培养敏捷教练

自组织团队能够定期反思并采取针对性行动来提升人效&#xff0c;但2022年的敏捷调研发现&#xff0c;70%的中国企业在学习和改进方面仍停留在团队级。本节实践案例将分享“会诊式培养敏捷教练”的具体做法&#xff0c;突出了敏捷以人为本的学习和改进&#xff0c;强调了通过人员…
阅读更多...
Java前缀和

Java前缀和

一维前缀和&#xff1a; public class Main {private static final int N 100010;public static void main(String[] args) {int[] s new int[N];int[] a new int[N];int n 10;// 定义10个数for (int i 1; i < n; i) {a[i] (int) (Math.random() * 10);}for (int i 1…
阅读更多...
大模型时代的向量数据库：原理解析和应用案例

大模型时代的向量数据库：原理解析和应用案例

大家好&#xff0c;在人工智能领域&#xff0c;数据处理和加工的需求愈发增加。随着人们深入探索AI高级的应用&#xff0c;如图像识别、语音搜索和推荐引擎等&#xff0c;数据的复杂性也在不断地增加。此时传统的数据库存储方式已不能完全满足需求&#xff0c;向量数据库应运而…
阅读更多...
Java零基础入门到精通_Day 2

Java零基础入门到精通_Day 2

18 算数运算符 - * / % 整数的运算只能得到整数 除非用浮点数进行运算&#xff08;得到浮点数&#xff09; public class Base_002 {public static void main(String[] args) {double a 6.0;int b 4;System.out.println(a/b); //1.5} } 19 字符的操作 public class Base_0…
阅读更多...
大模型面试准备（五）：图解 Transformer 最关键模块 MHA

大模型面试准备（五）：图解 Transformer 最关键模块 MHA

节前&#xff0c;我们组织了一场算法岗技术&面试讨论会&#xff0c;邀请了一些互联网大厂朋友、参加社招和校招面试的同学&#xff0c;针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何备战、面试常考点分享等热门话题进行了深入的讨论。 合集在这…
阅读更多...
【Godot4自学手册】第二十九节使用Shader来实现敌人受伤的闪白效果

【Godot4自学手册】第二十九节使用Shader来实现敌人受伤的闪白效果

在Godot 4中&#xff0c;Shader是用来为材质提供自定义渲染效果的程序。材质可以应用于MeshInstance、CanvasItem和ParticleEmitter等节点。Shader可以影响顶点的变换、片段&#xff08;像素&#xff09;的颜色&#xff0c;以及光照与物体的交互。 在Godot中&#xff0c;Shader…
阅读更多...
C#_事件_多线程(基础)

C#_事件_多线程(基础)

文章目录 事件通过事件使用委托 多线程(基础)进程:线程: 多线程线程生命周期主线程Thread 类中的属性和方法创建线程管理线程销毁线程 昨天习题答案 事件 事件&#xff08;Event&#xff09;本质上来讲是一种特殊的多播委托&#xff0c;只能从声明它的类中进行调用,基本上说是…
阅读更多...
【小沐学AI】智谱AI大模型的一点点学习（Python）

【小沐学AI】智谱AI大模型的一点点学习（Python）

文章目录 1、简介1.1 大模型排行榜 2、智谱AI2.1 GLM2.1.1 模型简介2.1.2 开源代码2.1.2.1 GLM-130B 2.2 ChatGLM2.2.1 模型简介2.2.2 开源代码2.2.2.1 ChatGLM2.2.2.2 ChatGLM22.2.2.3 ChatGLM3 2.3 CodeGeeX2.3.1 模型简介2.3.2 开源代码 2.4 CogView2.4.1 模型简介2.4.2 开源…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023