javaScript——BFS结合队列求迷宫最短路径

这里推荐先去看下B站这个老师讲的BFS迷宫问题，只用看前五分钟就能懂用BFS+队列实现的原理。[POJ] 3984 迷宫问题 BFS_哔哩哔哩_bilibili

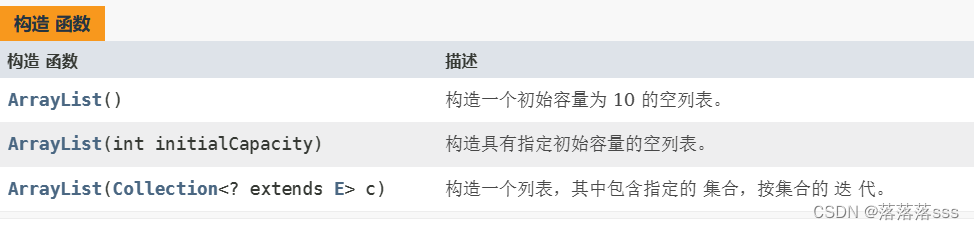
问题描述：由m*n的矩阵构成了一个迷宫，矩阵中为1的元素表示障碍物，不能走，为0表示可以走。同时，可以你可以竖着或横着走都行，也就是四个方向都可以。问：从起点到终点的最短路径是多少，并输出最短路径上的路径信息。

思路：采用广度优先搜索的方式，尝试让某个点朝四个方向各走一步，如果都能走通，将这些路径和步长入队。每次都对队列的元素尝试往前走一步，最早找到终点的路径就是要求的最短路径。我们定义的方向是下、上、右、左。假设由两个点分别向下、向右走一步都到了终点，并且两者的step相等，那么，先遍历的也就是向下的这个路径作为目标输出。即使路径长度都一样，只要一个即可。

广度遍历不需要回溯：开始时用队列存储第一个为遍历的节点。从第一个点开始，将它shift出去，然后尝试向四周走一步，如果走的通，将那个节点和路径信息入队，依次遍历所有方向。

下次遍历时，队列里是步长为1的准备往下一步的节点了。跟之前一样，挨个shift出去，然后你就尝试四周走吧。。。直到已遍历到end节点结束。

大白话思想：从根节点出发，每次只走一步（四个方向都考虑一下），或者阻塞了走不了；走不了也shift出去了，下次不带他继续走了。每次都带着可以走的节点继续往前走。最先走到终点的节点就是循环结束。如果找不到，返回-1。

function shortestPath(maze, start, end) {const rows = maze.length;const cols = maze[0].length;//定义方向const directions = [[0, 1], //向下走一步，[0, -1], //向上走一步[1, 0], //向右走一步[-1, 0], //向左走一步];const visited = Array.from(Array(rows), () => Array(cols).fill(false));const queue = [[start, 0, []]];while (queue.length > 0) {const [[X, Y], steps, path] = queue.shift();if (X === end[0] && Y === end[1]) {return [steps, path.concat([[X, Y]])];}for (let dir of directions) {const [dx, dy] = dir;const newX = X + dx;const newY = Y + dy;if (newX >= 0 &&newX < rows &&newY >= 0 &&newY < cols &&maze[newX][newY] == 0 &&!visited[newX][newY]) {visited[newX][newY] = true;queue.push([[newX, newY], steps + 1, path.concat([[X, Y]])]);}}}return [-1, []];
}
// 示例迷宫
const maze = [[0, 1, 0, 0, 0],[0, 0, 0, 1, 0],[1, 1, 0, 1, 0],[1, 1, 0, 0, 0],[0, 0, 0, 0, 0],
];const start = [0, 0]; // 起点坐标
const end = [4, 4]; // 终点坐标const [steps, path] = shortestPath(maze, start, end); // 调用函数计算最短路径
if (steps !== -1) {console.log(`最短步数为：${steps}`); // 输出最短步数console.log("最短路径为：" + "[" + path.join("]->[") + "]"); // 输出最短路径
} else {console.log("未找到路径"); // 输出未找到路径的提示
}