every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog
0. 前言
统计学基础
1. 频率派
频率学派(传统学派)认为样本信息来自总体,通过对样本信息的研究可以合理地推断和估计总体信息,并且随着样本的增加,推断结果会更加准确。代表性人物是费希尔(R. A. Fisher, 1890-1962)。

频率学派的核心思想是基于大样本理论,将概率看作频率的极限,以样本观测值的频率为基础进行推断。频率学派注重数据的重复抽样和统计量的性质,比如点估计、置信区间和假设检验等。它强调的是通过样本信息来推断总体参数,并将此过程视为客观的、可重复的。
2. 贝叶斯学派
贝叶斯学派源于英国学者贝叶斯(T. Bayes, 1702-1761)在1763年发表的著名论文《论有关机遇问题的求解》。贝叶斯学派认为任何一个未知量都可以看作是随机的,应该用一个概率分布去描述未知参数,而不是频率派认为的固定值。

贝叶斯学派的核心思想是先验信息与后验信息相结合,通过贝叶斯公式将先验信息与样本数据进行结合,得到后验分布,并以此作为对未知参数的推断。贝叶斯学派强调主观先验信息的引入,因此不同人可能会有不同的先验分布,从而导致不同的推断结果。贝叶斯学派注重个体的主观判断和背景信息,更加灵活和主观。

先验分布: 贝叶斯学派使用先验分布来描述对未知参数的主观先验知识。先验分布可以是任意形式的分布函数,它反映了我们在进行观测之前对参数的先验认识。例如,在研究某产品的平均寿命时,我们可以使用指数分布作为平均寿命的先验分布。
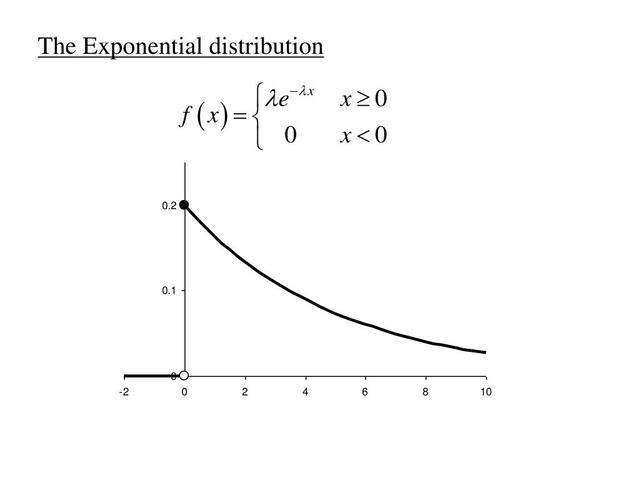
后验分布: 贝叶斯学派使用后验分布来描述在观测数据之后对未知参数的更新认识。后验分布是通过将先验分布与观测数据相结合,应用贝叶斯公式计算得到的。例如,在进行文本分类时,我们可以使用贝叶斯定理计算每个类别的后验概率,从而将文本归入最可能的类别中。

3. 案例
3.1 频率派
比如我们想了解一个公交站在下一个单位时间内候车的人数情况。
常识告诉我们候车的人数分布应该是符合泊松分布的:
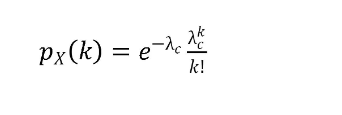
也就是说单位时间内有k个人候车的概率,我们可以通过带入这个公式直接计算出来。
但是,我们面对的问题就是我们虽然知道这个分布公式,但其中有个未知参数λc。
所以,我们需要做的就是在已知分布的情况下如何去估计分布中未知的参数λc。
参数估计的经典方法认为未知参数λc是一个固定的常数,只不过是我们并没有确切的知道这个值。但是我们可以通过抽样得到的数据信息对这个值进行估计。
为此费希尔把高斯的极大似然估计方法做了重新论述,使之用来对参数进行估计。
简要说一下这个方法的大概思路。
我们从车站观察了5次,x1、x2、x3、x4、x5,我们认为在仅有的实验条件下出现的结果应该就是最大概率出现的结果。
所以我们写出似然函数:
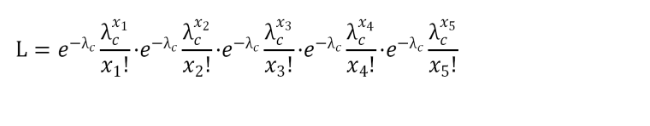
然后求使得这个式子达到最大值的λc的值。
由于对数的单调性,通常会取对数再求极值。
具体计算省略掉,得到的值为:
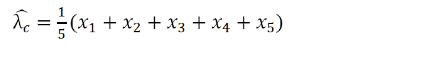
这便是费希尔的经典方法。
3.2 贝叶斯派
贝叶斯学派的最基本观点就是:任何一个未知量都可以看作是随机的,应该用一个概率分布去描述未知参数,而不是频率派认为的固定值。
在进行参数估计之前,通过先验信息,我们常常可以得到一个关于未知参数的概率分布,即先验分布,或主观分布。
这在频率派看来是根本不允许的,说好的未知参数是一个固定值,只能通过大量的重复的实验频率来确定,怎么到这里成了一个不确定的值了呢?
一句话而言,频率派认为未知参数是客观的,贝叶斯派认为未知参数可以先从主观角度来考虑。
贝叶斯认为,λc 不应该是一个固定值,而应该是一个随机变量。
我们平时根据经验,可以对做出一个分布的估计。
在这个例子中,我们根据平时候车的经验,感觉λc的值有75%的可能是10,有25%的可能是8,基本上没有其他的可能性了。
用贝叶斯方法的描述就是,关于λc的先验分布为:

如果我们现在去公交车站,观察了一次,X=7,也就是说我们获得了最新的数据信息。
最新的数据信息有助于我们更新对λc的认识,即更新关于λc的先验分布。
应用贝叶斯定理,得到:



同理得,
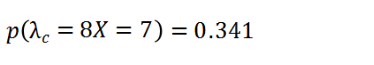
所以,通过我们获得的信息,我们更新了我们对于先验分布的认识,从而得到了后验分布。
从认知的角度而言,贝叶斯方法是一个动态的过程。
随着我们经验的积累、获取数据的积累,对未知参数的估计不断进行着调整。
所以,贝叶斯方法很快在自然语言处理方面展现出了较好的特性。
4. 小结
频率学派和贝叶斯学派在理论和实践中各有侧重,互为补充。
频率学派的优点是注重大样本下的一致性和渐进性质,在样本足够大的情况下可以得到较为准确的推断结果。它的方法论在经典统计推断中应用广泛,特别适用于重复试验或大规模数据的分析。
贝叶斯学派的优点是能够充分利用先验信息,并将其与样本数据结合,从而得到更准确的推断结果。它的方法论适用于小样本或无法进行重复试验的情境,以及需要考虑个体差异和主观判断的问题。
参考
- https://mp.weixin.qq.com/s?__biz=MjM5MDE3OTk2Ng==&mid=2657441571&idx=1&sn=8448415b9c3fa355e76918f88dcb9f7b&chksm=bdd940328aaec9249e769779007899e55bd7d2fb7fa4cb2c785896cabb61fd9d36a93a93c6be&scene=27
- https://blog.csdn.net/fmqdzh/article/details/120003189
- https://blog.csdn.net/zy_zhengyang/article/details/115529564
- https://baijiahao.baidu.com/s?id=1779292867410400878&wfr=spider&for=pc