Day 58

01. 判断子序列（No. 392）

题目链接

代码随想录题解

<1> 题目

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

致谢：特别感谢 @pbrother 添加此问题并且创建所有测试用例。

示例 1：

输入：s = “abc”, t = “ahbgdc”
输出：true

示例 2：

输入：s = “axc”, t = “ahbgdc”
输出：false

提示：

• 0 <= s.length <= 100
• 0 <= t.length <= 10^4
• 两个字符串都只由小写字符组成。

<2> 题解

如果仅考虑动态规划解法的话，本题是昨天的 最长公共子序列 的简化版本。

子序列的定义为：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

**s 是否是 t 的公共子序列，其实也就代表了 t 和 s 的最长公共子序列是否是 s。**所以本题的动态规划解法就是求得它们两个最长公共子序列的长度，然后判断长度是否等于 s 的长度即可；剩下的步骤和求最长公共子序列的方法就完全相同了。

1. 状态

既然是求最长的公共子序列，那就涉及到 长度，可以分解成如下的子问题：

s 的前一个元素和 t 第一个元素组成的最长公共子序列是多少？

s 的前两个元素和 t 第一个元素组成的最长公共子序列是多少？

s 的前三个元素和 t 第一个元素组成的最长公共子序列是多少？

。。。。。。

一直推到到 s 的前 s.length() 个元素和 t 的前 t.length() 个元素的最长公共子序列的长度为多少。

那这个状态能否转移呢？s 的前 m 个元素和 t 的前 n 个元素的公共子序列的长度，是可以通过 m - 1 和 n - 1 组成的公共子序列的长度推出的。

2. dp 数组的含义

dp 数组设定为一个二维数组 dp[i][j] 表示 s 的钱 i - 1 个元素和 t 的前 j - 1 个元素构成的最长公共子序列的大小。

使用这种后移一位的方式可以减少初始化的复杂程度。

3. 递推公式

对于 s 的第 i 个元素和 t 的第 j 个元素有两种情况：

• 它们是相等的，所以它们可以作为构成子序列的元素存在
• 它们不相等，在这个 长度范围 内需要被剔除

如果它们相等，那

dp[i][j] = dp[i - 1][j - 1] + 1

如果它们不相等，那就是延续前面的子序列在如下三个中取最大：

• dp[i - 1][j]
• dp[i - 1][j - 1]
• dp[i][j - 1]

但因为第二种情况被包含了，所以仅对前两个情况取值即可，也就是

dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);

4. 初始化

本题中，下层的推导依赖的是左上角的值，所以只需要初始化第一行和第一列即可。

而本题的第一行代表 s 的第 0 个元素（从 1 开始，0 没有意义）和 t 的最长公共子序列，为 0

第一列代表着 t 的第 0 个元素和 s 的最长公共子序列，也是 0

所以均初始化为 0 即可，也就是不需要初始化。

<3> 代码

class Solution {public boolean isSubsequence(String s, String t) {int m = 0;int n = 0;while (m < s.length() && n < t.length()) {if (s.charAt(m) == t.charAt(n)) {m++;n++;} else {n++;}}return m == s.length();}
}

02. 不同的子序列（No. 115）

题目链接

代码随想录题解

<1> 题目

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数，结果需要对 10⁹ + 7 取模。

示例 1：

输入：s = “rabbbit”, t = “rabbit”
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = “babgbag”, t = “bag”
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag

提示：

• 1 <= s.length, t.length <= 1000
• s 和 t 由英文字母组成

<2> 题解

1. 状态

本题虽然是困难题，但只要选好转移的状态，解答起来就比较简单了。

本题是要查询 s 中有多少种方法可以得到 t，比如第一个案例 s = “rabbbit”, t = “rabbit”，首先来考虑如何划分这个子问题：既然我去查询 s 有多少种方法可以得到 “rabbit” 比较困难，那能否先去找方法得到 “t” 呢？在之后能否得到 “it” 呢？

好，现在其实子问题的拆分就很明确了

• s 中得到 “t” 有多少种方法？

• s 中得到 “it” 有多少种方法？

• s 中得到 “bit” 有多少种方法？

• s 中得到 “bbit” 有多少种方法？

  。。。。。。

• s 中得到 “rabbit” 有多少种方法？

这种考虑方式是从后往前去考虑的，其实也可以从前往后去转移。

那这个状态能否转移呢？

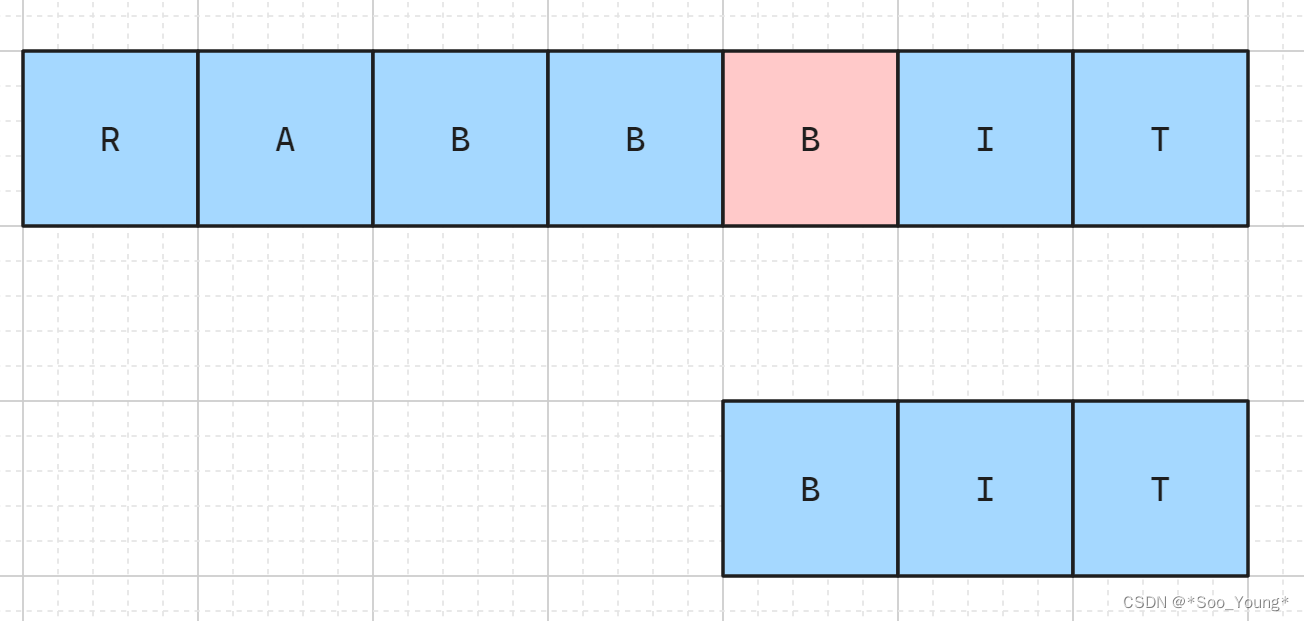
比如说现在要组成 BIT 这个序列，现在遍历到粉色的 B 了，现在，只需要知道，它后面的部分 能有几种方法组成 IT 就可以了。

2. dp 数组

本题需要一个二维的 dp 数组：

s = "rabbbit", t = "rabbit"

以上面的测试案例举例，dp[i][j] 表示目标字符串 t 从 i 到 末尾的字段在源字符串 s 从 j 到末尾的范围内有多少种构成的方式。

比如说 dp[3][0] 就是从 0 到 s.length - 1 这个范围内（“rabbbit”）构成 从 3 到 t.length - 1（“bit”）有几种方式。

3. 递推公式

还是举一个例子比较好理解：

比如说现在要计算这个节点，有多少种构成 BIT 的方式，就是要在这里寻找为 B 的节点

这时候它的前一层，也就是 dp[i + 1][j + 1] 表示从这个节点的后面开始，构成 IT 这个字段的方法

那这个节点构成 BIT 的方法就是 dp[i + 1][j + 1] 种嘛？是不对的，还需要再加上后一个节点构成 BIT 的方法，因为此时得到 BIT 的方法有如下两种：

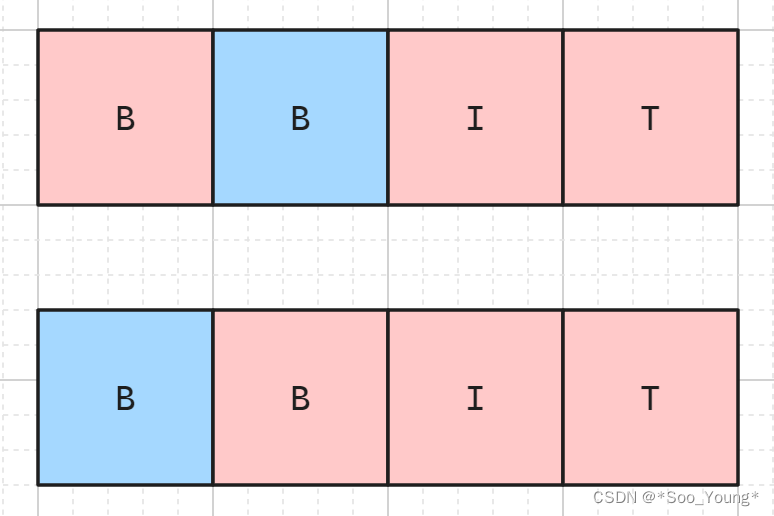
所以最终得到的递推公式就是这样：

dp[i][j] = dp[i + 1][j + 1] + dp[i][j + 1];

搞清楚递推公式的含义非常关键。

那对于不相等的情况：

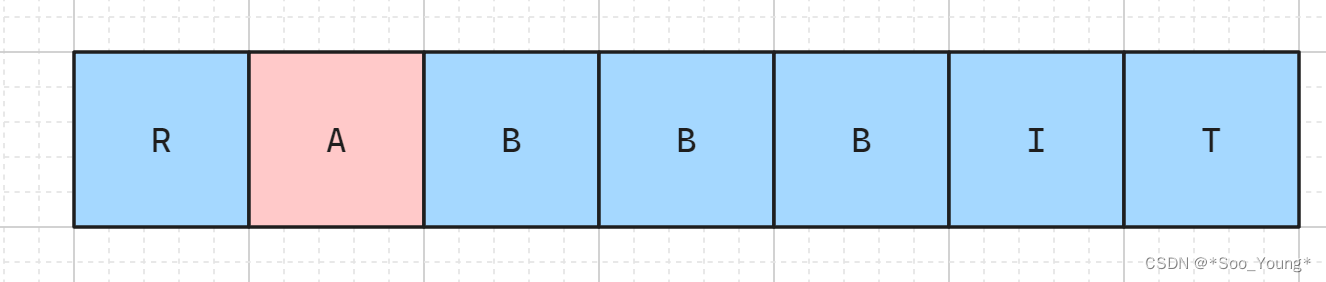
比如这里的节点 A，那此时从 A 到末尾构成 BIT 的方法就是它后面那个节点构成 BIT 的方法，得到：

dp[i][j] = dp[i][j + 1];

4. 初始化

因为本题的所有推导都是依赖第一行的，所以要先对第一行进行初始化

if (c1[c1.length - 1] == c2[c2.length - 1]) dp[c1.length - 1][c2.length - 1] = 1;for (int i = c2.length - 2; i >= 0; i--) {if (c2[i] == c1[c1.length - 1]) dp[c1.length - 1][i] = dp[c1.length - 1][i + 1] + 1;else dp[c1.length - 1][i] = dp[c1.length - 1][i + 1];}

先对最后一个元素进行特殊的处理，其他逻辑和前面的相同

<3> 代码

class Solution {public int numDistinct(String s, String t) {if (s.length() <= t.length()) {return s.equals(t) ? 1 : 0;}char[] c1 = t.toCharArray(); // 目标序列char[] c2 = s.toCharArray(); // 提供的序列int[][] dp = new int[c1.length][c2.length];if (c1[c1.length - 1] == c2[c2.length - 1]) dp[c1.length - 1][c2.length - 1] = 1;for (int i = c2.length - 2; i >= 0; i--) {if (c2[i] == c1[c1.length - 1]) dp[c1.length - 1][i] = dp[c1.length - 1][i + 1] + 1;else dp[c1.length - 1][i] = dp[c1.length - 1][i + 1];}for (int i = c1.length - 2; i >= 0; i--) {// 外层遍历要寻找的数组 c2for (int j = c2.length - 2; j >= 0; j--) {if (c1[i] == c2[j]) {dp[i][j] = dp[i + 1][j + 1] + dp[i][j + 1];} else {dp[i][j] = dp[i][j + 1];}}}return dp[0][0];}
}