104. 货仓选址 - AcWing题库

有n家商店，求把货仓建在哪能使得货仓到每个点的距离总和最小，输出最短的距离总和。

首先，我们看只有两个点的情况，在这种情况下我们选[1,2]的任何一个位置都是一样的，总和就是这段区间的长度，对吧。

如果扩展到n个点呢？我们两两配对来看。

首先只看1，n这个区间，那么这个点选在[1,n]都是等价的对吧，而且是最优的。因此，我们缩小范围到[1,n]。

再来看看2，6这段呢，选在[2,6]是不是也是答案最优的？因此我们进一步缩小范围。

3,5这段，进一步缩小范围到[3,5]。

此时只剩下一个点4了，选在点上肯定比不在点上要好。因此我们的答案就是4了。

如果正好是偶数个呢？那我们是不是选在最中间区间内的任一一点就好了，因为最后答案就是这几段小区间的长度之和。

具体到代码上呢，奇数就选最中间那个点，n/2+1。偶数，n/2或者n/2+1都可。我们直接一般化输出n/2+1。也就是数组的中位数。

#include<bits/stdc++.h>
using ll=long long;
const int N=2e5+10;
int n,m,k;
int a[N];
ll ans;
void solve()
{std::cin>>n;for(int i=1;i<=n;i++){std::cin>>a[i];	}	std::sort(a+1,1+a+n);for(int i=1;i<=n;i++){ans+=std::abs(a[i]-a[n/2+1]);} std::cout<<ans;
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}

我们推广到一般情况：

P1031 [NOIP2002 提高组] 均分纸牌 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

首先来看线性均分纸牌问题。

为什么可以这样写？

这段代码成立的基础就在于只能移给相邻的堆。那么，1只能跟2交换以达到target，1换好之后2就只能跟3交换（因为如果1跟2又换了1就不是target了，而且说明前面做了无用功，答案一定不是最优的）。因此可以这样一条线递推。

（感觉这个递推思想有点类似于费解的开关，每个灯能改变上下左右相邻的状态，第一行的灯只能由第二行改变，一旦第一行灯的状态确定了，则第二行、第三行......第n行的状态也就确定了。所以那题就枚举第一行的状态就行）。

#include<bits/stdc++.h>
using ll=long long;
const int N=2e5+10;
const int mod=1e9+7;
int a[N];
int n;
ll s=0,cnt;
void solve()
{std::cin>>n;for(int i=1;i<=n;i++){std::cin>>a[i];s+=a[i];}s/=n;for(int i=1;i<=n;i++){if(a[i]<s) a[i+1]-=s-a[i],cnt++;if(a[i]>s) a[i+1]+=a[i]-s,cnt++;a[i]=s;}std::cout<<cnt<<'\n';
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}

122. 糖果传递 - AcWing题库

n个小朋友坐一圈，每人只能给左右两人传递糖果。 

这题跟上面唯一的不同就在于，围成了一个圈。我们想想上一题递推的突破口是什么呢？是1！因为只有2跟他换。对于这个问题能不能破环成链呢？

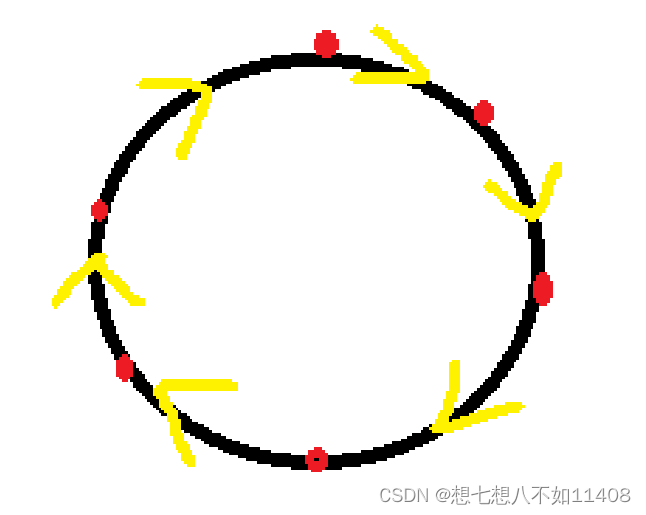
我们为什么需要这样一个接一个的传递糖果？因为糖果只能给相邻的小朋友，我要把多的移走对吧。

倘若盯着一个人看，让它当第一个操作的人。我刚把糖果移走，你为什么要还给我？这样是不是说明做了无用功，因为给出去的糖果又回到我手上了！因此，势必有一个小孩得到/失去糖果之后就不再与别人操作了！那么，谁来当第一个交换的小孩呢？

举个栗子！

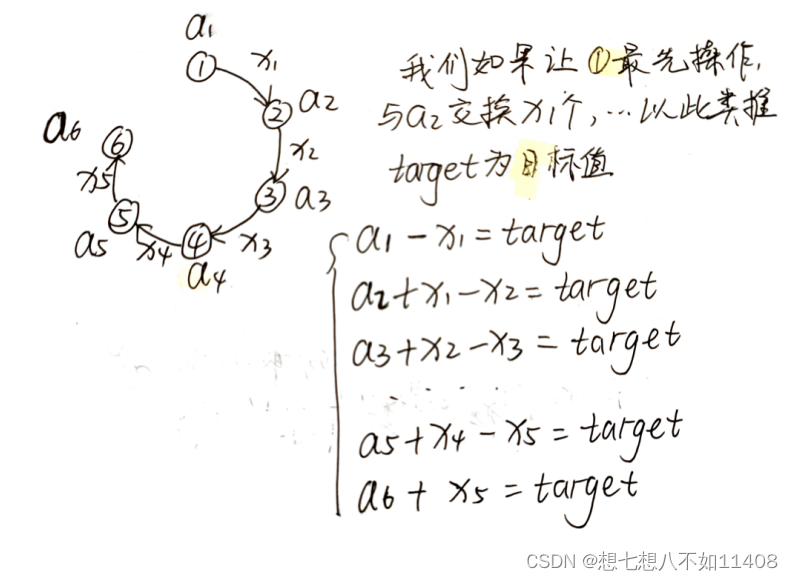
可以看到这个问题就转化成了绝对值求和的问题！抽象成了一个数学问题，也就是x1取ci中位数的时候能够有最小值sum。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e6+10;
const int mod=1e9+7;
int a[N],sum[N];
int n;
ll s=0,cnt;
void solve()
{std::cin>>n;for(int i=1;i<=n;i++){std::cin>>a[i];s+=a[i];}s/=n;for(int i=1;i<=n;i++){a[i]-=s;sum[i]=sum[i-1]+a[i];//公式里的c数组 }std::sort(sum+1,sum+1+n);int mid=n/2+1;//中位数for(int i=1;i<=n;i++){cnt+=std::abs(sum[mid]-sum[i]);	} std::cout<<cnt<<'\n';
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}

105. 七夕祭 - AcWing题库

布置场地，让每行感兴趣的摊点数一样多，每列感兴趣的摊点数一样多。同手每行/每列第一个和最后一个位置算做相邻。求解交换两个摊点的最少次数。

首先看到”算做相邻“，”均摊“很容易想到上面的环形均摊纸牌的算法对吧。但是这题不同点在于，对每行每列都有要求。 但是，当我们交换两个摊点的时候，只会改变要么行要么列的状态。左右交换的时候，只会改变这两列的点数。上下交换的时候，只会改变这两行的点数。因此，我们把这个问题分割成两个。左右交换的最少次数，和上下交换的最少次数。这样就又变成了上面的糖果传递问题。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
const int mod=1e9+7;
int row[N],col[N],sr[N],sl[N];
int n,m,s;
ll cnt1=-1,cnt2=-1;
void solve()
{std::cin>>n>>m>>s;for(int i=1;i<=s;i++){int x,y;std::cin>>x>>y;row[x]++,col[y]++;}if(s%n==0)//对行 {cnt1=0;int t=s/n;for(int i=1;i<=n;i++){row[i]-=t;sr[i]=sr[i-1]+row[i];	}  std::sort(sr+1,sr+1+n);int mid=1+n/2;for(int i=1;i<=n;i++){cnt1+=std::abs(sr[i]-sr[mid]);}}if(s%m==0)//对列{cnt2=0;int t=s/m;for(int i=1;i<=m;i++){col[i]-=t;sl[i]=sl[i-1]+col[i];	}  std::sort(sl+1,sl+1+m);int mid=1+m/2;for(int i=1;i<=m;i++){cnt2+=std::abs(sl[i]-sl[mid]);}}if(cnt1==-1&&cnt2==-1){std::cout<<"impossible"<<'\n';}else{if(cnt1!=-1&&cnt2!=-1){std::cout<<"both"<<' ';std::cout<<cnt1+cnt2<<'\n';}else if(cnt1!=-1){std::cout<<"row"<<' ';std::cout<<cnt1<<'\n';}else{std::cout<<"column"<<' ';std::cout<<cnt2<<'\n';}}
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}

写进一个函数里。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
const int mod=1e9+7;
int row[N],col[N],sr[N];
int n,m,s;
ll cnt1,cnt2;
ll calc(int nn,int h[])
{ll cnt=-1;if(s%nn==0){cnt=0;int t=s/nn;for(int i=1;i<=nn;i++){h[i]-=t;sr[i]=sr[i-1]+h[i];	}  std::sort(sr+1,sr+1+nn);int mid=1+nn/2;for(int i=1;i<=nn;i++){cnt+=std::abs(sr[i]-sr[mid]);}}return cnt;
}
void solve()
{std::cin>>n>>m>>s;for(int i=1;i<=s;i++){int x,y;std::cin>>x>>y;row[x]++,col[y]++;}cnt1=calc(n,row);cnt2=calc(m,col);if(cnt1==-1&&cnt2==-1){std::cout<<"impossible"<<'\n';}else{if(cnt1!=-1&&cnt2!=-1){std::cout<<"both"<<' ';std::cout<<cnt1+cnt2<<'\n';}else if(cnt1!=-1){std::cout<<"row"<<' ';std::cout<<cnt1<<'\n';}else{std::cout<<"column"<<' ';std::cout<<cnt2<<'\n';}}
}
signed main()
{std::ios::sync_with_stdio(false);std::cin.tie(0);int t=1;//std::cin>>t;while(t--){solve();}return 0;
}