一、单项选择题
01.图中有关路径的定义是()。
A.由顶点和相邻顶点序偶构成的边所形成的序列 B.由不同顶点所形成的序列
C.由不同边所形成的序列 D.上述定义都不是
02.一个有n个顶点和n条边的无向图一定是( )。
A.连通的 B.不连通的 C.无环的 D.有环的
03.若从无向图的任意顶点出发进行一次深度优先搜索即可访问所有顶点,则该图一定是
( )。
A.强连通图 B.连通图 C.有回路 D.一棵树
04.以下关于图的叙述中,正确的是( )。
A.图与树的区别在于图的边数大于或等于顶点数
B.假设有图G={V,{E}},顶点集,则V'和{E'}构成G的子图
C.无向图的连通分量是指无向图中的极大连通子图
D.图的遍历就是从图中某一顶点出发访遍图中其余顶点
05.以下关于图的叙述中,正确的是( )。
A.强连通有向图的任何顶点到其他所有顶点都有弧
B.图的任意顶点的入度等于出度
C.有向完全图一定是强连通有向图
D.有向图的边集的子集和顶点集的子集都构成原有向图的子图
06.一个有28条边的非连通无向图至少有()个顶点。
A.7 B.8 C.9 D.10
07.对于一个有n个顶点的图:若是连通无向图,其边的个数至少为(),若是强连通有向图,则其边的个数至少为().
A. n-1,n B. n-1, n(n-1) C. n, n D.n, n(n-1)
08.无向图G有23条边,度为4的顶点有5个,度为3的顶点有4个,其余都是度为2的
顶点,则图G有( )个顶点。
A.11 B. 12 C. 15 D.16
09.在有n个顶点的有向图中,顶点的度最大可达() 。
A. n B. n-1 C. 2n D. 2n-2
10.具有6个顶点的无向图,当有()条边时能确保是一个连通图。
A.8 B.9 C. 10 D.11
11.设有无向图G=(V,E)和G'=(V,E'),若G是G的生成树,则下列不正确的是()。
Ⅰ.G'为G的连通分量
Ⅱ.G'为G的无环子图
Ⅲ.G'为G的极小连通子图且V'=V
A.I、Ⅱ B.只有Ⅲ C.Ⅱ、Ⅲ D.只有Ⅰ
12.具有51个顶点和21条边的无向图的连通分量最多为( )。
A. 33 B.34 C. 45 D.32
13.在如下图所示的有向图中,共有()个强连通分量。
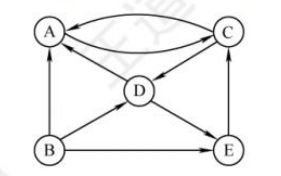
A. 1 B.2 C.3 D.4
14.若具有n个顶点的图是一个环,则它有()棵生成树。
A. n^2 B.n C. n-1 D.1
15.若一个具有n个顶点、e条边的无向图是一个森林,则该森林中必有( )棵树。
A. n B. e C. n-e D.1
16.【2009统考真题】下列关于无向连通图特性的叙述中,正确的是()。
Ⅰ所有顶点的度之和为偶数
Ⅱ.边数大于顶点个数减1
Ⅲ.至少有一个顶点的度为1
A.只有Ⅰ B.只有Ⅱ C.I和Ⅱ D.Ⅰ和Ⅲ
17.【2010统考真题】若无向图G=(V, E)中含有7个顶点,要保证图G在任何情况下都是连通的,则需要的边数最少是()。
A. 6 B.15 C.16 D.21
18.【2017统考真题】已知无向图G含有 16条边,其中度为4的顶点个数为3,度为3的
顶点个数为4,其他顶点的度均小于3。图G所含的顶点个数至少是( )。
A.10 B.11 C.13 D.15
19.【2022统考真题】对于无向图G=(V,E),下列选项中,正确的是().
A.当|V|>|E|时,G一定是连通的
B.当|V|<|E|时,G一定是连通的
C.当|V|=|E|-1时,G一定是不连通的
D.当|V|>|E|+1时,G一定是不连通的