题目来源:https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/

C++题解(思路来源代码随想录):动态规划
- 确定dp数组(dp table)以及下标的含义。dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。
- 递推公式:当A[i - 1] 和B[j - 1]相等的时候,dp[i][j] = dp[i - 1][j - 1] + 1;
- 确定遍历顺序。这步在我这是最难的,因为不知道怎么实现,直到看到下面的图。其实本质上还是两个for循环,只是用的[i-1][j-1],走的是斜线,不是直线下来。因此,初始化时,第一行跟第一列都为0
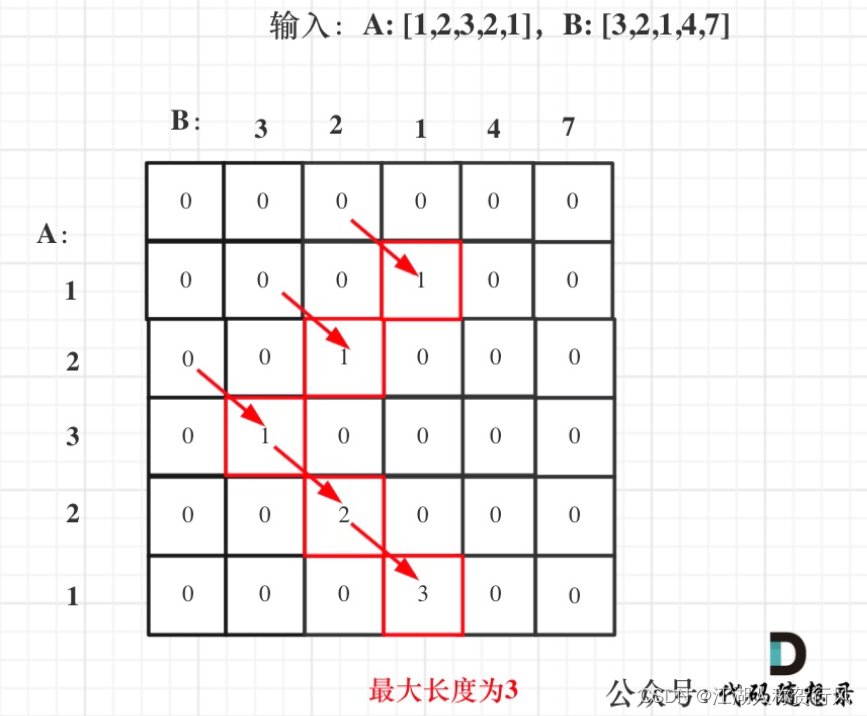
上代码:
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int n1 = nums1.size(), n2 = nums2.size();// dp[i][j]表示nums1[i-1]与nums2[j-1] 公共的、长度最长的子数组长度// 动归更新条件为nums1[i]==nums2[j], dp[i][j] = dp[i-1][j-1] + 1vector< vector<int>> dp(n1+1, vector<int>(n2+1, 0));int result = 0;for(int i = 1; i <= n1; i++) {for(int j = 1; j <= n2; j++) {if(nums1[i-1] == nums2[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;result = max(result, dp[i][j]);}}}return result;}
};