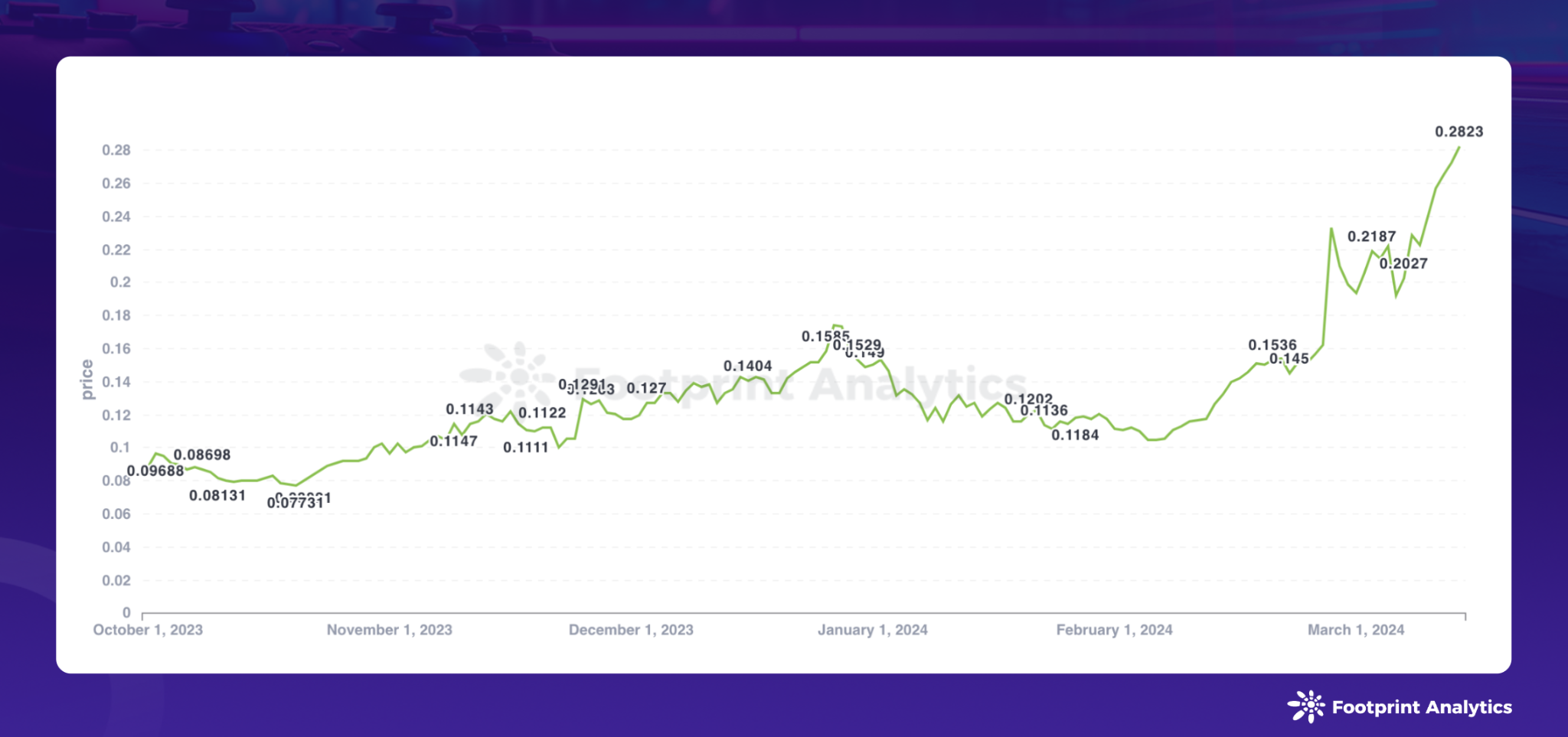
头文件：#include<queue>

内部使用堆来实现，在需要或得最大的几个值或最小的几个值而不关心整个数组的顺序时非常好用。

用法：

priority_queue<int, vector<int>, greater<int>>q;
第一个参数为堆中存储的元素。

第二个参数为底层使用的存储结构，默认使用vector。

第三个参数为优先队列中元素的比较方式的类。如果是小根堆则为greater，大根堆为less；less、greater二者为仿函数，即把类当作函数使用，本质上为类，内部重载了()运算符，所以可以当作函数。

如果堆中存储的是int元素，则只需要传入less或greater即可，less<T>来定义大顶堆，
greater<T>来定义小顶堆，不需要我们手动实现。

如果传入的是其他复杂类型，则需要我们手动实现比较类。

参考下面这篇文章：

http://t.csdnimg.cn/04qeZ

lambda表达式的详细信息可参考下面这篇：http://t.csdnimg.cn/42OXw

刷题时遇到一道题，

给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k 。

定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2 。

请找到和最小的 k 个数对 (u1,v1),  (u2,v2)  ...  (uk,vk) 。

暂未想到合适的解决方案，刚好这题在堆这一章里面，于是考虑使用堆实现。

class cmp
{
public:bool operator()(pair<int,int>&p1,pair<int,int>&p2){return p1.first+p1.second<p2.first+p2.second;}
};class Solution {
public:vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {priority_queue<pair<int,int>,vector<pair<int,int>>,cmp>q;vector<vector<int>>res;for(int i=0;i<nums1.size();i++){for(int j=0;j<nums2.size();j++){if(q.size()<k)q.push(make_pair(nums1[i],nums2[j]));else if(nums1[i]+nums2[j]<q.top().first+q.top().second){q.pop();q.push(make_pair(nums1[i],nums2[j]));}}}while(k--){vector<int>temp;temp.push_back(q.top().first);temp.push_back(q.top().second);res.push_back(temp);q.pop();}return res;}
};

大顶堆小顶堆巧记：在cmp判断函数中，总是返回右边的，即p2。如果是>，则右边较小，为小顶堆。如果是<，则右边较大，为大顶堆。

上述代码中就是使用了大顶堆，大顶堆的数量不超过k，当来了一个新的元素对，将该元素对之和与堆顶元素之和作比较，如果小于堆顶元素之和，说明堆顶还不是最小的k个之一，将堆顶弹出，插入当前元素对。

注：关于pair：函数定义时参数使用pair<int, int>& p1。使用p1.first , p1.second来获取其中的元素。使用pair<int,int>p=make_pair(q.top().first,q.top().second);，也可以直接将make_pair传入函数参数中。

虽然最后只通过了20/30的测试用例，但在数据量较小时也不失为一种方法，且对priority_queue以及函数对象、lambda表达式有了更深刻的认识。

也可以使用lambda表达式：

        auto cmp=[](pair<int,int>&p1,pair<int,int>&p2){return p1.first+p1.second<p2.first+p2.second;};priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(cmp)>q(cmp);

上述题目正解：

class Solution {
public:vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {auto cmp = [&nums1, &nums2](const pair<int, int> & a, const pair<int, int> & b) {return nums1[a.first] + nums2[a.second] > nums1[b.first] + nums2[b.second];};int m = nums1.size();int n = nums2.size();vector<vector<int>> ans;   priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);for (int i = 0; i < min(k, m); i++) {pq.emplace(i, 0);}while (k-- > 0 && !pq.empty()) {auto [x, y] = pq.top(); pq.pop();ans.emplace_back(initializer_list<int>{nums1[x], nums2[y]});if (y + 1 < n) {pq.emplace(x, y + 1);}}return ans;}
};

整体思路相似，都是使用堆。不过该程序堆存储的是数组的索引，便于获得后面索引的值。

在一开始时将0,0  1,0  2,0  3,0......i,0加入堆。每次出堆时，仅仅将i,j+1入堆（事实上i,j入堆下一个可能最小的是i+1,j或i,j+1，但是如果二者都入堆有可能出现重复，即i+1,j+1重复入堆。所以一开始将0,j全部入堆，每次出堆时仅将i，j+1入堆即可，直到结果集中有k个元素。）