目录

常见比较检验方法

总述

2.4.1 假设检验

2.4.2 交叉验证T检验

2.4.3 McNemar 检验

---

接我们的上一篇《性能度量》，那么我们在某种度量下取得评估结果后，是否可以直接比较以评判优劣呢？实际上是不可以的。因为我们第一，测试性能不等于泛化性能，第二，测试性能会随着测试集的变化而变化，第二，很多机器学习算法本身有一定的随机性，即便用相同参数设置在同一测试集上其结果也会不同所以直接选取相应评估方法在相应度量下比大小的方法不可取。

常见比较检验方法

统计假设检验 (hypothesis test) 为学习器性能比较提供了重要依据。即比较两算法性能是否相同。一般我们假设两算法性能一样，很显然，若拒绝，则性能不一样，若没拒绝则性能一样。（参见《概率论与数理统计》中假设检验）

两学习器比较：

1.交叉验证 t 检验 (基于成对 t 检验) k 折交叉验证； 5x2交叉验证

2.McNemar 检验 (基于列联表，卡方检验)

多学习器比较：

1.Friedman检验 (基于序值，F检验; 判断“是否都相同”)

2.Nemenyi 后续检验 (基于序值，进一步判断两两差别)

总述

首先我们比较两个学习器的时候，假设我们两学习器一样的性能，我们基于一个值来评估，那么我们在多个测试集中得出的两学习器的误差的差的均值近似为0.显然我们判断此种情况时符合我们的T检验。对于我们的多个值评估，我们使用联列表（记得上次那个TP,NP的表吗？这就类似于那个）假设我们有两个学习器，对于同一组样本，我们的联列表如下：

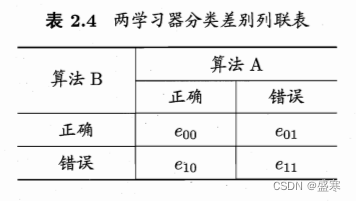
显然，我们对比副对角线（即代表算法A和B认为的“差异”部分），并对此进行检验分布。

2.4.1 假设检验

在分析交叉验证t检验之前我们先来分析一下二项检验。题目如下：

这个题目可能有点难以理解，我们换个题目：

假设我们有一个球堆A，里面有一些黑球和白球，我们拿m次球，拿到的黑球有m*p个，随后我们又在球堆B里拿球，球堆有m0个球，我们拿到黑球的概率是P2，请问我们恰好有m*p次拿到黑球的概率是多少？

这道题我们只看后面的部分，即：在球堆B里拿球，球堆有m个球，我们拿到黑球的概率是P2，请问我们恰好有m*p次拿到黑球的概率是多少？

显然我们使用二项分布，即C（m*p ，m0）* P2的m*p次方 * (1-P2）的（m0-m*p）次方。

我们回到之前的题目中，是否有些相似了呢？

泛化错误率就是我们这里的P2，测试错误率就是我们这里的p，m和m0分别对应我们这里的m和m0.

类比思考一下，我们就能很轻松的得到以下式子：其表达的含义为：在m个样本上，泛化错误率被测得为测试错误率的概率。（这里的括号与C的含义相同但是上下颠倒），显然我们这里符合二项分布。

随后我们使用极大似然估计（可以参考《概率论与数理统计一书》），得到其概率在 ^时最大。

我们假设ϵ=0.3,m=10，我们可得到以下的图：

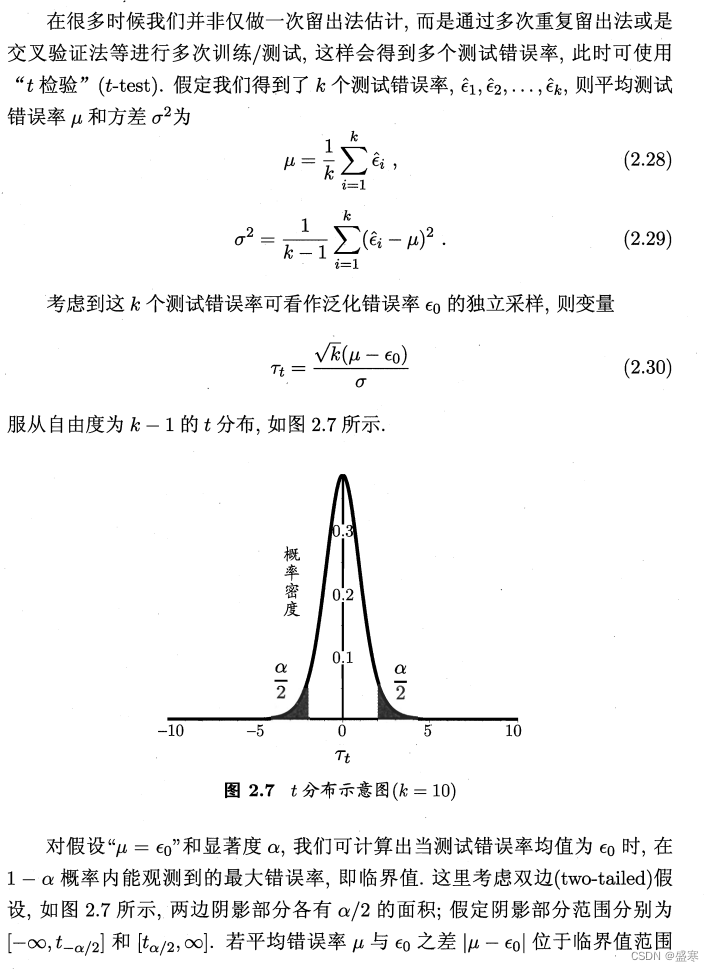
这里t分布与之前的二项分布有相似之处，可以结合起来一起理解。

2.4.2 交叉验证T检验

2.4.3 McNemar 检验

其使用的卡方分布，但同样的使用的统计学理念与之前类似。

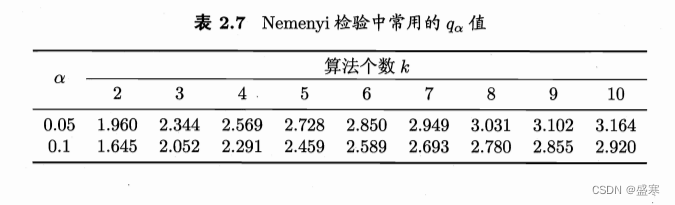
2.4.4 Friedman检验与Nemenyi后续检验