地下城游戏
- 1. 题目解析
- 2. 讲解算法原理
- 3. 编写代码
1. 题目解析
题目地址:点这里

2. 讲解算法原理
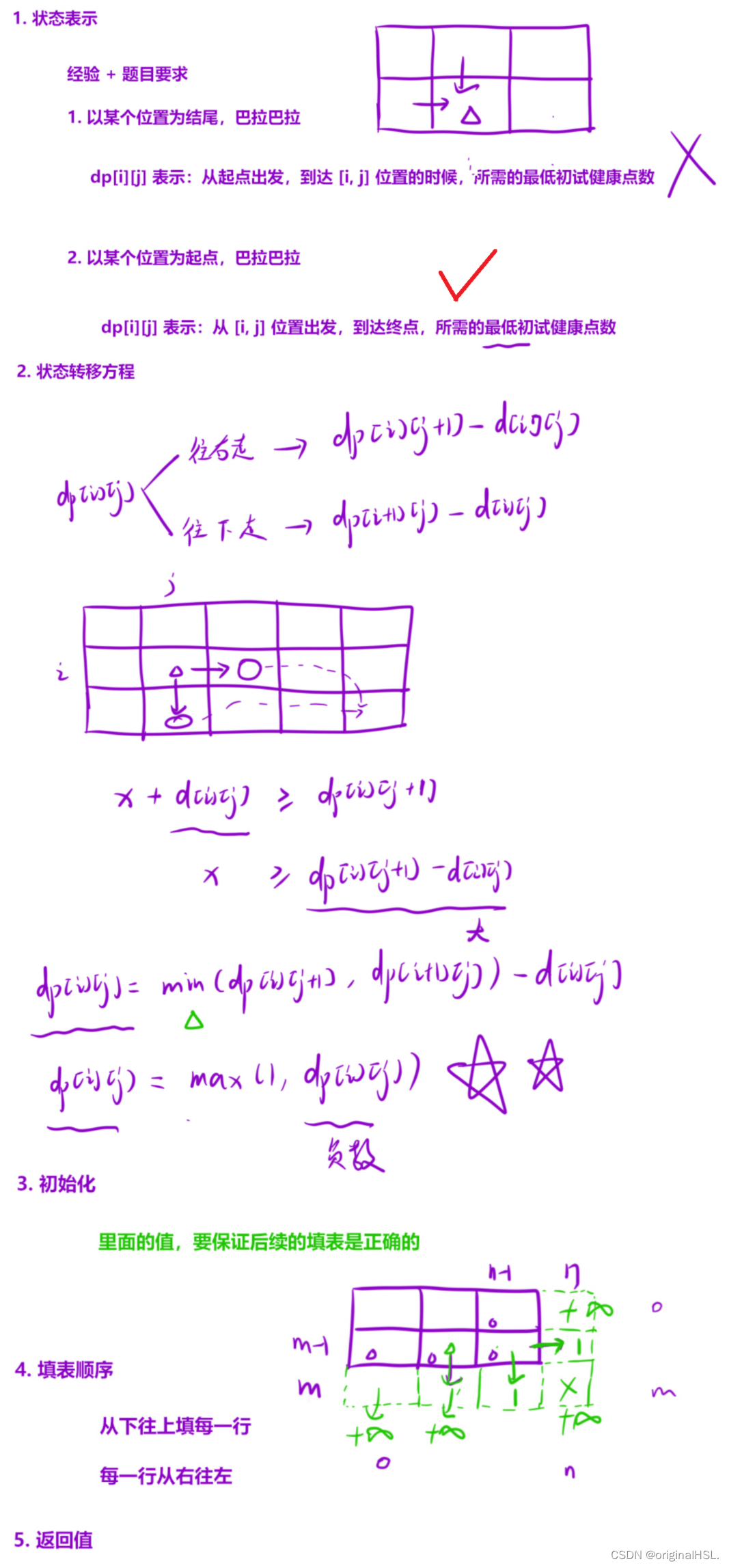

-
首先,定义一个二维数组 dp,其中 dp[i][j] 表示从位置 (i, j) 开始到达终点时的最低健康点数。
-
初始化数组 dp 的边界条件:
- 对于最后一行,即 dp[m-1][j](其中 m 是行数),表示最后一行的每个位置到达终点时的最低健康点数。由于只能向右移动,所以从最后一行的任意位置出发都必须向右移动到达终点,因此初始化为 1。
- 对于最后一列,即 dp[i][n-1](其中 n 是列数),表示最后一列的每个位置到达终点时的最低健康点数。由于只能向下移动,所以从最后一列的任意位置出发都必须向下移动到达终点,因此初始化为 1。
-
初始化除了最后一行和最后一列之外的其他位置 dp[i][j] 的值为正无穷大(INT_MAX),表示无法到达终点。
-
从倒数第二行开始,从右往左,从下往上遍历整个地牢。对于每个位置 (i, j),计算到达终点的最低健康点数:
- 使用状态转移方程 dp[i][j] = min(dp[i][j+1], dp[i+1][j]) - dungeon[i][j],表示选择向右移动和向下移动中所需最低健康点数较小的那个,并减去当前位置的健康点数消耗。
- 对于 dp[i][j] 的值,还需要确保其不会小于 1,因为健康点数不能为负数。
- 最后,返回 dp[0][0],即起点位置的最低健康点数。
3. 编写代码
class Solution {
public://状态表示:以i位置为起点,到达终点时的最低健康点数(此题以i位置为结尾解不出来!!!)int calculateMinimumHP(vector<vector<int>>& dungeon) {int m=dungeon.size();int n=dungeon[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1));dp[m-1][n]=1,dp[m][n-1]=1;for(int i=0;i<n-1;i++) dp[m][i]=INT_MAX;for(int j=0;j<m-1;j++) dp[j][n]=INT_MAX;for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){//状态转移方程!!!!dp[i][j]=min(dp[i][j+1],dp[i+1][j])-dungeon[i][j];dp[i][j]=max(1,dp[i][j]);}}return dp[0][0];}
};