相机系列文章是用来记录使用opencv3来完成单目相机和6轴机械臂手眼标定。本人吃饭的主职是linux下6轴机械臂相关应用开发。但对于机械臂运动学、相机应用等都非常感兴趣，所以对一些线性代数基础薄弱又想深入了解机械臂内部运算的同志比较有体会。由于是探索性学习，所以文章并没有太多规律而言，更像是技术路线调整，但这更贴近实际。探索事物本质是快乐的，强者不是天生的，而是学习思考来的。

最近参与了3D相机应用项目，与同事交流下又对机械臂运行学有了新的理解，像是一层窗户纸被捅破了，最终感觉就是算矩阵。

一、相机四个坐标系

世界坐标系、相机坐标系、图像坐标系、像素坐标系。

相机将三维世界中的坐标点(单位是m)映射到二维图像平面(单位为像素)的过程可用一个几何模型进行描述。模型有很多种，最简单的是针孔模型，即小孔成像。

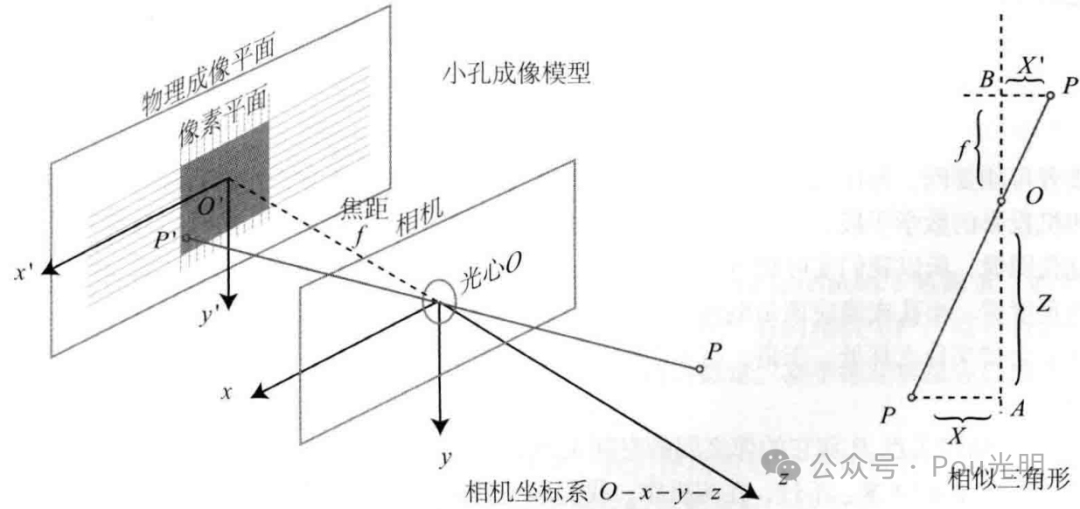
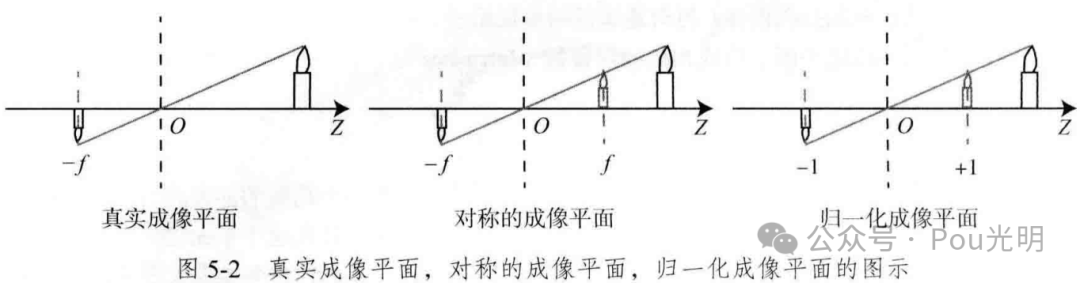
上图中O为相机的光心，也是针孔模型中的针孔。现实世界的空间点P，经过小孔O投影后，落在物理成像平面O’-x’-y’上，成像点为P’。设P的坐标位[X, Y, Z]T，P’为[X’, Y’, Z’]T，设物理成像平面到小孔的距离为f(焦距)，则根据三角形相似，得    

Z/f = -X/X’ = -Y/Y’

其中负号代表成像是倒立的。但实际应用中图像并不是倒像(否则相机的使用会非常不便)。为了让模型更符合实际，可以等价的将成像平面对称的放在相机前方，和三维空间点一起放在相机坐标系的同一侧。如图，这样可以将公式中负号去掉，则：

Z/f = X/X’ = Y/Y’                                                      ......(1)式

整理得：

X’ = fX/Z

Y’ = fY/Z

上式描述了P点和它成像之间的空间关系，这里所有单位都可以理解成米。但在相机中我们获得的是一个个的像素，所以还需要进一步转换。

##1、像素坐标系

设在成像平面上像素坐标系o-x-y，则在像素平面得到P’的像素坐标：[u, v]T。

像素坐标系通常定义为：原点o’位于图像左上角，u轴向右与x轴平行，v轴向下与y轴平行，则像素坐标系与成像平面之间相差一个缩放与一个原点平移。设像素坐标在u轴上缩放α倍，在u轴上缩放β倍；原点平移了[cx, cy]T，则P’(图像坐标)坐标与像素坐标[u, v]的关系为：

u = αX’ + cx    

v = βY’ + cy

与(1)式联立，令αf为fx，βf为fy，得

u = αfxX/Z + cx

v = βfyY/Z + cy

上式f单位为m，α和β单位为像素/米，则fx、fy、cx、cy的单位为像素。将上式携程矩阵形式，左侧是齐次坐标，右侧是非齐次：

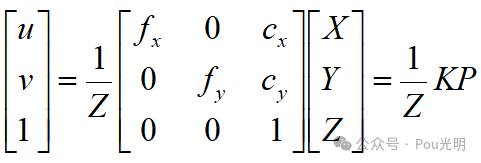
则：

   

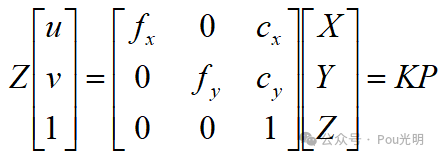
让人快乐的消息是中间这个3×3矩阵正是被称为相机内参的矩阵。通常认为相机内参在出厂后㐊固定的，不会再使用过程中发生变化。

OK，接下来就是外参。上式中P的坐标是基于相机坐标系的，但实际上由于相机在运动，所以P的相机坐标应该是它的世界坐标(Pw)根据相机当前的姿态变换到相机坐标系下的结果。相机位姿由它的旋转矩阵和R和平移矩阵t来描述(这块之后再细说)。则：

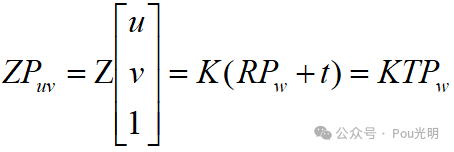
注意后式隐含了一次齐次到非齐次的转换(么看出来)。它描述了P的世界坐标到相机坐标的投影关系。其中，相机的位姿R,t又称为相机的外参数。相比不变的内参，外参会随着相机的运动发生改变。    

《视觉SLAM十四讲》第二版，P123

注意： 本内容仅用作个人学习，勿用作商业用途

欢迎关注，记录学习！