文章目录
- 📝希尔排序( 缩小增量排序 )
- 🌠分组思想
- 🌠缩小增量的过程
- 🌠 排序步骤
- 🌉希尔排序的特性总结:
- 🚩总结
📝希尔排序( 缩小增量排序 )
希尔排序是一种经典的排序算法,它通过多次插入排序的方式,以及逐步缩小增量的策略,实现对数据的高效排序,希尔排序法又称缩小增量法。
🌠分组思想
希尔排序的核心思想在于将待排序的数据分成若干组,对每一组数据进行插入排序。这样做的好处是,一方面可以减少数据的比较次数和移动次数,另一方面可以利用已经部分有序的性质,加速排序的过程。初始时,数据被分成的组数由一个称为增量的值决定。
🌠缩小增量的过程
希尔排序的另一个关键点是逐步缩小增量的过程。初始时,增量的值通常为数组长度的一半。随着排序的进行,增量逐步减小,直到增量为1,完成最后一次排序。这样的设计可以使得排序过程更加高效,因为随着增量的减小,每次排序所需要的数据交换次数会逐渐减少。
🌠 排序步骤
希尔排序的排序步骤可以分为以下几个阶段:
分组排序:初始时,根据设定的增量将数据分成若干组,对每组数据进行插入排序,使得每组数据都部分有序。
逐步缩小增量:在每一轮排序后,逐步减小增量的值,重新分组并进行插入排序,直到增量为1。
最后一次排序:当增量为1时,整个数组被视为一组,对整个数组进行插入排序,使得整个数组有序。
图解:
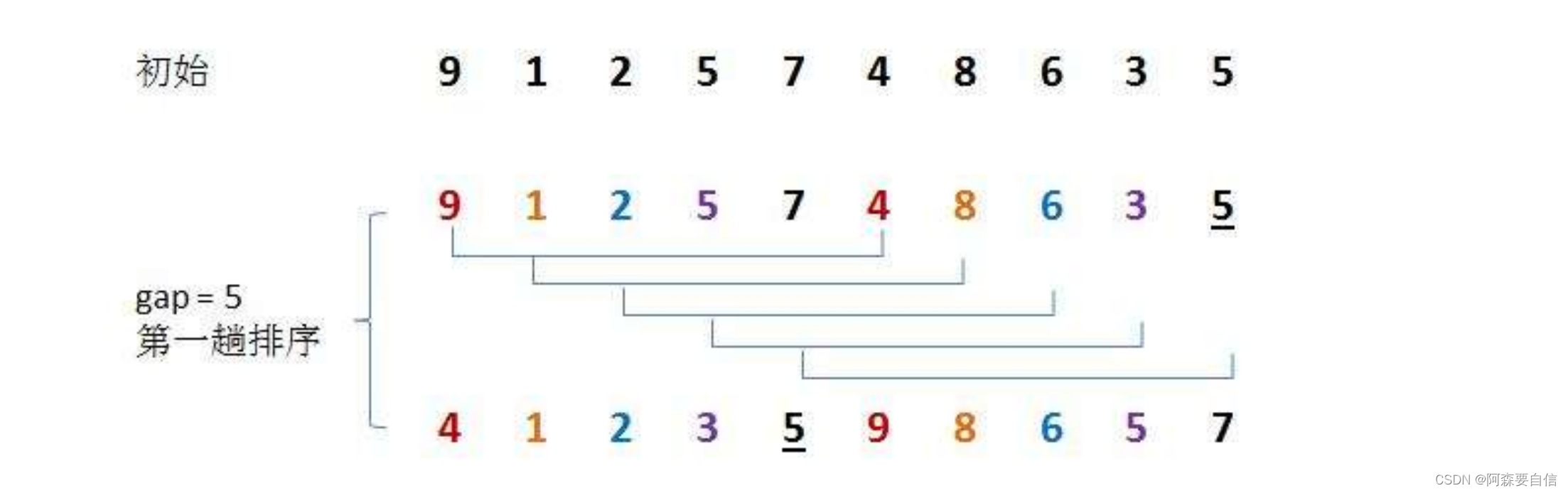
代码实现:
// 预排序 -- 目标:接近有序 gap > 1
// 插入排序 -- 目标:有序 gap == 1
// O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap /= 2;gap = gap/3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
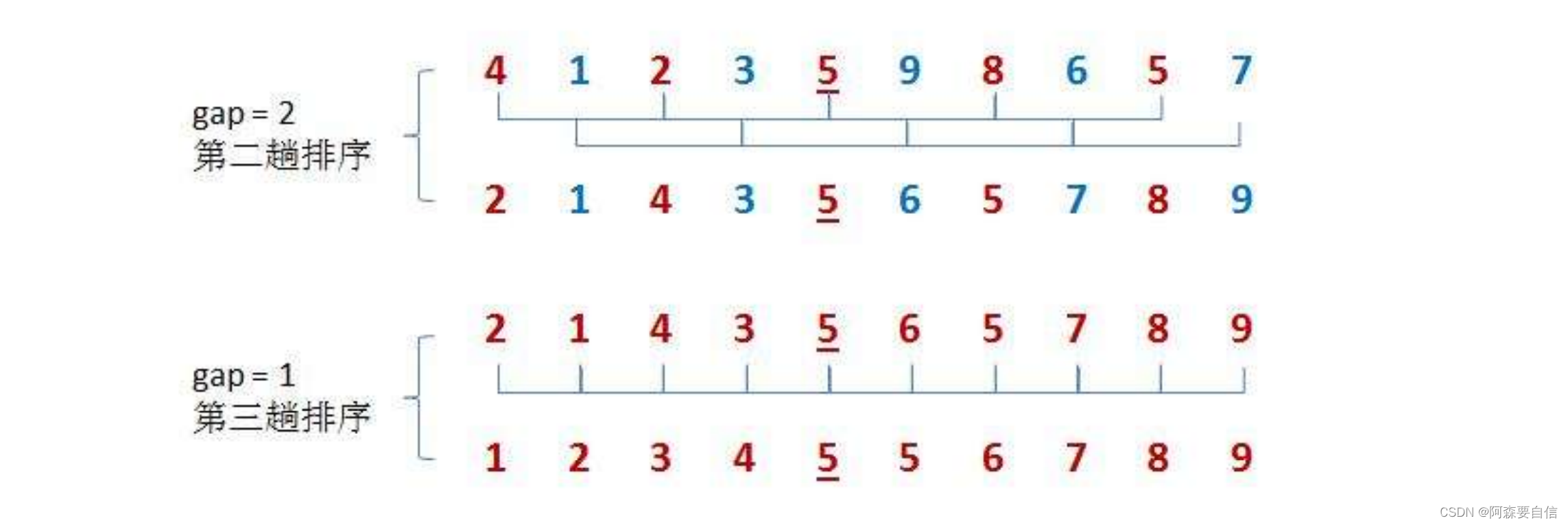
图解三趟:


🌉希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
时间复杂度分析: O(N^1.3),相比于普通的插入排序有较大的优化。
空间复杂度分析:的空间复杂度为 O(1),即不需要额外的存储空间。
排序稳定性分析:不稳定,即在排序过程中相等元素的相对位置可能发生变化。
🚩总结
希尔排序法的基本思想:
先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序
时间复杂度
O(N^1.3)
空间复杂度的空间复杂度为 O(1)
排序稳定性:不稳定,即在排序过程中相等元素的相对位置可能发生变化。









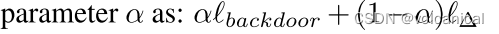



![[Linux初阶]which-find-grep-wc-管道符命令](https://img-blog.csdnimg.cn/direct/a9e0a7c460434f44a967d3748fc7ca97.png)