神经网络与深度学习（一）

线性回归

定义

利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法

要素

训练集（训练数据）
输出数据
拟合函数
数据条目数

场景

预测价格（房屋、股票等）、预测住院时间（针对住院病人等）、预测需求（零售销量等）

实例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split 
from sklearn.linear_model import LinearRegression
from sklearn import metrics# 创建一些随机的线性数据
np.random.seed(0)
x = np.random.rand(100, 1)
y = 2 + 3 * x + np.random.rand(100, 1)# 将数据分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)# 创建线性回归模型
regressor = LinearRegression()  # 使用训练数据来训练模型
regressor.fit(x_train, y_train) # 使用测试数据来评估模型
y_pred = regressor.predict(x_test)# 计算模型的准确度
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))  
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))  
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))# 绘制原始数据和拟合的直线
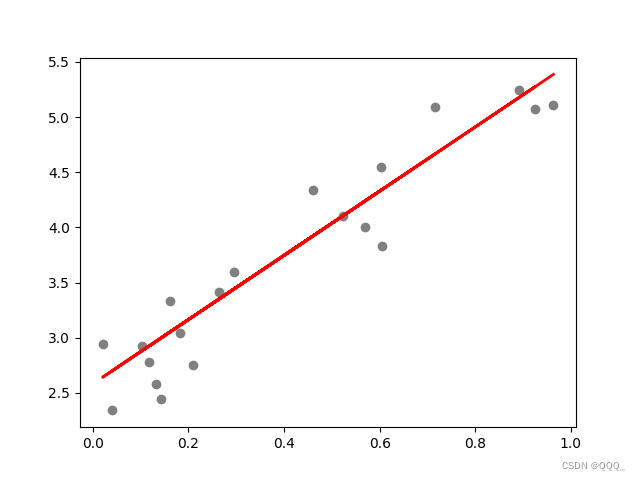
plt.scatter(x_test, y_test,  color='gray')
plt.plot(x_test, y_pred, color='red', linewidth=2)
plt.show()

线性回归

分类与回归

线性二分类

定义

线性分类器则透过特征的线性组合来做出分类决定，以达到此种目的。简言之，样本通过直线(或超平面)可分。

线性分类器输入：特征向量
输出：哪一类。如果是二分类问题，则为0和1，或者是属于某类的
概率：即0-1之间的数。

线性分类与线性回归差别

输出意义不同：属于某类的概率VS回归具体值
参数意义不同：最佳分类直线VS最佳拟合直线
维度不同：一维的回归VS二维的分类

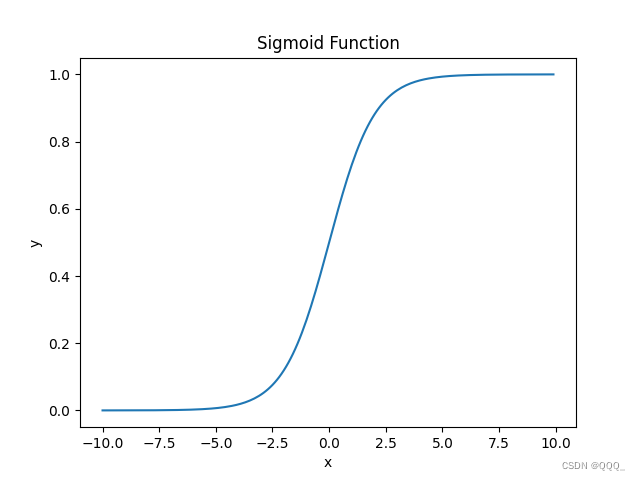
Sigmoid函数

用于结果转换，归入0-1区间

梯度下降法

梯度下降法（Gradient Descent）是一种用于找到函数局部极小值的优化算法。它通过向函数上当前点对应梯度的反方向迭代搜索，以寻找最小值。如果相反地向梯度正方向迭代搜索，则会接近函数的局部极大值点，这个过程被称为梯度上升法。

二分类实例

import numpy as np
import matplotlib.pyplot as plt# 设定随机种子以便结果可复现
np.random.seed(0)# 生成数据集
X = np.random.randn(100, 2)  # 生成100个样本，每个样本有2个特征
Y = np.where(X[:, 0] + X[:, 1] > 0, 1, 0)  # 根据线性方程生成标签# 绘制原始数据
plt.scatter(X[Y == 0][:, 0], X[Y == 0][:, 1], color='red', label='Class 0')
plt.scatter(X[Y == 1][:, 0], X[Y == 1][:, 1], color='blue', label='Class 1')
plt.legend()
plt.title('Original Data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()# 梯度下降函数
def gradient_descent(X, Y, theta, alpha, iterations):m = len(X)for i in range(iterations):h = np.dot(X, theta)loss = h - Ygradient = np.dot(X.transpose(), loss) / mtheta = theta - alpha * gradientreturn theta# 初始化参数
theta = np.zeros(2)  # 特征数量 + 截距项
alpha = 0.01  # 学习率
iterations = 1000  # 迭代次数# 运行梯度下降
theta = gradient_descent(X, Y, theta, alpha, iterations)# 绘制决策边界
def plot_decision_boundary(theta, X, Y):x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1h = (theta[0] * x_min + theta[1] * y_min) / -theta[2]k = -theta[0] / theta[1]xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))Z = np.dot(np.array([xx.ravel(), yy.ravel()]), theta)Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.scatter(X[Y == 0][:, 0], X[Y == 0][:, 1], color='red', label='Class 0')plt.scatter(X[Y == 1][:, 0], X[Y == 1][:, 1], color='blue', label='Class 1')plt.legend()plt.title('Decision Boundary')plt.xlabel('X1')plt.ylabel('X2')plot_decision_boundary(theta, X, Y)
plt.show()

请添加图片描述

指数回归

实例

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit# 定义指数函数
def exponential_func(x, a, b, c):return a * np.exp(b * x) + c# 创建模拟数据
x = np.linspace(0, 4, 50)
y = 3 * np.exp(2.5 * x) + 0.5
np.random.seed(1729)
yn = y + 0.2 * np.random.normal(size=len(x))# 使用curve_fit进行拟合
popt, pcov = curve_fit(exponential_func, x, yn)# 输出最优参数
print("最优参数: ", popt)# 使用最优参数进行预测
y_pred = exponential_func(x, *popt)# 绘制原始数据和拟合曲线
plt.figure(figsize=(8, 6))
plt.scatter(x, yn, label='原始数据')
plt.plot(x, y_pred, 'r-', label='拟合曲线')
plt.legend()
plt.show()

请添加图片描述

多分类回归

多分类回归通常指的是多目标回归问题，即预测多个连续的输出变量。与多分类分类问题不同，回归任务预测的是连续的数值，而不是离散的类别。

实例

二分类

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler# 创建模拟的二分类数据集
np.random.seed(0)
X = np.random.randn(100, 2)  # 生成100个二维数据点
y = (X[:, 0] + X[:, 1] > 0).astype(int)  # 创建简单的线性分类标签# 使用逻辑回归（其输出层实际上应用了Softmax对于二分类）
# 对于多分类问题，我们可以使用LogisticRegression(multi_class='multinomial', solver='lbfgs')
clf = LogisticRegression(multi_class='multinomial', solver='lbfgs')
clf.fit(X, y)# 预测概率
probabilities = clf.predict_proba(X)# 绘制散点图
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k')# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
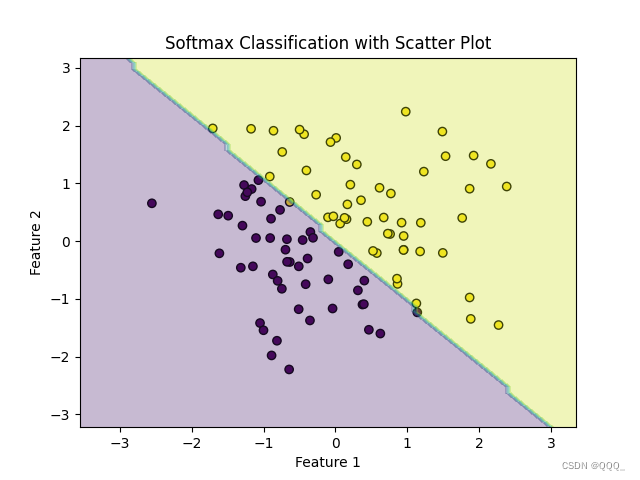
plt.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Softmax Classification with Scatter Plot')
plt.show()

请添加图片描述

多分类

import numpy as np
import matplotlib.pyplot as plt# 设置随机种子以保证结果的可复现性
np.random.seed(0)# 定义类别数量和每个类别的数据点数量
num_classes =5
num_points_per_class = 5000# 生成随机散点数据
X = np.zeros((num_classes * num_points_per_class, 2))
for i in range(num_classes):# 为每个类别生成一个正态分布的簇X[i * num_points_per_class: (i + 1) * num_points_per_class] = np.random.randn(num_points_per_class, 2) + [i, i]# 为每个类别创建一个权重向量和偏置项
W = np.random.randn(num_classes, 2)
b = np.random.randn(num_classes)# 计算每个数据点的分数
scores = np.dot(X, W.T) + b# 应用Softmax函数得到概率分布
def softmax(x):exps = np.exp(x - np.max(x, axis=1, keepdims=True))return exps / np.sum(exps, axis=1, keepdims=True)probabilities = softmax(scores)# 绘制散点图
colors = ['r', 'g', 'b', 'c', 'm']  # 每个类别的颜色
for i in range(num_classes):plt.scatter(X[scores[:, i] == np.max(scores, axis=1)][:, 0],X[scores[:, i] == np.max(scores, axis=1)][:, 1],c=colors[i], label=f'Class {i}')# 添加图例和坐标轴标签
plt.legend()
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
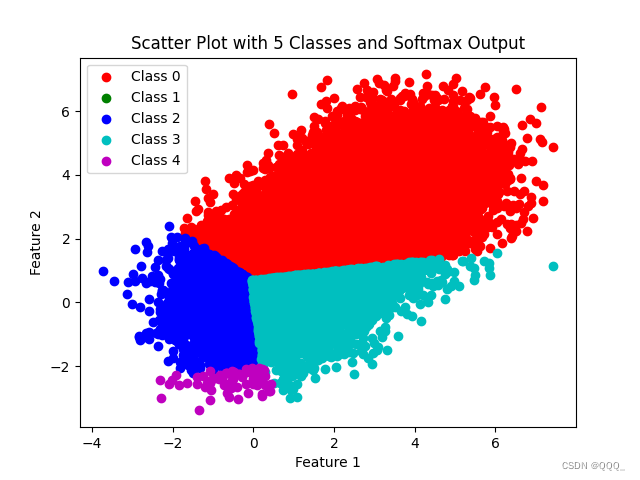
plt.title('Scatter Plot with 5 Classes and Softmax Output')# 显示图像
plt.show()# 打印Softmax概率（仅打印前5个数据点的概率作为示例）
print("Softmax Probabilities (for the first 5 points):")
print(probabilities[:5])

请添加图片描述

神经元模型

作用函数

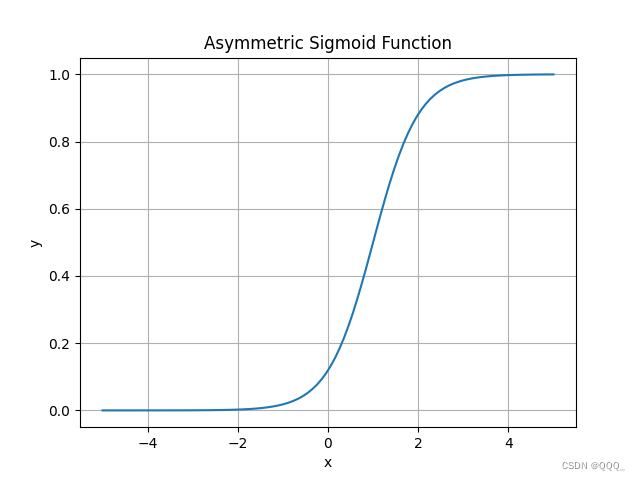
非对称型 Sigmoid 函数 (Log Sigmoid)

非对称型Sigmoid函数（也称作Log Sigmoid函数）是Sigmoid函数的一个变体，它可以将任何实数映射到介于0和1之间的值，但不像标准的Sigmoid函数那样是对称的。非对称型Sigmoid函数通常具有不同的形状参数，允许用户调整函数的形状以满足特定的需求。非对称型Sigmoid函数的一般形式可以表示为：f(x) = 1 / (1 + exp(-a * (x - b)))其中，a和b是形状参数。a控制函数的斜率，而b控制函数的中心位置。当a为正数时，函数在x=b处呈现出一个向上的S形曲线；当a为负数时，函数在x=b处呈现出一个向下的S形曲线。通过调整a和b的值，可以改变函数的形状和位置。

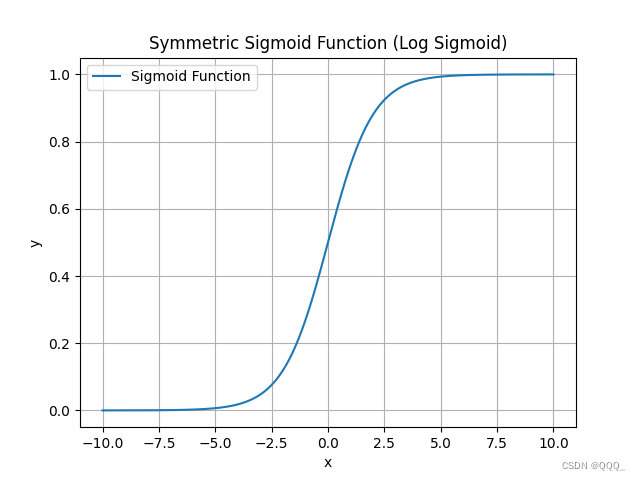
请添加图片描述

对称型 Sigmoid 函数 (Tangent Sigmoid）

对称型 Sigmoid 函数（也称为 Logistic Sigmoid 函数）是一种常用的非线性函数，通常用于将连续值映射到 0 到 1 之间的概率值。标准的对称型 Sigmoid 函数公式如下：
f(x) = 1 / (1 + exp(-x))
其中 exp 是自然指数函数，x 是输入值。这个函数将任何实数 x 映射到 (0, 1) 区间内，其中当 x 趋近于正无穷时，f(x) 趋近于 1；当 x 趋近于负无穷时，f(x) 趋近于0。
请添加图片描述

多层感知机

应对问题

线性不可分问题：无法进行线性分类。Minsky 1969年提出XOR问题
三层感知器可识别任一凸多边形或无界的凸区域。
更多层感知器网络，可识别更为复杂的图形。

实现过程

在输入和输出层间加一或多层隐单元，构成多层感知器（多层前馈神经网络）
加一层隐节点（单元）为三层网络，可解决异或（XOR）问题由输入得到两个隐节点、一个输出层节点的输出。

多层前馈网络

多层感知机是一种多层前馈网络，由多层神经网络构成，每层网络将输出传递给下一层网络。神经元间的权值连接仅出现在相邻层之间，不出现在其他位置。如果每一个神经元都连接到上一层的所有神经元（除输入层外），则成为全连接网络。

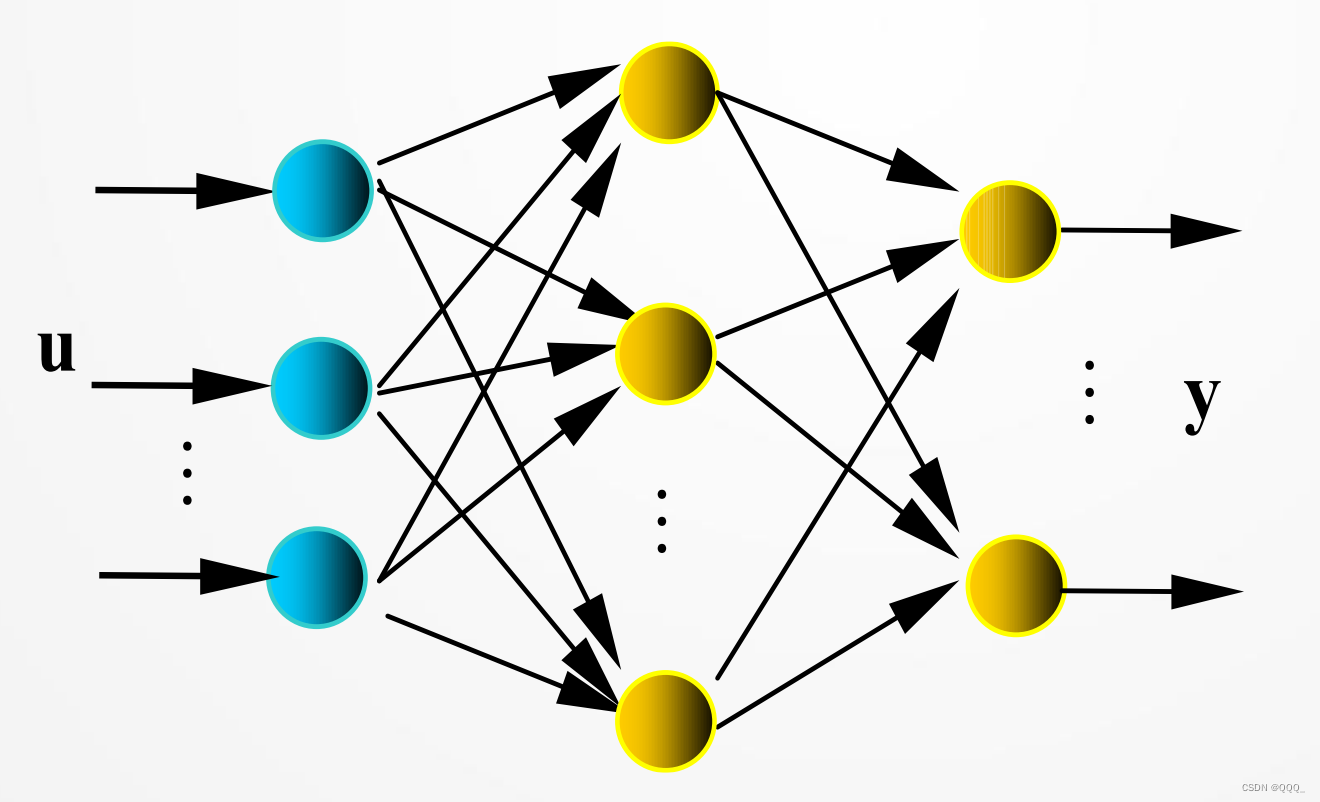
BP网络

多层前馈网络的反向传播（BP）学习算法，简称BP算法，是有导师的学习，它是梯度下降法在多层前馈网中的应用。
网络结构：见图，𝐮（或𝐱 ）、𝐲是网络的输入、输出向量，神经元用节点表示，网络由输入层、隐层和输出层节点组成，隐层可一层
，也可多层（图中是单隐层），前层至后层节点通过权联接。由于用BP学习算法，所以常称BP神经网络。