比赛链接

官方讲解（不分P不分段直接两小时怼上来是坏文明 ）

这场的题很棒，思维有难度，考察的知识点广泛，有深度，很透彻。感觉学到了很多。建议补题。

---

A 小红的正整数自增

思路：

签到。

可以模拟一下，看加上几次，个位就变成 $0$ 了。

或者可以用 $10$ 减一下个位数，看看离进位差几。

code：

#include <cstdio>
#include <iostream>
using namespace std;int n;int main(){cin>>n;cout<<(10-n%10)%10;return 0;
}

---

B 小红的抛弃后缀

思路：

有一个初等数论的知识点可以秒掉此题：$$一个数是9的倍数\iff 这个数十进制数码的和能被9整除$$

比如 $1233$ 的各个数位上的数分别为 $1,2,3,3$，它们的和 $1+2+3+3=9$ 可以被 $9$ 整除，那么 $1233$ 这个数就可以被 $9$ 整除，反之也成立。

所以我们删掉一个后缀使得剩余的数能被 $9$ 整除，其实就相当于去验证剩余的前缀的数字之和能被 $9$ 整除即可。

我们跑一遍前缀和，并检查每个前缀和能否被 $9$ 整除。能被整除的前缀和的个数就是答案。

code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
const int maxn=1e5+5;int n,s[maxn],ans;
string str;int main(){cin>>str;n=str.length();str=" "+str;for(int i=1;i<=n;i++){s[i]=(s[i-1]+str[i]-'0')%9;if(!s[i])ans++;}cout<<ans<<endl;return 0;
}

不止 $9$ 有这种性质，其他很多数也有各种不同的性质。它们基本都是通过同余的性质来证明的，证明可以看：初等数论-同余性质的应用。

---

C 小红的字符串构造

思路：

如果我们全部填入一个相同的字母，那么最多可以出现 $1+2+3+\cdots +n-1=\frac{n\ast (n-1)}{2}$ 个回文串，但是题目却保证 $k\le \frac{n}{2}$，这就很奇怪。

考虑到我们两个相同的字母放在一起就可以用两个字符组成一个回文串，这就正好和题目的 $k\le \frac{n}{2}$ 对应上了。所以我们用 $aabbccaabbcc\dots$ 这种方式来组回文串——两个字符组成一个回文串，为了防止出现其他回文串，需要至少三种字符来进行循环。

$k$ 个回文串，那么前面需要 $2k$ 个字符来凑。后面多余的位置就可以用 $defdefdef\dots$ 这种方式来填充，同样的为了防止出现回文串，需要至少三种字符进行循环。

code：

"abc"[i%3] 相当于

char str[]="abc";str[i%3];

前面的字符串相当于一个匿名的字符数组。并且占有空间（应该？）。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int n,k;
string s;int main(){cin>>n>>k;for(int i=1;i<=k;i++){s+="abc"[i%3];s+="abc"[i%3];}for(int i=2*k+1;i<=n;i++)s+="def"[i%3];cout<<s<<endl;return 0;
}

---

D 小红的平滑值插值

思路：

发现如果相邻两项的差值超过了 $k$，我们就需要向中间插入数字，将这个差值降下来。

而降差值的时候可以贪心地来进行，即每差 $k$ 才插一个，差值要是还大就继续插，够了就往下看。这样如果差值为 $d$ 的话，我们需要插 $\lceil \frac{d}{k}\rceil -1=\lfloor \frac{d-1}{k}\rfloor$个数。

不过如果中间不存在一个差值大于等于 $k$ 的位置的话，我们就需要人为造一个差值为 $k$ 的相邻的数。比如在最后补一个数，使得它和前面那个数差值为 $k$。所以我们需要看一下中间有没有一个差值大于等于 $k$ 的位置。

code：

#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e5+5;int n,k,a[maxn];
long long cnt=0;int main(){cin>>n>>k;for(int i=1;i<=n;i++)cin>>a[i];bool flag=false;for(int i=1,d;i<n;i++){d=abs(a[i]-a[i+1]);if(d>=k){cnt+=(d-1)/k;flag=true;}}if(!flag)cnt++;cout<<cnt<<endl;return 0;
}

---

E 小苯的等比数列

思路：

没想到被一个 $1799$ rate 的比赛的 $E$ 题单防了。

这个题的思路其实很简单：就是枚举每一个数，让它作为等比数列的首项，并枚举公比，暴力进行验证即可。

当然需要一点点优化，因为每个数的值域很小，所以我们直接可以把每个数桶排序一下，把它扔进桶里，这样查找一个数的时间复杂度就可以降为 $O(1)$ 的。不过公比为 $1$ 的情况会不停验证下去，所以需要特判解决，我们之前用桶可以直接记录每个数的个数，就可以解决掉公比为 $1$ 的情况。这时候再暴力就可以做到接近 $O(n\ast logn)$ 的逆天时间复杂度。

为啥时间复杂度这么低？枚举每个数当然是 $O(n)$ 的，而对每个公比 $d$，我们最多只需要验证到 $\frac{n}{d}$ 个公比就可以直接返回了（因为后面的数，数列第二项就会直接超出 $2\ast 10^5$），而每个公比只需要验证 $lo{g}_d(2\ast 10^5)$ 次就会超出 $2\ast 10^5$ 的值域范围。可以写个程序打个表：（第一行是公比 $d$，第二行是执行次数 $lo{g}_d(2\ast 10^5)$）

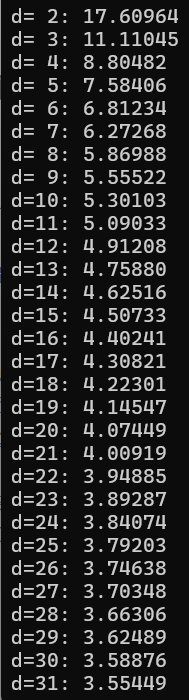
其实平均每个公比也就跑了 2.00278 次。所以总的时间复杂度大概就是 $O(\frac{n}{2}+\frac{n}{3}+\cdots +\frac{n}{n}\approx n\ast logn)$，然后带上一点常数，所以这样暴力跑是不会超时的。逆天。

code：

#include <iostream>
#include <cstdio> 
#include <vector>
#include <set>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;int n,vis[maxn],ans;int main(){cin>>n;for(int i=1,t;i<=n;i++){cin>>t;vis[t]++;}for(ll a0=1;a0<=2e5;a0++){if(!vis[a0])continue;ans=max(ans,vis[a0]);for(ll d=2;d<=2e5;d++){if(a0*d>2e5)break;int cnt=1;for(ll a=a0*d;;a*=d){if(a>2e5 || !vis[a]){ans=max(ans,cnt);break;}else cnt++;}}}cout<<ans<<endl;return 0;
}

---

F 小苯的回文询问

思路1（莫队）：

发现是离线的区间询问，可以尝试使用莫队！借鉴这位大佬的。

考虑到是子序列是长度 $>2$ 的回文串。所以我们只要保证有 有两个相同的数中间隔了一些数 这种情况出现就行。但是想用莫队就需要通过一些参数来描述上面这种情况，并且 $[l,r]$ 区间的参数可以 $O(1)$ 拓展到相邻的 $[l-1,r],[l+1,r],[l,r-1],[l,r+1]$ 区间。

两个相同的数中间隔了一些数的话，相当于需要两个相同的数不相邻，或者有三个及以上的相同的数。所以我们用 $f1$ 变量记录三个及以上的相同的数的个数，用 $f2$ 变量记录两个相同的数的个数。

如果 $f1>0$ 那么一定是有回文串的。如果 $f1==0$，这时候我们需要保证 两个相同的数 至少有一对不相邻，所以我们可以设置一个变量 $sum$，记录相邻的相同的数有几对，如果 $f2!=sum$，就说明至少有一对相同的数不相邻，这时也有回文串。

不过每个数的值域太大了，如果使用 $map$，时间会多出一个 $log$，总的时间复杂度为 $O(n\ast logn+q\sqrt{n}\ast logn)$，会超时。所以我们对每个数离散化预处理一下，这样时间复杂度就变成了 $O(n\ast logn+q\sqrt{n})$，可以通过。

code1：

上面那个大佬写的更加优美。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
using namespace std;
const int maxn=1e5+5;int n,q;int len,tot;
int a[maxn],L[maxn],R[maxn],belong[maxn];void init(){len=log2(n);tot=(n+len-1)/len;for(int i=1;i<=tot;i++){L[i]=R[i-1]+1;R[i]=i*len;}R[tot]=n;for(int i=1;i<=tot;i++)for(int j=L[i];j<=R[i];j++)belong[j]=i;
}struct itv{int l,r,id;bool ans;
}qy[maxn<<1];bool cmp1(const itv a,const itv b){return (belong[a.l]^belong[b.l])?a.l<b.l:((belong[a.l]&1)?a.r<b.r:a.r>b.r);}
bool cmp2(const itv a,const itv b){return a.id<b.id;}int f1,f2,sum;
//map<int,int> mp;
int mp[maxn];
void add(int x){mp[x]++;if(mp[x]==2)f1++;else if(mp[x]==3)f2++;
}
void del(int x){if(mp[x]==2)f1--;else if(mp[x]==3)f2--;mp[x]--;
}vector<int> ttt;
int find(int x){return lower_bound(ttt.begin(),ttt.end(),x)-ttt.begin()+1;
}int main(){cin>>n>>q;init();for(int i=1;i<=n;i++)cin>>a[i],ttt.push_back(a[i]);sort(ttt.begin(),ttt.end());ttt.erase(unique(ttt.begin(),ttt.end()),ttt.end());for(int i=1;i<=n;i++)a[i]=find(a[i]);
//	for(int i=1;i<=n;i++)cout<<a[i]<<" \n"[i==n];for(int i=1;i<=q;i++)cin>>qy[i].l>>qy[i].r,qy[i].id=i;sort(qy+1,qy+q+1,cmp1);int tl=1,tr=0,cnt=0;for(int i=1,l,r,t;i<=q;i++){l=qy[i].l;r=qy[i].r;while(tr<r){add(a[++tr]);if(a[tr]==a[tr-1])sum++;}while(tr>r){if(a[tr]==a[tr-1])sum--;del(a[tr--]);}while(tl<l){if(a[tl]==a[tl+1])sum--;del(a[tl++]);}while(tl>l){add(a[--tl]);if(a[tl]==a[tl+1])sum++;}if(f2 || (f1 && sum!=f1))qy[i].ans=true;}sort(qy+1,qy+q+1,cmp2);for(int i=1;i<=q;i++)puts((qy[i].ans)?"YES":"NO");return 0;
}

思路2：

同样的，我们想要两个相同的数中间隔了一些数的话，这时就是有回文子序列的。那么我们可以处理出每个位置的数的前一个不相邻的相同数的位置，假设是 $lst[i]$。这样，对一个区间，我们只要保证 $[l,r]$ 区间里有一个 $lst[i]\ge l$ 即可。

因为只要存在一个这样的 $lst[i]$ 就行，所以我们查询 $lst$ 的区间最大值，只要这个最大值满足条件就行了。而区间离线询问，可以跑线段树，ST表啊之类的都可以。

不过发现一个性质，就是 $lst[i]<i$。所以在 $i<l$ 的位置，都满足 $lst[i]<l$，这意味着 $lst[i]>l$ 的情况一定发生在 $i\in [l,r]$ 的区间内，查询最大值的时候加入前缀不会影响结果大于等于l。因此我们直接处理出 $lst$ 的前缀 $max$，然后查询是否满足 $lst[r]\ge l$ 就行了。

code2：

#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
const int maxn=1e5+5;int n,q;
int a[maxn],lst[maxn];
map<int,int> mp;int main(){cin>>n>>q;for(int i=1;i<=n;i++){cin>>a[i];lst[i]=mp[a[i]];mp[a[i]]=i;}for(int i=n;i>=1;i--)if(lst[i]==i-1)lst[i]=lst[lst[i]];for(int i=2;i<=n;i++)lst[i]=max(lst[i-1],lst[i]);for(int i=1,l,r;i<=q;i++){cin>>l>>r;puts((lst[r]>=l)?"YES":"NO");}return 0;
}

---

G 小红的区间删除

思路：

区间删除很难想，不如先看看单点删除。一个数放在某个位置上可以产生多少逆序对，就说明被删掉后会失去多少逆序对。而在某个位置插入一个数的话，它会和这个位置之前的每个比它大的数产生一对逆序对，以及和这个位置之后的每个比它小的数产生一对逆序对。

因此我们删掉一个点的剩余逆序对对数，相当于总的逆序对个数要减去 序列中在这个位置之前的比它大的数的个数和这个位置之后的比它小的数的个数。而区间删除就是一个点一个点地删掉。

我们要删掉中间一段连续的区间，然后剩余的部分的逆序对个数 $\ge k$，所以我们可以通过上面的单点修改一个一个删掉中间的部分，得到剩余部分的逆序对个数。

因为我们删掉的数越多，逆序对数就越少，它是单调的。所以我们只要对每个右端点 $r$ 找到满足条件的最小的 $l$，那么中间所有的位置都可以作为满足条件的左端点。而也因为是单调的，我们可以使用双指针来移动左右端点。这样移动指针的复杂度就降为了 $O(n)$，移动一次的复杂度为 $O(logn)$，可以通过。

不过因为什么都不删也是一种方法，所以我们需要特判一下，如果什么都不删都不满足条件，就直接输出 $0$。否则答案额外加上这个特殊情况。

值域给的很贴心，不用离散化了。

code：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const int maxf=1e6+5;int n;
ll k;
int a[maxn];ll cnt=0,ans;//剩余部分逆序对个数 答案 
struct tree_array{const int _n=1e6;int tr[maxf];int lowbit(int x){return x&-x;}void add(int idx,int x){for(int i=idx;i<=_n;i+=lowbit(i))tr[i]+=x;}int query(int idx){int ans=0;for(int i=idx;i;i-=lowbit(i))ans+=tr[i];return ans;}int qpre(int idx){//<idx的数个数 return query(idx-1);}int qsuf(int idx){//>idx的数个数 return query(_n)-query(idx);}
}t1,t2;int main(){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];cnt+=t2.qsuf(a[i]);t2.add(a[i],1);}if(cnt>=k)ans=1;else return cout<<0,0;for(int l=1,r=1;r<=n;r++){//删掉a[r] cnt-=t1.qsuf(a[r])+t2.qpre(a[r]);t2.add(a[r],-1);//加入a[l] while(l<=r && cnt<k){cnt+=t1.qsuf(a[l])+t2.qpre(a[l]);t1.add(a[l],1);l++;}ans+=(r-l+1);}cout<<ans<<endl;return 0;
}