目录

描述

输入

输出

样例输入 

样例输出 

思路

建树 

第一次错误解法（正确解法在下面，可跳过这一步）

正确解法

code 

---

描述

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

输入

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

输出

You need to answer all Q commands in order. One answer in a line.

样例输入 

10 5
C 3 6 3
Q 2 4

样例输出 

9
15

思路

不要看这题全英文，但这题就是属于线段树模版题，基本做法是一样的

建树 

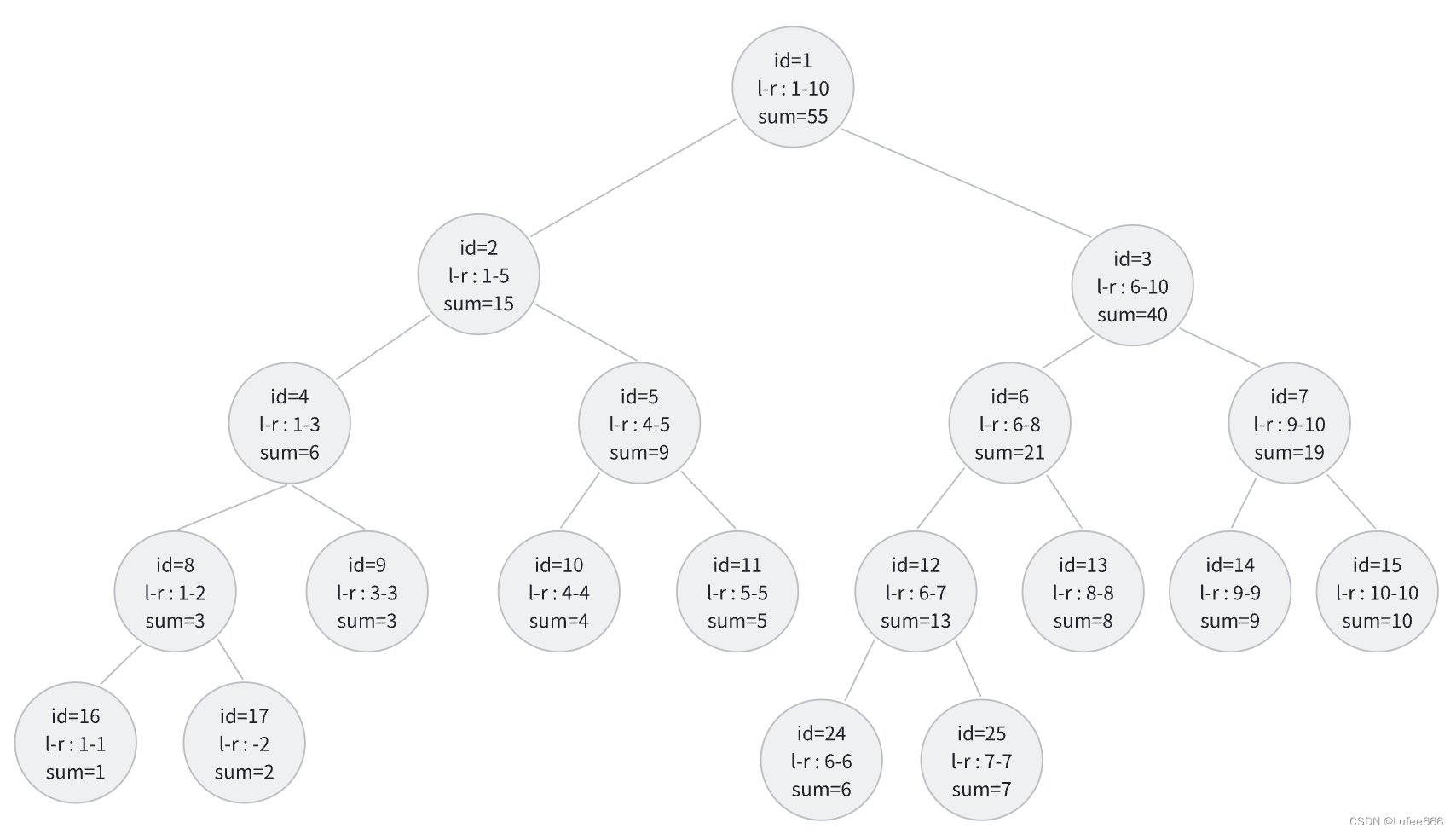
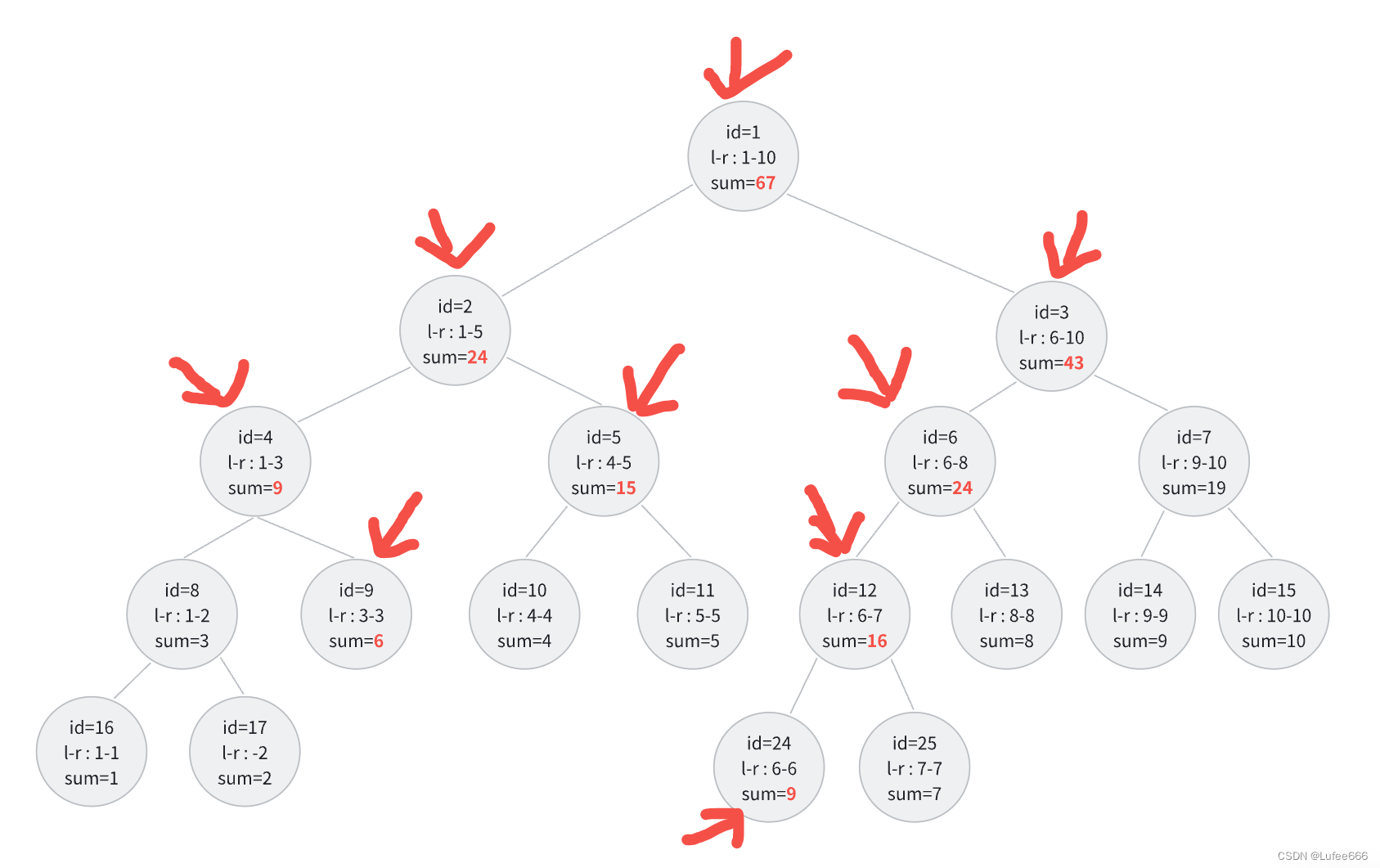
第一次错误解法（正确解法在下面，可跳过这一步）

树没有更新成功，id=10，id=11理论上是要继续更新他们的sum值，但我的错误代码没有更新

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
const int N = 100010;
#define ll long long
ll nums[N];
struct Tree {int l, r;ll sum;ll tag;
}tree[N << 2];
void pushup(int u) {tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
}
void build(int l, int r, int u) {if (l == r) tree[u] = { l,r,nums[l] };//要与结构体Tree一一对应 else {tree[u] = { l,r };int mid = (l + r) >> 1;build(l, mid, u << 1);build(mid + 1, r, u << 1 | 1);pushup(u);}
}
ll query(int L, int R, int u) {int l = tree[u].l, r = tree[u].r;if (l >= L && r <= R)return tree[u].sum;int mid = (l + r) >> 1;ll sum = 0;if (L <= mid) sum += query(L, R, u << 1);if (R > mid) sum += query(L, R, u << 1 | 1);return sum;
}
void pushdown(int u, int ln, int rn) {if (tree[u].tag) {tree[u << 1].tag += tree[u].tag;tree[u << 1 | 1].tag += tree[u].tag;tree[u << 1].sum += tree[u].tag * ln;tree[u << 1 | 1].sum += tree[u].tag * rn;tree[u].tag = 0;}
}
void updatespan(int L, int R, int value, int u) {int l = tree[u].l, r = tree[u].r;int mid = (l + r) >> 1;if (l >= L && r <= R) {tree[u].tag += value;tree[u].sum += value * (r - l + 1);return;}pushdown(u, mid - l + 1, r - mid);if (L <= mid) updatespan(L, R, value, u << 1);if (R > mid) updatespan(L, R, value, u << 1 | 1);pushup(u);
}
int main()
{int n, q;while (scanf("%d%d", &n, &q) != EOF) {for (int i = 1; i <= n; i++) scanf("%lld", &nums[i]);build(1, n, 1);while (q--) {string cz;int op1, op2;cin >> cz;if (cz == "C") {int val;scanf("%d%d%d", &op1, &op2, &val);updatespan(op1, op2, val, 1);}else {scanf("%d%d", &op1, &op2);printf("%lld\n", query(op1, op2, 1));}}}return 0;
}

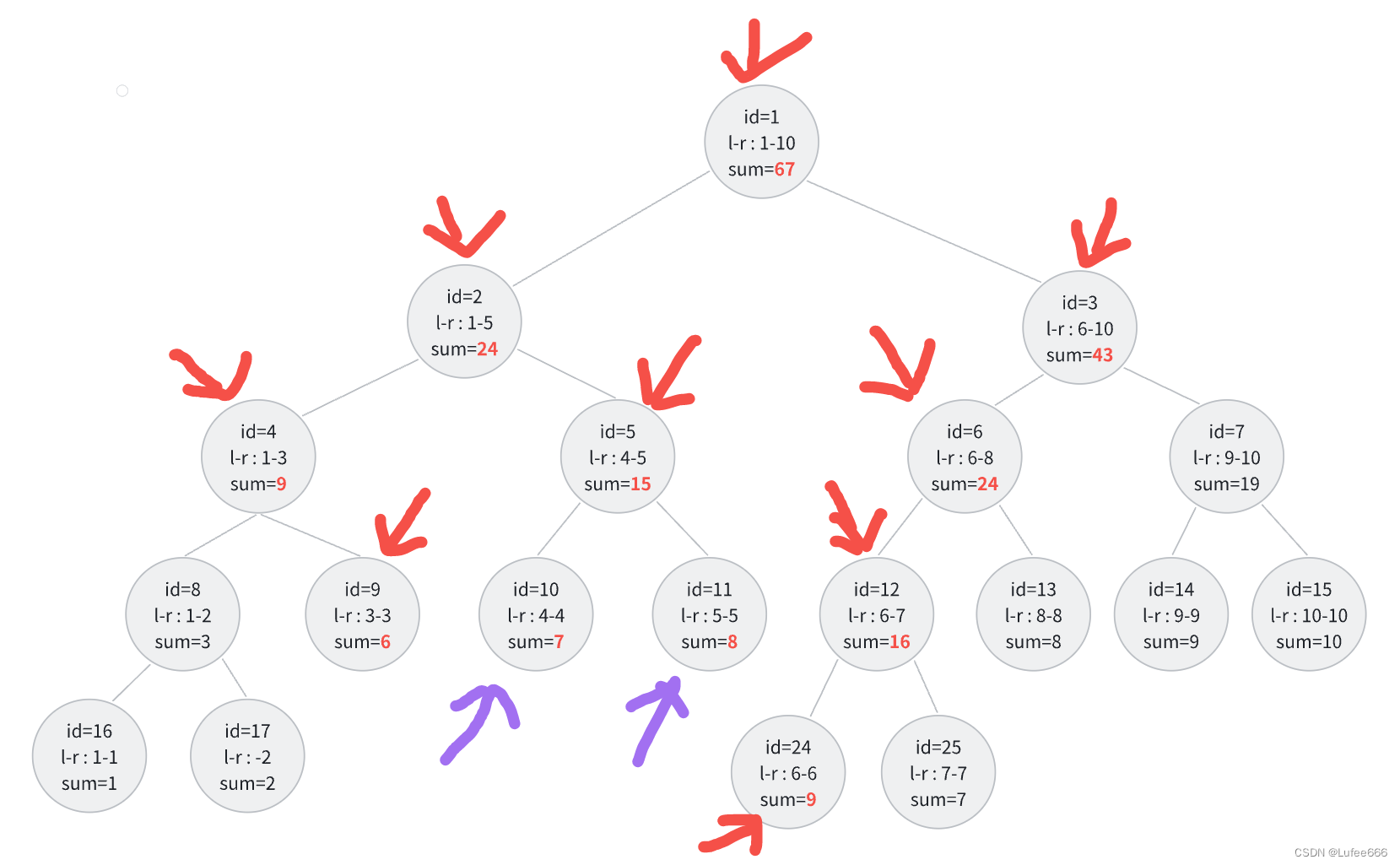
正确解法

关键在于updatespan函数中，if语句中我没有继续pushdown导致错误

  

code 

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
using namespace std;
const int N = 100010;
#define ll long long
ll nums[N];
struct Tree {int l, r;ll sum;ll tag;
}tree[N << 2];
void pushup(int u) {tree[u].sum = tree[u << 1].sum + tree[u << 1 | 1].sum;
}
void build(int l, int r, int u) {if (l == r) {tree[u] = { l,r,nums[l] };//要与结构体Tree一一对应 else {tree[u] = { l,r };int mid = (l + r) >> 1;build(l, mid, u << 1);build(mid + 1, r, u << 1 | 1);pushup(u);}
}
ll query(int L, int R, int u) {int l = tree[u].l, r = tree[u].r;if (l >= L && r <= R)return tree[u].sum;int mid = (l + r) >> 1;ll sum = 0;if (L <= mid) sum += query(L, R, u << 1);if (R > mid) sum += query(L, R, u << 1 | 1);return sum;
}
void pushdown(int u, int ln, int rn) {if (tree[u].tag) {tree[u << 1].tag += tree[u].tag;tree[u << 1 | 1].tag += tree[u].tag;tree[u << 1].sum += tree[u].tag * ln;tree[u << 1 | 1].sum += tree[u].tag * rn;tree[u].tag = 0;}
}
void updatespan(int L, int R, int value, int u) {int l = tree[u].l, r = tree[u].r;int mid = (l + r) >> 1;if (l >= L && r <= R) {tree[u].tag += value;tree[u].sum += value * (r - l + 1);pushdown(u, mid - l + 1, r - mid);//关键return;}pushdown(u, mid - l + 1, r - mid);if (L <= mid) updatespan(L, R, value, u << 1);if (R > mid) updatespan(L, R, value, u << 1 | 1);pushup(u);
}
int main()
{int n, q;while (scanf("%d%d", &n, &q) != EOF) {for (int i = 1; i <= n; i++) scanf("%lld", &nums[i]);build(1, n, 1);while (q--) {string cz;int op1, op2;cin >> cz;if (cz == "C") {int val;scanf("%d%d%d", &op1, &op2, &val);updatespan(op1, op2, val, 1);}else {scanf("%d%d", &op1, &op2);printf("%lld\n", query(op1, op2, 1));}}}return 0;
}