图论-最短路

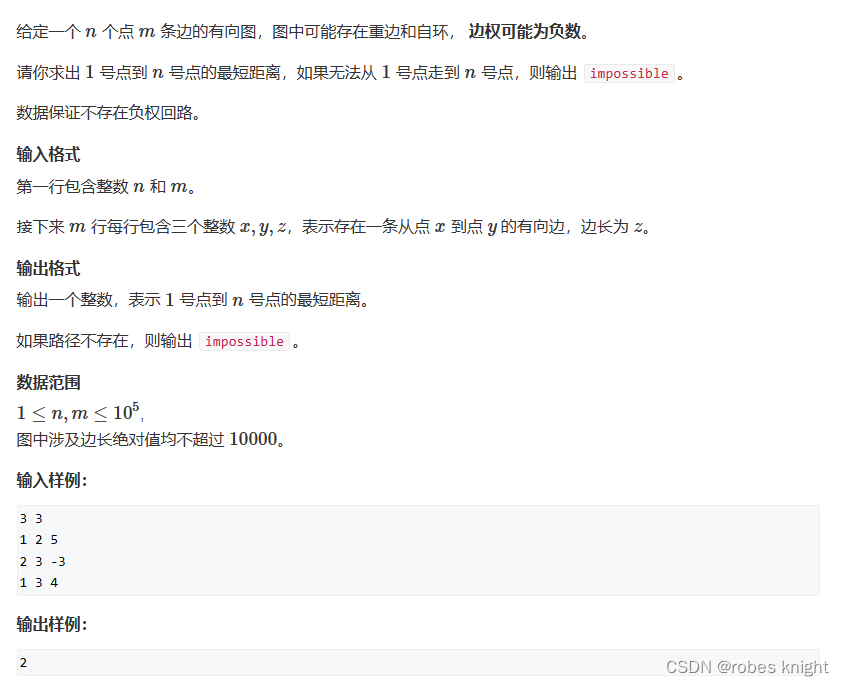
一、不存在负权边-dijkstra算法

dijkstra算法适用于这样一类问题：

从起点 start 到所有其他节点的最短路径。

其实求解最短路径最暴力的方法就是使用bfs广搜一下，但是要一次求得所有点的最短距离我们不可能循环n次，这样复杂度太高，因此dijlstra算法应运而生，算法流程如下：

（待补充）

对于：

稠密图一般使用邻接矩阵+朴素dji

稀疏图使用邻接表+堆优化dji

1.1 朴素djikstra算法

算法模板：

#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;const int N = 510;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstra(){memset(st,0,sizeof(st));memset(dist,0x3f,sizeof(dist));dist[1] = 0;//对于每个点都要遍历所有点，也即是穷举for(int i = 0;i < n; i++){int t = -1;//临时存储第i次处理的点//一、遍历所有点，在所有没有访问过的点中找到距离最近的点for(int j = 1; j<= n;j++)if(!st[j] && (t == -1 || dist[t] > dist[j])){t = j;}//st[t] = true;//二、用1-t的路径长度 + t - j的边长度来更新dist[j];for(int j = 1;j <= n;j++){dist[j] = min(dist[j],dist[t] + g[t][j]);}}if(dist[n] == 0x3f3f3f3f)return -1;return dist[n];}

1.2 优先级队列优化的djikstra

首先我们分析，如果是稀疏图，什么导致的朴素版djikstra复杂度高，首先我们用的是邻接表来存图，那么就要用bfs相应的方法进行遍历，那么我们需要先while处理点再内层处理边，如果不优化，复杂度依旧是o(mn)

这是因为我们将所有的顶点都遍历了，用于寻找最小距离点，如果我们使用堆来优化（而不是一般bfs中的普通队列），每次使用优先级队列来存放顶点，因为理想情况下优先级队列中最多装 n 个节点，对优先级队列的操作次数和 m 成正比，所以整体的时间复杂度就是 O(mlogn)。

红字解释：

因为在修改其它顶点最短距离的过程中，堆优化版本并没有遍历所有的顶点，而是遍历所有与当前选取的最小顶点有关的边，从一小部分顶点出发就能到达所有顶点，因此没有必要遍历所有顶点

优先级队列解释：

priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;

pair中第一个整数可以表示从源点到该顶点的距离，第二个整数表示顶点的编号。

vector<pair<int, int>>指定了底层容器类型。

greater<>：默认小顶堆，less<>:大顶堆排序

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
//只存一个点，因为另一个点是邻接表的表头
struct Edge {int to, weight;
};vector<Edge> adj[N];
int dist[N];
bool visited[N];void dijkstra(int source) {memset(dist, 0x3f, sizeof(dist));memset(visited, 0, sizeof(visited));priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;dist[source] = 0;pq.push({0, source});while (!pq.empty()) {int u = pq.top().second;pq.pop();if (visited[u]) continue;visited[u] = true;for (auto &e : adj[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;pq.push({dist[v], v});}}}
}int main() {int n, m;cin >> n >> m;for (int i = 0; i < m; ++i) {int x, y, z;cin >> x >> y >> z;adj[x].push_back({y, z});}dijkstra(1); // 假设你想要从节点 1 找到到其他所有节点的最短路径if (dist[n] == INF) cout << "-1\n"; // 检查是否存在从1到n的路径else cout << dist[n] << "\n";return 0;
}

二、存在负权值 -bellma-ford算法

1.朴素Bellman-Ford算法

三角不等式：

对于所有点都有：

dist[b] <= dist[a] + w

松弛操作：

dist[b] = min(dist[b], dist[a] + w)

注意：如果一个图中存在负权回路，那么可能不存在最短路

#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;
const int N = 510;
const int M = 10010;
int n,m,k;
int dist[N],backup[N];
// 边，a表示出点，b表示入点，w表示边的权重
struct edge{int from;int to;int weight;
}edges[M];void bellman_ford(){memset(dist,0x3f,sizeof dist);dist[1] =0;
// 如果第n次迭代仍然会松弛三角不等式（存在更新），就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。for(int i = 0;i < k;i++){
// 备份，防止读后写memcpy(backup,dist,sizeof(dist));for(int j = 0;j < m; j++){int from = edges[j].from;int to  = edges[j].to;int weight = edges[j].weight;dist[to] = min(dist[to],backup[from] + weight);}}}int main(){scanf("%d%d%d",&n,&m,&k);for(int i = 0;i < m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);edges[i] = {a,b,c};}bellman_ford();if(dist[n] > 0x3f3f3f3f/2){puts("impossible");}else{printf("%d\n",dist[n]);}return 0;
}

除了可以用邻接矩阵和邻接表外，还可用三元组存储图
允许存在负权边，而Dijkstra算法不允许
外循环次数决定最小路径的最大边数
若第n次迭代有修改，根据容斥原理知道，一定存在负权环（整个环的权重和为负数）
实际应用：换乘不超过k次的最短路径（限制路径的边数）
backup用于保存上次迭代的结果，避免“写后读”。Dijkstra算法不存在这种情况
由于存在负权回路（注意不是负权边），因此负权回路有可能把自定义的无穷大0x7f7f7f7f变小，由于最多修改10000×10000=108，10000×10000=108，而0x7f7f7f7f>2×108>2×108，故0x7f7f7f7f / 2依旧是“无穷大”，故可用dist[n] > 0x7f7f7f7f / 2判断是否是无穷大
时间复杂度为O(mn)

2.普通队列优化的bellman-ford算法

#include<cstring>
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
//只存一个点，因为另一个点是邻接表的表头
struct Edge {int to, weight;
};vector<Edge> adj[N];
int dist[N];
bool used[N];
int n, m,k;void spfa(int source) {memset(dist, 0x3f, sizeof(dist));dist[source] = 0;queue<int> pq;pq.push(source);used[source] = true;while (!pq.empty()) {int u = pq.front();pq.pop();used[u] = false;for (auto &e : adj[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;if(!used[v]){pq.push(v);used[v] = true;}}}}
}int main() {cin >> n >> m ;for (int i = 0; i < m; ++i) {int x, y, z;cin >> x >> y >> z;adj[x].push_back({y, z});}spfa(1);if(dist[n] > 0x3f3f3f3f/2){puts("impossible");}else{printf("%d\n",dist[n]);}return 0;
}

时间复杂度：

最好：o(m)

最差：o（mn）

spfa相较于djikstra,如果题目中不进行针对性限制，一般是会比djikstra更快的

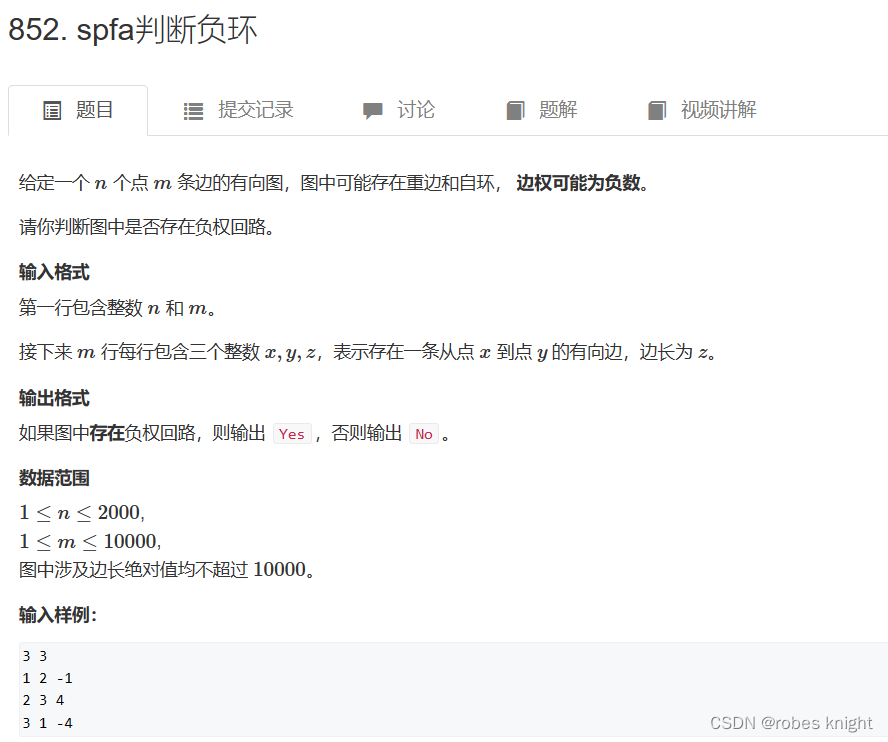
spfa求负环数量：

#include<cstring>
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
//只存一个点，因为另一个点是邻接表的表头
struct Edge {int to, weight;
};vector<Edge> adj[N];
int dist[N],cnt[N];
bool used[N];
int n, m,k;
bool iscir = false;void spfa(int source) {// memset(dist, 0x3f, sizeof(dist));queue<int> pq;for(int i =1;i <= n;i++){// dist[i] = 0;pq.push(i);used[i] = true;}while (!pq.empty()) {int u = pq.front();pq.pop();used[u] = false;for (auto &e : adj[u]) {int v = e.to;int w = e.weight;if (dist[v] > dist[u] + w) {dist[v] = dist[u] + w;//判断是否存在负权值cnt[v] = cnt[u] + 1;if(cnt[v] >= n) {iscir = true;return;}if(!used[v]){pq.push(v);used[v] = true;}}}}
}int main() {cin >> n >> m ;for (int i = 0; i < m; ++i) {int x, y, z;cin >> x >> y >> z;adj[x].push_back({y, z});}spfa(1);if(iscir){printf("Yes");}else{printf("No");}return 0;
}

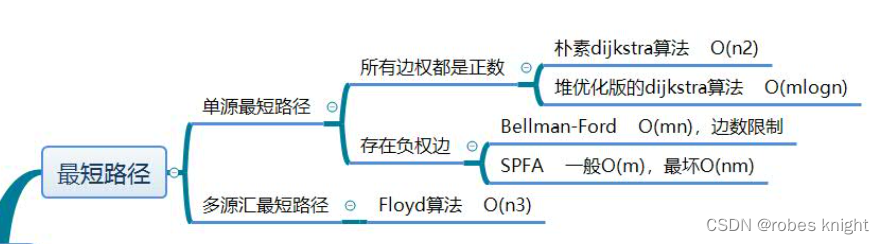
三、Floyd算法

const int INF = 1E9;
// 初始化：for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )if (i == j) d[i][j] = 0;else d[i][j] = INF;// 算法结束后，d[a][b]表示a到b的最短距离
void floyd()
{for (int k = 1; k <= n; k ++ )for (int i = 1; i <= n; i ++ )for (int j = 1; j <= n; j ++ )d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}