CaT论文翻译

CaT: Balanced Continual Graph Learning with Graph Condensation

CaT：通过图压缩实现平衡的连续图学习

Abstract

持续图学习(CGL)的目的是通过以流方式输入图数据来持续更新图模型。由于模型在使用新数据进行训练时很容易忘记以前学到的知识，因此灾难性遗忘问题一直是 CGL 的主要关注点。最近的基于重放的方法旨在通过使用(1)整个新出现的数据和(2)基于采样的内存库来更新模型来解决这个问题，该内存库存储重放的图以近似历史数据的分布。更新模型后，从传入图形中采样的新重放图形将被添加到现有的内存库中。尽管这些方法对于 CGL 来说直观且有效，但本文还是指出了两个问题。首先，当存储预算紧张时，大多数基于采样的方法都难以完全捕获历史分布。其次，复杂的新图数据规模和轻量级存储库存在显着的数据不平衡，导致训练不平衡。为了解决这些问题，本文提出了压缩和训练(CaT)框架。在每次模型更新之前，新出现的图都会压缩为一个小而信息丰富的合成重放图，然后将其与历史重放图一起存储在压缩图形存储器中。在持续学习阶段，使用内存训练方案直接使用压缩图内存而不是整个新出现的图来更新模型，从而缓解了数据不平衡问题。在四个基准数据集上进行的广泛实验成功地证明了所提出的 CaT 框架在有效性和效率方面的卓越性能。该代码已发布在 https://github.com/superallen13/CaT-CGL上。

I. INTRODUCTION

与传统的图表示学习将图作为静态数据并将数据作为整体训练模型相比，连续图学习(CGL)处理更实际的场景，其中图数据不断出现并以流式方式馈送到模型中。

对于CGL问题，最大的挑战是解决灾难性的遗忘问题，即模型容易忘记从历史图数据中学习的知识，同时过分强调传入的数据。由于存储和计算方面的硬件限制，当在训练期间访问整个历史图不切实际时，CGL模型会发生灾难性遗忘问题。如果直接使用传统的图神经网络(GNN)来不断从传入的图中学习，则由于历史和当前图之间的分布偏移，来自历史分布的数据的模型性能往往会恶化。最近，已经进行了一些尝试来解决这个灾难性的遗忘问题，利用正则化惩罚，架构重新设计和重播图。作为三种方法中的佼佼者，基于重放的CGL模型通过采样方法将重放的图存储在记忆库中，以保持历史分布，解决灾难性遗忘问题，从而提高了性能和可塑性。例如，ER-GNN将来自历史图形的信息节点存储在内存库中，而SSM将传入的图形稀疏化为重播的图形。

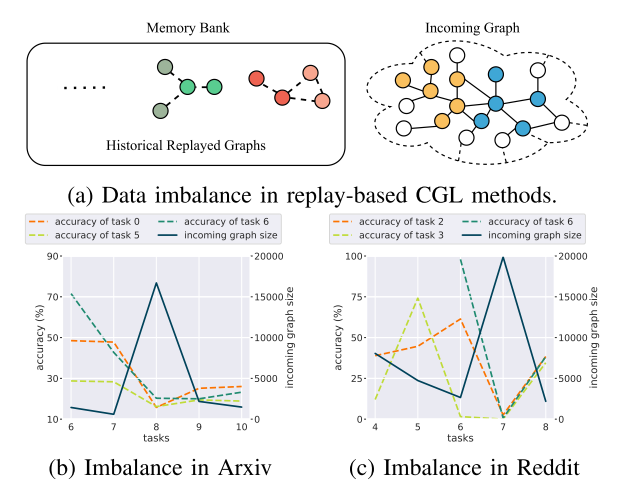
图1：基于重放的CGL方法中的不平衡学习问题。(a)在基于重放的方法的更新阶段中，存储库中的重放图和传入图都用于训练。通常，重放的图形明显小于传入的图形。在(B)和©中，显示了CGL模型在Arxiv和Reddit数据集上的预测精度。当传入图的大小比重播图的大小大得多时，例如Arxiv中的任务8和Reddit中的任务7，从先前任务中提取的数据的模型性能将急剧下降。这是由于持续学习中的数据不平衡问题。

尽管基于重放的方法直观且有效，但在我们研究这些方法的过程中观察到两个主要问题。首先，现有的基于回放的CGL方法通常需要较大的空间来存储尽可能多的历史信息，以获得具有竞争力的性能。当存储预算有限时，这些存储体很难呈现历史数据分布的全貌。其次，很难在传入和重放的图上平衡模型更新训练，因为传入的图通常在规模上比重放的图大得多。图1(a)展示了不平衡学习的情况，其中传入的图明显大于重放的图。图1(B)和图1©显示，当传入的图明显大于重放的图时，历史数据上的模型性能下降。

鉴于上述讨论，我们有理由设计一种新颖的框架，该框架可以同时提高记忆库的有效性和效率，并平衡基于重放的 GCL 方法的持续训练。为了生成小但信息丰富的重放图，最近的图压缩技术已经表现出巨大的潜力，它可以使用可微分方法将图压缩为更小的合成图。与基于采样的重放图相比，图压缩具有在不影响性能的情况下生成更小且可学习的重放图的优点。对于不平衡训练，由于数据规模不平衡的性质，当直接将回放图和整个传入图结合起来训练模型时，很难保持平衡。相反，如果从压缩方法导出的合成重放图能够在不牺牲性能的情况下支持模型训练，则可以绕过使用整个传入图进行模型更新，而纯粹依赖合成图。已经表现出巨大的潜力，可以使用可微分的方法将图压缩成更小的合成图。与基于采样的重放图相比，图压缩具有在不影响性能的情况下生成更小且可学习的重放图的优点。对于不平衡训练，由于数据规模不平衡的性质，当直接将回放图和整个传入图结合起来训练模型时，很难保持平衡。相反，如果从压缩方法导出的合成重放图能够在不牺牲性能的情况下支持模型训练，则可以绕过使用整个传入图进行模型更新，而纯粹依赖合成图。为了实现这两个目标，我们为 CGL 提出了一个基于重放的压缩和训练 (CaT) 框架。在持续学习过程中，它维护一个小而有效的压缩图存储器(CGM)，该存储器随着模型更新之前从输入图压缩的合成重放图进行扩展。在模型更新阶段，所提出的框架使用的训练策略是内存训练(TiM)，其中模型仅使用内存库进行更新。 TiM 确保压缩合成图具有与重放图相似的大小，从而缓解不平衡问题。贡献如下：

对于CGL问题，提出了一种新颖的框架CaT，其中包含CGM模块以减少重放图的大小和TiM方案以平衡连续训练。
CGM 是通过使用分布匹配对大型传入图执行图压缩而得出的。
TiM 的开发是为了平衡使用大输入图和小内存库的训练。
在四个基准数据集上进行的大量实验验证了CaT 的最先进性能。

II. RELATED WORK

A. Graph Neural Networks 图神经网络

图神经网络(GNNs)是基于图的任务的有效工具。 GCN采用拉普拉斯归一化进行消息传播。 GAT被提议使用注意力机制进行消息传递。SGC通过去除非线性激活层来简化GCN。GraphSAGE使用节点采样来处理大规模图表示学习。

B. Graph Continual Learning 图持续学习

图持续学习是处理流图数据的任务。计算机视觉领域对持续学习进行了研究。在图领域，CGL方法可以分为三个分支：正则化、重播和基于架构的方法。TWP通过添加正则化来保留历史图的拓扑信息。 HPNs将架构重新设计为 3 层原型以进行表示学习。 ERGNN通过存储代表节点来集成记忆重放。 SSM将稀疏化的子图存储在内存库中以保留结构信息。最近为 CGL 开发了两个基准。

C. Graph Condensation 图压缩

数据集压缩生成一个小型合成数据集来替换原始数据集并训练具有相似性能的模型。数据集压缩已应用于计算机视觉。最近，梯度匹配已应用于图压缩，例如 GCond、DosCond和 MCond。DM旨在学习与原始数据集具有相似分布的合成样本，以模仿采样方法。 GCDM使用分布匹配进行图压缩。

最近计算机视觉方面的尝试直接将数据集压缩应用于持续学习，尽管这些方法遵循典型的训练方案，但会陷入不平衡训练。

III. PRELIMINARY

下面，粗体小写字母表示向量，粗体大写字母表示矩阵，普通字母表示标量，脚本化大写字母表示集合。

A. Graph

对于节点分类问题，图表示为 ${\mathbf A,\mathbf X,\mathbf Y}$ ，其中 $\mathbf X \in \mathbb R^{n×d}$ 是 n 个节点的 d 维特征矩阵，邻接矩阵 $\mathbf A \in \mathbb R^{n×n}$ 表示图结构。在本文中，该图是无向且未加权的。 $\mathbf Y \in \mathbb R^{n×1}$ 包括来自类集 C 的节点标签。

B. Graph Neural Networks

图神经网络 (GNN) 是节点分类问题中表示学习的工具。 GNN 中的节点表示是通过聚合来自相邻节点的消息来计算的。 GNN 可以表示为一个函数：

$\mathbf E=\mathrm{GNN}_\theta(\mathbf A,\mathbf X),\quad (1)$

其中 $\theta$ 是模型参数， $\in \mathbb R^{n×d\prime}$ 表示 $d^{'} -$ 维节点嵌入。

C. Graph Condensation 图压缩

图压缩的目的是为大图 $\mathcal G = \{A,X,Y\}$ 合成一个小图 $\mathcal{\tilde G} = \{ \tilde A, \tilde X, \tilde Y\}$ 。使用合成图训练的模型预计具有与原始图相似的性能。这个目标是：

$\min_{\tilde{\mathcal{G}}}\mathcal{L}(\mathcal{G};\tilde{\theta}),\quad\text{s.t. }\tilde{\theta}=\underset{\theta}{\operatorname{arg}\operatorname*{min}}\mathcal{L}(\tilde{\mathcal{G}};\theta),\quad (2)$

其中 $\mathcal L$ 是与任务相关的损失函数，例如交叉熵， $\theta$ 是GNN的参数。

D. Node Classification in CGL CGL中的节点分类

在CGL的节点分类中，需要一个模型来处理 $K$ 个任务 $\{\mathcal{T}_{1},\mathcal{T}_{2},...\mathcal{T}_{K}\}$ 。对于第 $k$ 个任务 $\mathcal{T}_{k}$ ，传入图 $\mathcal G_k$ 到达，模型需要用 $\mathcal G_k$ 更新，同时在所有先前图和传入图上进行测试。遵循[16]、[37]、[44]，设置是传导学习，并且可以很容易地扩展到归纳学习。

CGL问题有两种不同的连续设置，任务增量学习(task-IL)和类增量学习(class-IL)。在task-IL中，模型只需要区分同一任务中的节点。在 IL 类中，模型需要对所有任务中的节点进行分类。Class-IL 更具挑战性，本文重点讨论这一设置，同时也报告了 task-IL 下的整体性能。

E. Imbalanced learning in replay-based CGL methods 基于重放的CGL方法中的不平衡学习

通常，对于基于重放的CGL方法，当将重放的图存储在存储体中时，存在限制每个重放的图的最大节点数量的预算b。在训练阶段，重放的图和传入的图被用来一起训练模型。然而，当传入图的大小明显大于预算时，模型将在传入图上过度扩展。

当前基于重放的CGL方法使用加权损失来解决不平衡问题，其结合了当前任务 $\mathcal{T}_{k}$ 损失 $\mathcal L(\mathcal G_k; \theta_k)$ 和重放图损失 $\mathcal L(\mathcal M_{k−1}; \theta_k)$ 。例如，ER-GNN通过图大小计算权重：

$\ell_{\mathrm{ER-GNN}} =\frac{n_{1:k-1}}{n_{k}+n_{1:k-1}}\mathcal{L}(\mathcal{G}_{k};\theta_{k}) +\frac{n_{k}}{n_{k}+n_{1:k-1}}\mathcal{L}(\mathcal{M}_{k-1};\theta_{k}),\quad(3)$

其中 $n_k$ 和 $n_{1:k−1}$ 分别是输入图 $\mathcal G_k$ 和存储体中的图的节点数。当 $n_{1:k−1} < n_k$ 时， $\mathcal L(\mathcal M_{k−1}; θ_k)$ 被赋予更大的比例因子。学习的重点是记忆库。

SSM(Sparsified subgraph memory for continual graph representation learning)平衡了每个类的大小：

$\ell_{\mathrm{SSM}}=\sum_{c\in\mathcal{C}_{k}}\frac{1}{n_{c}}\mathcal{L}_{c}(\mathcal{G}_{k};\theta_{k})+\sum_{c\in\mathcal{C}_{0:k-1}}\frac{1}{n_{c}}\mathcal{L}_{c}(\mathcal{M}_{k-1};\theta_{k})\quad(4)$

其中 $n_c$ 是属于类别 $c$ 的节点的数量，并且学习将集中于具有较少节点的图。

这两种平衡方法在持续学习过程中都面临着训练问题。在Class-IL设置中，不平衡学习问题主要是由不同类之间的不同样本大小引起的。ER-GNN将限制模型在内存库上学习，一旦整个内存库的大小大大超过传入图的大小。例如，在Arxiv数据集中，当任务对直接缩减训练损失敏感时，SSM会损害当前任务的性能。为了保持SSM的最佳性能，使用等式4只对极不平衡的数据集有效(例如，Reddit和Products)。

IV. METHODOLOGY 方法

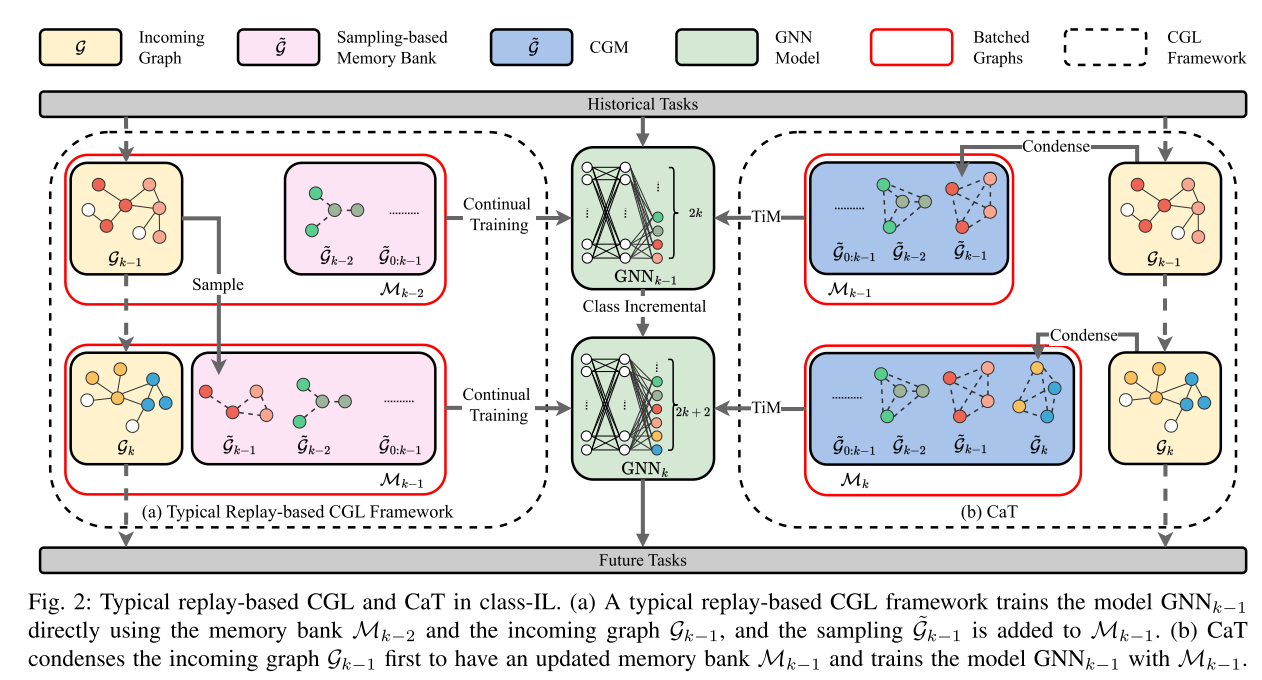
本节描述了拟议的压缩和训练(CaT)框架的详细信息。 CaT 和现有的基于重放的 CGL 方法之间的比较如图 2 所示。现有的基于重放的 CGL方法直接利用传入图来更新和存储存储体中传入图的采样。 CaT 首先压缩传入的图，并使用压缩的图而不是整个传入的图更新模型。

A. Condensed Graph Memory 压缩图形存储器

压缩图存储器(CGM)是一种存储压缩合成图以近似历史数据分布的存储体。在本节中，我们开发具有分布匹配的图压缩，旨在保持合成数据与原始数据相似的数据分布。该方法用作重放图生成方法。

对于任务 $\mathcal T_k$ ，输入图 $\mathcal{G}_{k}=\{\boldsymbol{A}_{k},\boldsymbol{X}_{k},\boldsymbol{Y}_{k}\}$ ，通过图压缩生成压缩图 $\tilde{\mathcal{G}}_{k}=\{\tilde{A}_{k},\tilde{\tilde{X}}_{k},\tilde{Y}_{k}\}$ 。与等式2相比，在分布匹配方案下，这里图压缩的目标函数可以重新表述如下：

$\tilde{\mathcal{G}}_{k}^{*}=\arg\min_{\tilde{\mathcal{G}}_{k}}\mathrm{Dist}(\mathcal{G}_{k},\tilde{\mathcal{G}}_{k}),\quad(5)$

其中 $Dist(\cdot,\cdot)$ 函数计算两个图之间的距离。使用分布匹配，在嵌入空间中测量两个图之间的距离，其中两个图都由相同的图编码器 $GNN_\theta$ 进行编码：

$\begin{aligned}\tilde{\mathcal{G}}_{k}^{*}& ={\operatorname{arg}\operatorname*{min}_{\tilde{\mathcal{G}}_{k}}}(\mathrm{GNN}_{\theta_{k}}(\boldsymbol{A}_{k},\boldsymbol{X}_{k}),\mathrm{GNN}_{\theta_{k}}(\boldsymbol{\tilde{A}}_{k},\boldsymbol{\tilde{X}}_{k}))\quad(6) \\&=\arg\underset{\tilde{\mathcal{G}}_{k}}\min\mathrm{Dist}(\boldsymbol{E}_k,\boldsymbol{\tilde{E}}_k),\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \left(7\right) \end{aligned}$

其中 $\tilde{\mathcal{G}}_k^*=\{\tilde{\boldsymbol{A}}_k^*,\tilde{\boldsymbol{X}}_k^*,\tilde{\boldsymbol{Y}}_k^*\}$ 是最佳重播图，其分布接近输入图的分布。最大平均差异(MMD)用于凭经验计算两个图之间的分布距离。目标是找到MMD的最佳 $\mathcal G_k$ ：

$\ell_{\mathrm{MMD}}=\sum_{c\in\mathcal{C}_{k}}r_{c}\cdot||\mathrm{Mean}(\boldsymbol{E}_{k,c})-\mathrm{Mean}(\boldsymbol{\tilde{E}}_{k,c})||^{2},\quad(8)$

其中 $\mathcal C_k$ 是 $\mathcal G_k$ 中节点类别的集合， $\mathbf E_{c,k}$ 和 $\tilde{\mathbf E}_{c,k}$ 分别是传入图和压缩图的嵌入矩阵，其中所有节点的标签都是 $c_k$ ，并且 $r_{c,k} = \frac{|E_{c,k}|}{|E_{k}|}$ 是 $c_k$ 类的类比。 $|\cdot|$ 是矩阵中的行数。 $Mean(\cdot)$ 是节点嵌入的平均向量。

为了有效地运行压缩过程，这里使用随机 GNN 编码器，而不需要训练 GNN。分布匹配的目标是最小化具有随机参数 $\theta_p$ 的 GNN 给出的不同嵌入空间中的嵌入距离：

$\operatorname*{min}_{\tilde{\mathcal{G}}_{k}}\sum_{\theta_{p}\sim\Theta}\ell_{\mathrm{MMD},\theta_{p}},\quad(9)$

其中 $\Theta$ 表示整个参数空间。CGM的总体流程如算法1所示。

在预算限制为 $b$ 的情况下，压缩图的节点标签 $\tilde{\mathbf Y} \in\mathcal C_b^k$ 被初始化并保持与原始图相同的类比(即对于任何类 $c_k, r_{k,c} \approx \tilde r_{k,c}$ )。使用来自输入图的随机采样来根据分配的标签在开始时初始化压缩节点特征 $\tilde{\mathbf X}_k \in \mathbb R^{b\times d}$ 。初始化也可以作为随机噪声来实现。

B. Train in Memory 记忆训练

在持续学习中，基于重放的普通 CGL 方法面临着不平衡的学习问题。当输入图的大小明显大于重放图的大小时，模型很难平衡历史图和输入图的知识学习。之前的平衡尝试是基于损失缩放。一般形式的等式3和4可以表示为：

$\ell_{\text{replay}}=\alpha\mathcal{L}(\mathcal{G}_k;\theta_k)+\beta\mathcal{L}(\mathcal{M}_{k-1};\theta_k),\quad(10)$

其中，根据不平衡尺度，大部分工作都致力于 $\alpha$ 和 $\beta$ ，这不可避免地损害了性能。

在CaT中，由于CGM能够在不影响性能的情况下压缩图，因此通过使用压缩的输入图而不是整个输入图来解决不平衡问题是合理的。为了将压缩图的这一有益特性融入到平衡训练的持续学习中，当输入图 $\mathcal G_k$ 到达时，首先生成压缩图 $\tilde{\mathcal G}_k$ ，然后用它来更新先前的记忆 $\mathcal M_{k−1}$ ：

$\mathcal{M}_k=\mathcal{M}_{k-1}\cup\tilde{\mathcal{G}}_k.$

CaT 将基于 $\mathcal M_k$ 更新模型，而不是使用 $\mathcal M_{k−1}$ 和 $\mathcal G_k$ 进行训练来处理不平衡问题：

$\begin{aligned} \ell_{\mathrm{CaT}}& =\mathcal{L}(\mathcal{M}_{k};\theta_{k}) \\ &=\mathcal{L}(\tilde{\mathcal{G}}_{k};\theta_{k})+\mathcal{L}(\mathcal{M}_{k-1};\theta_{k}). \end{aligned}\quad\quad (12)$

这个过程被称为内存训练(TiM)，因为该模型仅使用内存库中重放的图进行训练。

综上所述，所提出的CaT框架使用图压缩来生成小而有效的重放图，并应用TiM方案来解决CGL中的不平衡学习问题。 CaT 的总体流程如算法 2 所示。

V. EXPERIMENTS

A. Setup

a) 数据集：继之前的工作之后，实验中使用了四个用于节点分类任务的数据集：CoraFull、Arxiv、Reddit 和 Products。 CoraFull 和 Arxiv 都是引文网络。 Reddit 是一个帖子到帖子图表。产品数据集是共同购买网络。表一显示了这些数据集的统计数据。

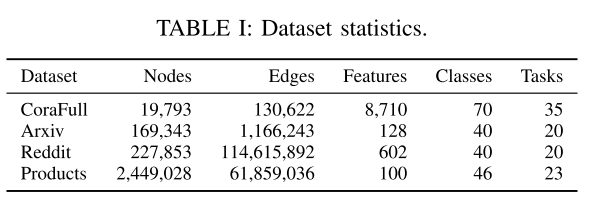
每个数据集被分为一系列专注于节点分类问题的任务。每个任务都包含两个唯一类的节点作为传入图。在每个任务中，选择 60% 的节点作为训练节点，20% 的节点用于验证，20% 的节点用于测试。 Class-IL 是实验的主要焦点，因为它比task-IL 更具挑战性，尽管也会报告task-IL 设置中的整体性能。在持续更新阶段，模型只能访问新传入的图和存储体。在测试阶段，需要使用之前所有任务的测试图来评估模型。任何两个任务之间不存在任务间边缘。在task-IL设置中，模型的输出维度始终设置为2。在class-IL设置中，由于未给出总类数，因此随着新任务的到来，输出维度是增量的。

b) 基线：比较以下基线：

微调(Finetuning)是通过仅使用新传入的图形更新模型来实现下限基线。
联合(Joint)是理想的上限情况，其中存储体包含所有历史传入图表。
EWC 对对先前任务很重要的模型权重应用二次惩罚。
MAS 对对历史任务的模型性能敏感的参数使用正则化项。
GEM 使用存储在内存中的信息数据修改梯度。
TWP 通过正则化项保留先前任务的拓扑信息。
LwF 将旧模型中的知识提炼到新模型中以保留先前的知识。
HPNs 通过维护三级原型重新设计任务IL设置的传统图嵌入生成。尽管 HPN 最近发布，但该基线仅在task-IL 实验中报告。
ER-GNN 将输入图中的信息节点采样到内存库中。
SSM 将稀疏的输入图存储在存储体中以供将来重放。

c) 评估指标：当模型在任务 $\mathcal T_k$ 之后更新时，将评估从 $\mathcal T_1$ 到 $\mathcal T_k$ 的所有先前任务。维护下三角性能矩阵 $\in \mathbb R^{K\times K}$ ，其中 $m_{i,j}$ 表示从任务 $\mathcal T_i (i ≤ j)$ 学习后任务 $\mathcal T_j$ 的分类精度。此外，以下指标用于全面比较不同的方法。

平均性能(Average performance, AP)测量从任务 $\mathcal T_k$ 学习后的平均模型性能：

$\text{AP}_{k}=\frac{1}{k}\sum_{i=1}^{k}m_{k,i}.$

平均性能均值(Mean of average performance, $\overline{AP}$ )表示连续学习过程中模型快照的平均性能：

$\overline{\mathrm{AP}}=\frac{1}{k}\sum_{i=1}^{k}\mathrm{AP}_{i}.$

反向迁移(Backward transfer, BWT)(也称为平均遗忘(AF))表明当前任务的训练过程如何影响先前的任务。较大的数字意味着训练当前任务将对历史任务产生更大的影响。负数或正数分别表示负面或正面影响：

$\text{BWT}_k=\frac{1}{k-1}\sum_{i=1}^{k-1}(m_{k,i}-m_{i,i}).$

d) 执行：预算比率表示整个训练集中内存库与节点总数的比例，每个任务的预算都是均匀分配的。默认情况下，联合基线的预算比率为1，因为它将每个训练数据存储在其内存中。例如，0.01是大多数以下实验中的预算比率，并且存储体的大小变为整个训练数据大小的1%。虽然在更多盗版场景中预算被设置为实数而不是整个训练集的比率，但在实验中使用预算比率是为了保持公平性并比较不同存储体的效率。除非另有说明，对于基于重播的方法，默认预算比率为0.01。

GCN 是默认的骨干模型。对于CGM，使用具有512维隐藏层的 2 层 GCN 对所有四个数据集进行编码，并评估其他图编码器。CoraFull 的压缩特征矩阵的学习率为 0.0001，其他数据集的学习率为 0.01。对于节点分类问题，所有数据集中都使用具有256维隐藏层和类数相关输出层的 2 层 GCN 作为节点分类器。,除非另有说明，所有结果均通过运行 3 次获得，并以平均值和标准误差报告。所有实验均在一台 NVIDIA RTX 2080 Ti GPU上进行。

B. Overall Results

将 CatT 与 class-IL和 task-IL设置中的所有基线进行比较。 AP用于评估任务流结束时所有学习任务的平均模型性能，BWT(也称为平均遗忘(AF))暗示模型在持续学习过程中的遗忘问题。表二显示了class-IL CGL 设置中所有基线和 CatT 的整体性能。与所有其他 CGL 基线相比，CaT 实现了最先进的性能，并且只需维护预算比率仅为 0.01 的合成存储库即可匹配 Arxiv、Reddit 和 Products 中的理想联合性能。此外，结果表明CaT具有较小的BWT，这意味着CaT不仅可以保留模型的历史知识，还可以在训练当前任务的同时减少对先前任务的负面影响，从而缓解灾难性遗忘问题。尽管CaT在CoraFull中的性能优于其他基线，但CaT没有达到联合性能有两个潜在原因：(1) CoraFull的0.01预算比率将重播图限制为四个节点，该节点非常小，无法包含足够的信息；(2) CoraFull有35个任务，比其他数据集多，并且难以保留历史知识。

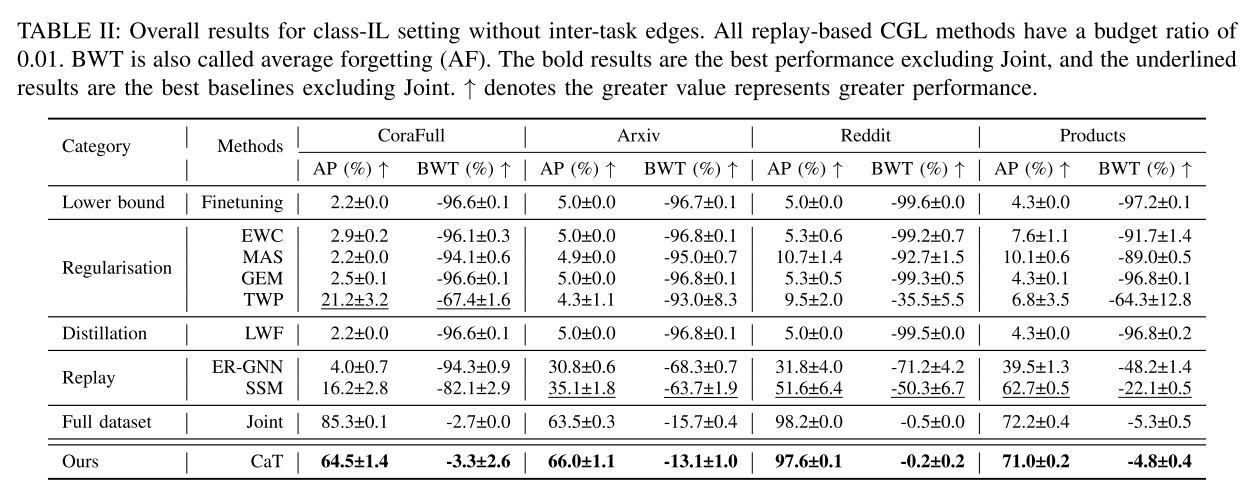
其他基线很难与CaT的性能相匹配。Finetuning很容易忘记以前的知识，因为它只使用新传入的图来更新模型。基于监管的方法(例如，EWC、MAS、GEM、TWP)也具有不令人满意的性能，因为向模型添加开销限制将导致在长流任务期间的模型可塑性差。作为一种蒸馏方法，LwF几乎不能处理CGL中的class-IL设置。由于存在严重的不平衡训练问题，ERGNN在基于采样的重放方法的所有基准测试中都没有合理的结果。SSM将稀疏化的子图存储在内存库中，可以保存历史图数据的拓扑信息。虽然SSM具有良好的性能，但与Joint或CaT相比仍有差距。

值得注意的是，尽管所有历史数据都可以用于训练，但Joint也有负BWT。原因是class-IL设置要求模型在新类出现时增加输出层维度，其中模型不能完全记住所有先前的知识。未提供class-IL的 HPN 结果，因为它不是为class-IL设置而设计的。

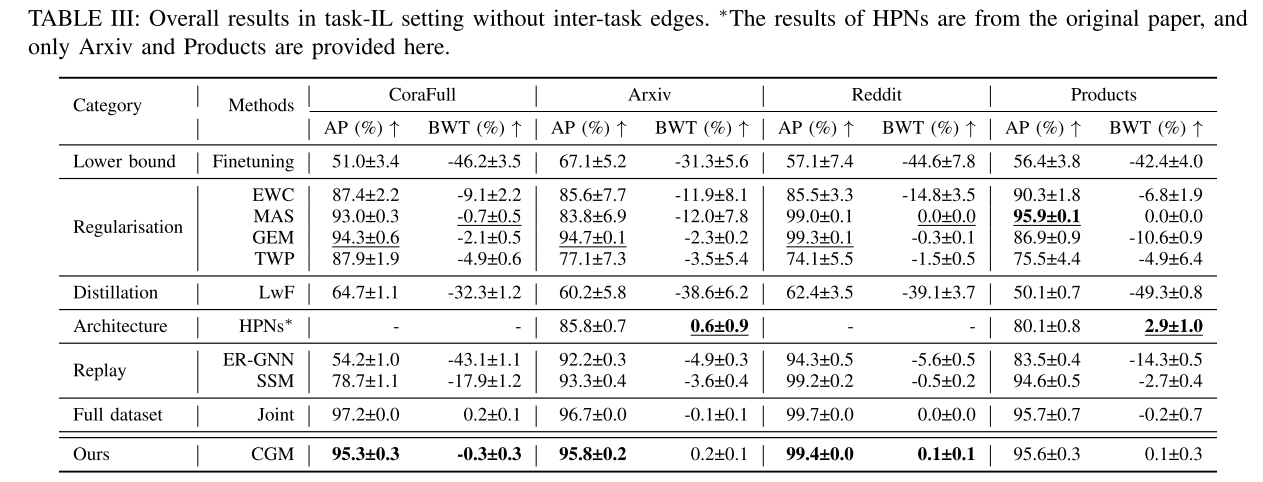
表三显示了task-IL设置下的整体性能。与class-IL设置相比，task-IL要容易得多，并且所有基线方法都得到合理的结果。Cat 实现了最先进的性能，并且只需 0.01 的预算比即可与联合方法相媲美。

C. Ablation Study 消融研究

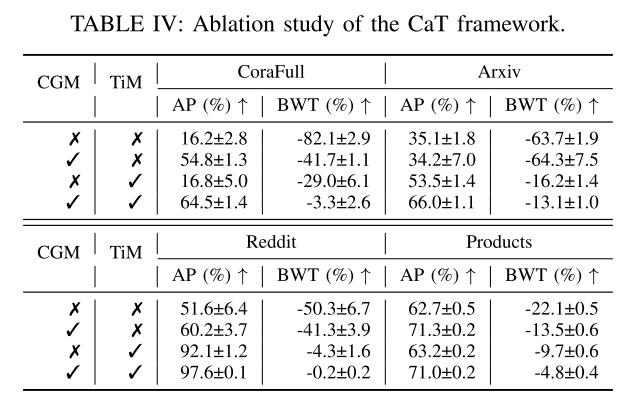
CaT框架有两个关键组件：CGM 和 TiM。为了研究它们的有效性，评估了不同的 CaT 变体，这些变体的 AP 和 BWT 报告在表 IV 中。不带 CGM 的变体表示对存储体使用随机选择，不带TiM 的变体表示使用整个传入图进行训练的典型的基于重放的方案。根据表 IV，与没有这两种组件的变体相比，使用 CGM 的变体在 CoraFull 和 Arxiv 数据集中提高了 AP 和 BWT，但在 Reddit 和 Products 数据集中有所下降。主要原因是 CoraFull 和 Arxiv 都是小型数据集，CGM 可以轻松捕获数据分布。CGM 对大型数据集的模型几乎没有好处，尤其是在规模不平衡问题占主导地位的产品数据集中。与不带 TiM 的变体相比，带 TiM 的变体显着提高了整体性能，尤其是在大型数据集(例如 Reddit 和 Products)上。这也体现了TiM对于不平衡图的有效性。

D. Effectiveness and Efficiency of CGM CGM 的有效性和效率

为了分析 CGM 的有效性和效率，使用四个预算比率(即 0.005、0.01、0.05 和 0.1)评估不同的存储体。具体来说，0.005 是一个极其有限的预算比率，在该比率下，CGM 仅包含 CoraFull 数据集上的 2 节点重播图。而0.1是一个大的预算比率，它代表存储体的大小等于整个训练集大小的10%。为了与 CatT 进行公平比较，TiM 方案应用于 ER-GNN 和 SSM。EatT和SaT用来表示带有TiM的ER-GNN，简称带有TiM的SSM。这里使用的是AP。

a) 不同的存储体：图 3 表明 CGM 比现有的基于采样的存储体更有效。CGM 更快地收敛到最佳性能。CGM 在所有评估案例中几乎获得了最佳性能。当预算比率相对较小(例如 0.005、0.01)时，CGM 显着优于其他基于采样的存储体。尽管在Arxiv数据集中，当预算比率大到0.1时，SSM可以优于CGM，这对于记忆体来说是不切实际的。此外，CGM 的标准误差很小，这表明 CGM 对于持续训练来说更加稳健。在 CoraFull 数据集中，0.01 预算的 AP 略低于 0.005。预算为 0.01(4 节点重放图)和预算为 0.005(2 节点重放图)的重放图大小相似。唯一的区别是 2 节点重放图具有统一的类分布，但 4 节点重放图保持与原始图相同的类分布。潜在的原因是小回放图中提出的类别不平衡问题。我们将类之间的平衡作为未来的研究问题。

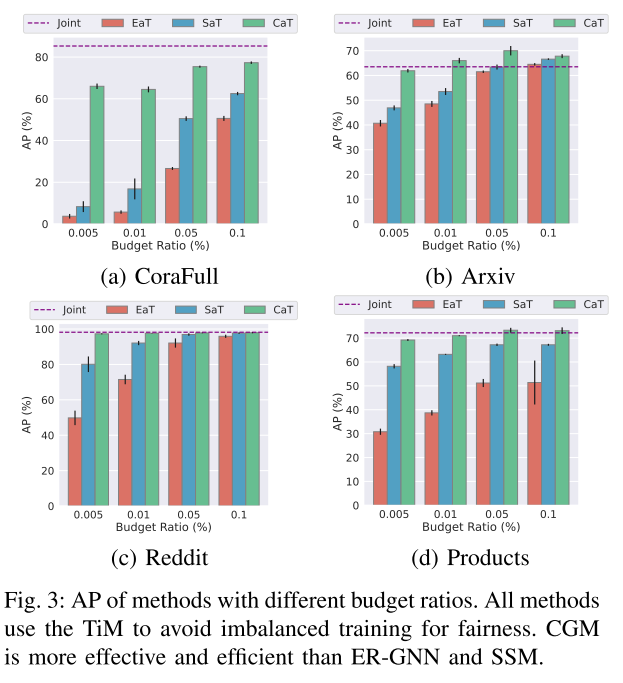
b) 预算效率：压缩图的优点是保留原始图的信息，同时显着减小图的大小。图 3 显示，CGM 方法在更有限的预算内实现更高的性能方面优于基于采样的方法。在所有数据集中，基于采样的方法与 CGM 都有巨大的性能差距。0.005 预算比率 CGM 可以优于或匹配基于 0.1 预算比率抽样的方法。

一方面，CGM 使用较少的内存空间来准确地近似历史数据分布。另一方面，在训练阶段，模型需要在记忆库中传播消息。因此，小的存储体可以提高存储和计算效率。

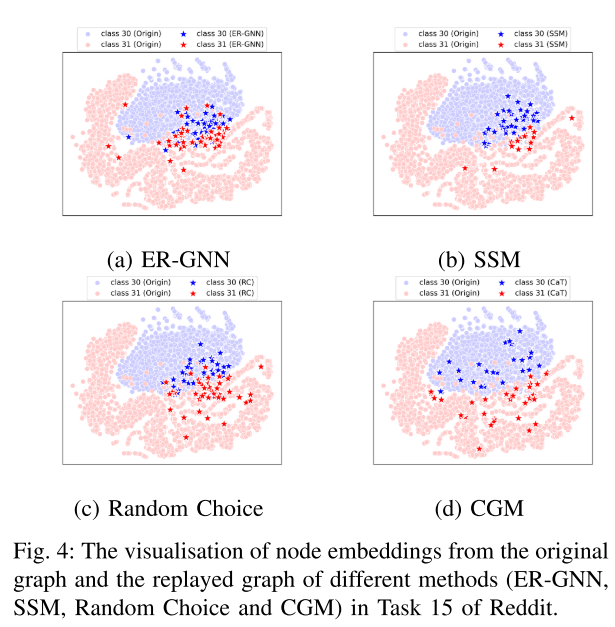
c) 可视化：进一步探讨 CGM 的有效性。 t-SNE 在图 4 中可视化了不同存储体的节点嵌入，其中显示了 ER-GNN、SSM、CGM 初始化(随机选择)和 CGM 的嵌入分布。为了保持相同的嵌入空间以进行合理的比较，所有节点嵌入都是使用相同的图编码器生成的。基于采样的存储体中的节点嵌入彼此接近，无法有效地近似完整的图分布。相反，CGM的嵌入更加多样化，可以覆盖整个分布，使得分类模型能够学习到更准确的决策边界。

E. Balanced Learning with TiM 使用 TiM 平衡学习

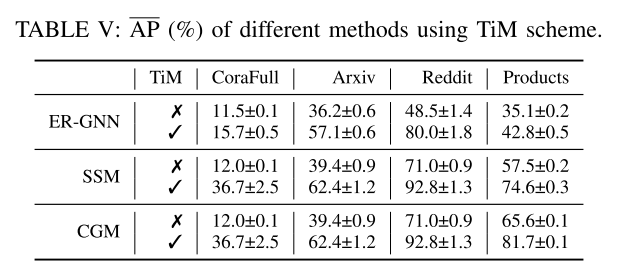
a) TiM 的不同方法：TiM 是一种即插即用的训练方案，适用于所有现有的基于重放的 CGL 方法。表 V 显示了使用和不使用 TiM 的不同基于重放的 CGL 方法的 AP 平均值。它清楚地表明 TiM 方案可以提高所有存储体生成方法的整体平均性能。原因是TiM可以确保CGL模型的训练图具有相似的大小来处理不平衡问题，从而可以解决灾难性遗忘问题。

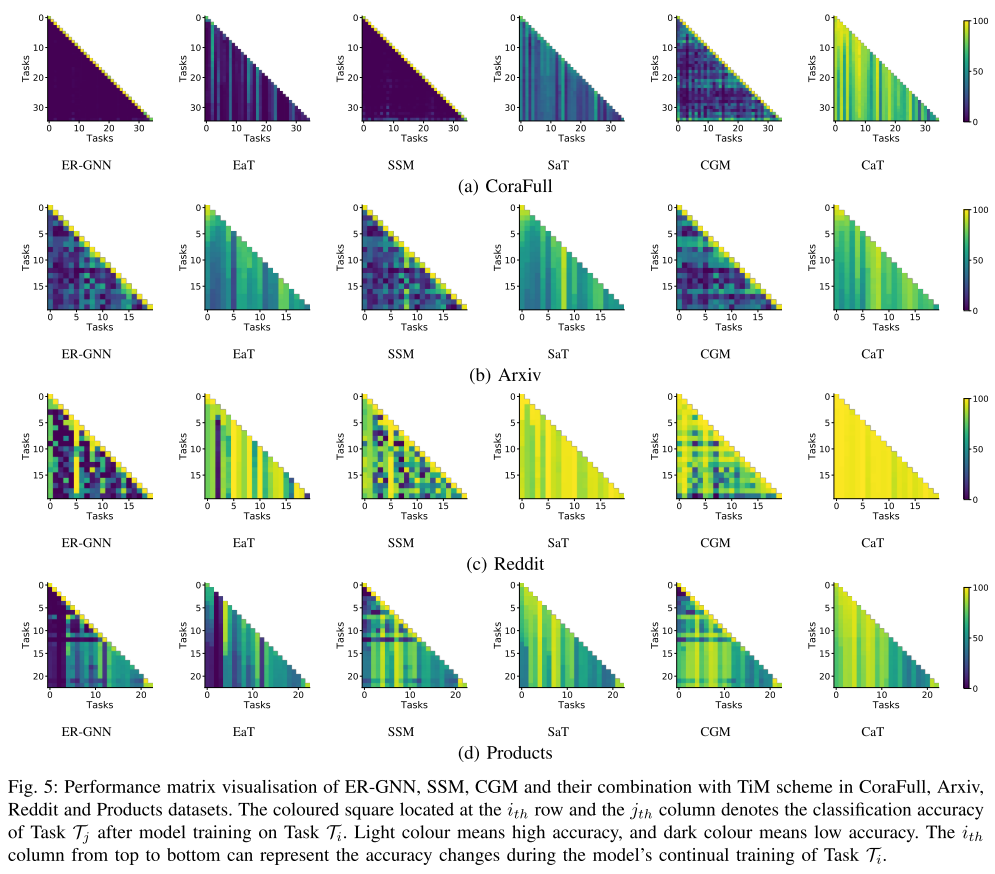
b) 可视化：预算比率为 0.01 的情况下，ER-GNN、SSM、CGM 以及在 CoraFull、Arxiv、Reddit 和 Products 数据集上使用 TiM(即 EaT、SaT can CaT)训练的记忆库的性能矩阵如图5所示。所有没有 TiM 的记忆体都很难记住以前的知识，因为记忆体中新传入的图和重放的图之间存在规模差距。使用TiM方案后，性能矩阵显示遗忘过程减慢(即每列的颜色没有太大变化)，这表明随着不平衡训练问题的解决，灾难性遗忘问题得到缓解。

F. Parameter Sensitivity 参数灵敏度

CGM 中有几个超参数，包括重放图的预算，该预算已在图 3 中进行了评估。本节将讨论图编码器的选择。

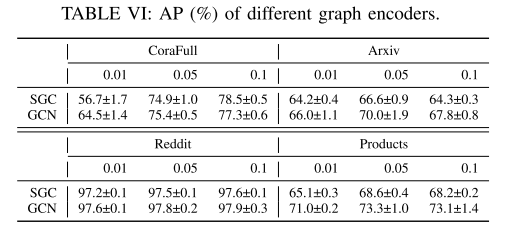
a) 不同的图编码器：本实验将比较 GCN 和 SGC 作为 CGM 的编码器，而 GCN 仍将应用于 CGL 的节点分类。AP用于衡量有效性。所有 CGM 编码器都有一个 256 维隐藏层和一个 128 维输出层。表六显示，对于不同的预算比率，SGC 和 GCN 可以作为 CGM 的竞争编码器。一个例外是，在预算比率为0.01的CoraFull中，使用SGC的CGM的性能远低于使用GCN的CGM。这是可能的，因为 0.01 对于 CoraFull 数据集来说是一个非常严格的预算比率，SGC 在如此少的数据下不具备足够的表示能力。类似的情况也发生在 Products 数据集中，这对于 GNN 来说是一个巨大且具有挑战性的数据集。

VI. CONCLUSION

本文指出了基于重放的 CGL 方法中基于采样的内存库效率低下和持续学习不平衡的问题。为了解决这些问题，提出了一种新颖的CaT框架，其中包括两个关键组件：CGM和TiM。CGM 是一个基于图压缩的小而有效的存储库。TiM 方案用新传入的图更新存储体，并用该存储体不断训练模型以平衡更新。大量实验表明该框架在class-IL 和task-IL设置中实现了最先进的性能。