由于最近在整理单目测距的内容，顺手也总结下鱼眼相机的测距流程和误差分析，如果有错误，还请不吝赐教。

参考链接:
鱼眼镜头的成像原理到畸变矫正（完整版）
相机模型总结（针孔、鱼眼、全景）
三维空间中判断射线与平面是否相交
相机外参标定误差对目标测距的影响分析（待整理）
像素坐标转到世界坐标时相机坐标系中的Zc值求解
一文简要介绍鱼眼镜头/相机投影成像过程
一文详解分析鱼眼相机投影成像模型和畸变模型
相机模型-鱼眼模型（fisheye camera model）
SLAM 中常用的相机模型&畸变模型总结

最后两位大哥写的特别好,原理部分写的很详细也很全，我就不打算复制粘贴了，我从归一化坐标开始写，感谢大佬们的无私奉献！！

1 投影过程

2 反投影过程

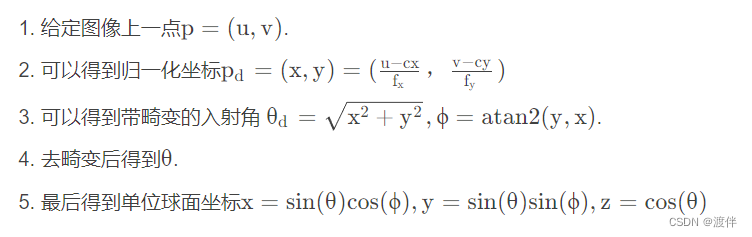
我这里是像素坐标系转世界坐标系，对应着反投影过程，到第五步已经得到单位球面坐标系里的位置。

这里分两种方法:

1. 根据 像素坐标转到世界坐标时相机坐标系中的Zc值求解 这位作者写的，先计算出Zc的值，再根据像素坐标算出世界坐标系的位置，作者也给出了python的代码，目前我觉得思路没啥问题。
2. 推导从相机光心出发，通过像素点(u, v)的射线与地面的交点，解出交点，这个交点就是像素坐标系转到世界坐标系的位置。

很重要的几个知识点:

1. 鱼眼相机成像模型近似为单位球面投影模型。根据投影函数的不同将鱼眼相机的设计模型大致分为等距投影模型、等立体角投影模型、正交投影模型和体视投影模型四种。相机的成像模型实际上表征的是成像的像高与入射角之间的映射关系。
2. 不管是针孔相机模型，还是鱼眼相机模型，其成像过程都涉及到四个坐标系：世界坐标系、相机坐标系、图像物理坐标系、图像像素坐标系以及这四个坐标系间的转换。具体的成像原理请看参考文献，大佬们写的非常好。
3. 鱼眼相机和针孔相机成像的不同之处: 在鱼眼模型中会将相机下的空间点, 先转换为归一化相机球面上，再从球面投影到平面上。针孔相机将空间点直接投影到平面上。
4. 不管是鱼眼相机模型还是针孔相机模型(我目前接触过的两种相机，其他相机没仔细研究过), 假设在图像平面中有一个接地点的像素坐标P=(u, v), 将该点转换为归一化相机坐标系下的点Pc，由于Pc是归一化坐标，它实际上代表了从相机光心出发，通过像素点P=(u, v)的射线方向。这条射线与地平面 (Z=0) 的交点就是接地点的3D位置。[写到这里是不是很清楚了，看到了啥，射线方程啊，兄弟们！！所以要做的事情就是推导出这个交点，求解出交点，有了这个交点要测距的话就算出距离]

3 推导射线与地面交点

3.1 归一化相机坐标系下的射线：

设归一化坐标系下的射线方向向量为d,t 表示射线上的一点距离相机光心的标量，表示沿射线的距离，那么在归一化相机坐标系下，相机作为原点，所以射线的方程可以表示为：
Pc(t) = t * d

3.2 射线在世界坐标系下的表示：

将射线从相机坐标系转换到世界坐标系，R是相机旋转矩阵, T 是相机的平移向量：
Pw(t) = R * Pc(t) + T

4 求解射线与地面交点

射线与地面的交点在世界坐标系下的 Z 值为 0，因此：
Pw(t)(z) = 0 就是z为0
( R * Pc(t) + T)(z) = 0 就是把上面那个公式带了进来
( R * t * d + T)(z) = 0 那个Pc(t) 带了进来
t * (R * d)z + Tz = 0 这些都是可以立即推的

即射线方向向量在世界坐标系下的表示：dw = R * d
解出t：

$t=-\frac{T_z}{(d_w{)}_z}$$=-\frac{z_c}{d_{w,z}}$

现在有了射线方向dw和沿着射线的距离t，可以找到交点Pw:
$P_w=R\cdot (-\frac{T_z}{(d_w{)}_z}\cdot d)+T$
$P_w=R\cdot (-\frac{z_c}{d_{w,z}}\cdot d)+T$

4.1 计算距离:

最后，计算交点Pw与相机在 XY 平面上的投影距离。相机的位置是(xc, yc, zc),
$dist=\sqrt{(P_{w,x}-T_x{)}^2+(P_{w,y}-T_y{)}^2}$

1. 这个计算假设地面是平坦的，并且与 XY 平面对齐。在实际情况中，地面可能不完全平坦，或者与 XY 平面不是完全对齐的，需要额外的校正。
2. 以上便是基于针孔相机模型的测距推导完整过程，基于这个过程可以用来研究相机外参参数对测距结果的具体影响。
   

总结：

1. 别人也做了实验验证误差部分，我没做实验我也不贴别人的结论了。
2. 很长时间内，我都不明白为啥我算出来的3D位置总是有问题，我拿到的3D位置跟激光雷达给出来的误差那么多，我一直觉得我的射线方程部分没写错，就今天我才知道我错哪里了。Pw的方程那边一定要写对，我就是解 t 的时候代码里少了负号，死活找不到原因，死活觉得我的理论没问题啊。真的是哪哪都对，就是结果不对。非常确定自己的理论没问题就去看看自己写的代码，一行一行看，没准有惊喜。