一、简介

树状数组用于两种操作：

1. 快速求前缀和$O(logn)$
2. 修改某一个数$O(logn)$

这两个操作也可以用其他方法结构完成：
用一个数组存每个数：操作1.$O(n)$，遍历前n个数求和；操作2. $O(1)$，直接修改即可
维护前缀和一个数组：操作1.$O(1)$；操作2. $O(n)$

可见其他结构最坏情况都是$O(n)$

二、算法

已知一个数可以拆成若干个2的幂次之和
$x=2^{i_1}+2^{i_2}+2^{i_3}+...+2^{i_k}$
其中$i_1\le i_2\le ...\le i_k$
所以区间$(0,x]$可以拆成

$(x-2^{i_1},x]$
$(x-2^{i_1}-2^{i_2},x-2^{i_1}]$
.
.
.
$(x-2^{i_1}-2^{i_2}-...-2^{i_k},x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}]$
也就是
$(0,x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}]$

再来看这些区间包含多少个数
$(x-2^{i_1},x]$包含$2^{i_1}$个数，其中$i_1$是$x$二进制表示的最后一位1的位置
$(x-2^{i_1}-2^{i_2},x-2^{i_1}]$包含$2^{i_2}$个数，其中$i_2$是$x-2^{i_1}$二进制表示的最后一位1的位置
$(0,x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}]$包含$2^{i_k}$个数，其中$i_k$是$x-2^{i_1}-2^{i_2}-...-2^{i_{k-1}}$二进制表示的最后一位1的位置。

性质1：对于区间$(L,R]$，区间包含的数的个数是R的二进制表示的最后一位1的位置对应次幂。

这个最后一位1的位置对应次幂可以用lowbit(x) = x & (-x)计算求得，因为计算机里的负数就是对原数的二进制取反+1

例如：$6=110_2$，$-6=010_2$，lowbit(6) = 110 & 010 = 10，即6最后一位1对应次幂是$10_2=2^1$

再来看如何拆分区间：$x=6=2^2+2^1$，二进制是$110_2$，因此$i_1=1$，$i_2=2$
所以区间$(0,6]$可以拆成：
$(6-2^1,6]=(4,6]$，其中$i_1=1$是$6$二进制表示$110$最后一位1的位置
$(6-2^1-2^2,x-2^2]=(0,4]$，其中$i_2=2$是$4$二进制表示$100$最后一位1的位置

有了性质1，可以得到$L=R-lobit(R)$，故区间为$(R-lobit(R),R]$

---

用数组$t[x]$表示区间$[x-lobit(x)+1,x]$的和，则$t[0]$~$t[8]$如下所示
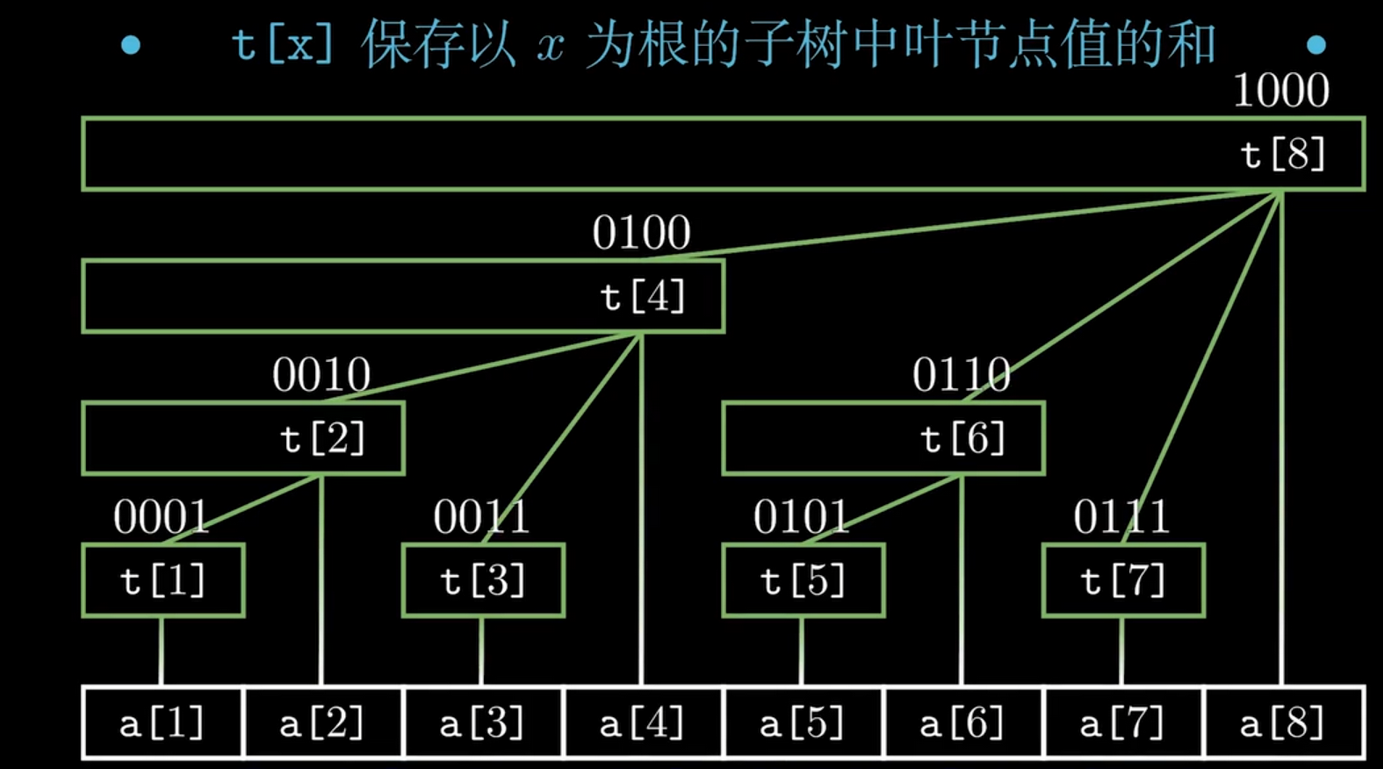可以看到形成一个类似树的结构，例如t[8]的孩子就有$t[4],t[6],t[7]$。

---

这个树有如下性质：

性质2：
通过父节点$t[x]$找子节点：令$x^{\prime }=x-1$，之后不断去掉$x^{\prime }$的最后一位1即可。
即对于$x=...10...000_2$，得到$x^{\prime }=x-1=...01...111_2$，所以有孩子$...01...111_2$、$...01...110_2$、$...01...100_2$、$...01...000_2$、…、$...00...000_2$

例如$t[8]$，得到$x^{\prime }=1000_2-1_2=111_2$，则孩子有$t[111_2],t[110_2],t[100_2]$也就是$t[7],t[6],t[4]$
通过性质2，可以由孩子求出父亲，例如$t[8]=a[8]+t[4]+t[6]+t[7]$
查询a[1] + ... + a[x] -> for(int i = x; i > 0; i -= lobit(i)) sum += t[i]

性质3：
通过子节点找父节点：将父节点找子节点过程逆过来即可
对于孩子$x=...01...100_2$，父亲一定是$...10...000_2$，可以看到孩子只有唯一一个父亲
所以只需$...01...100_2+...00...100_2$即可得到父亲$...10...000$
也就是x + lobit(x)
通过性质3，可以找到更新原数组时所需要更新的对应的树状数组
原数组修改a[x] += c -> 树状数组修改for(int i = x; i <= n; i += lobit(i)) t[i] += c

注意：树状数组维护的位置下表只可以从1开始，如果为0则的lowbit也是0，会死循

---

三、例题

树状数组模板

注意

#include <iostream>
using namespace std;const int N = 500005;
int n, m;
int t[N], a[N];int lowbit(int x) {return x & (-x);
}int sum(int x) {int s = 0;for (int i = x; i > 0; i -= lowbit(i))   s += t[i];return s;
}void add(int x, int c) {for (int i = x; i <= n; i += lowbit(i)) {t[i] += c;}
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) {scanf("%d", &a[i]);add(i, a[i]);}int op, x, y;for (int i = 1; i <= m; i ++ ) {scanf("%d%d%d", &op, &x, &y);if (op == 1) {add(x, y);}else {printf("%d\n", sum(y) - sum(x - 1));}}return 0;
}