💕"对相爱的人来说,对方的心意,才是最好的房子。"💕
作者:Lvzi
文章主要内容:算法系列–递归,回溯,剪枝的综合应用(2)
大家好,今天为大家带来的是
算法系列--递归,回溯,剪枝的综合应用(2)
一.括号⽣成
题目链接
括号生成
题目描述
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例:
-
输入:n = 3
输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] -
输入:n = 1
输出:[“()”]
提示:
- 1 <= n <= 8
分析:

代码:
class Solution {List<String> ret;// 返回值StringBuffer path;// 记录搜索路径int maxLevel, lcnt, rcnt;// max表示最大层数 lcnt表示左括号的数量 rcnt表示右括号的数量public List<String> generateParenthesis(int n) {ret = new ArrayList<>();path = new StringBuffer();if (n == 0) return ret;maxLevel = 2 * n;dfs(1, lcnt, rcnt,n);return ret;}private void dfs(int level, int lcnt, int rcnt,int n) {// 递归出口if(level > maxLevel) {ret.add(path.toString());return;}if(lcnt < n) {path.append("(");dfs(level + 1,lcnt+1, rcnt,n);path.deleteCharAt(path.length() - 1);// 回溯}if(rcnt < n && lcnt > rcnt) {path.append(")");dfs(level + 1, lcnt, rcnt+1,n);path.deleteCharAt(path.length() - 1);// 回溯}}
}
二.目标和
题目链接
目标和
题目描述
给你一个非负整数数组 nums 和一个整数 target。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个表达式:
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。
示例:
-
输入:
nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有5种方法让最终目标和为3。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3 -
输入:
nums = [1], target = 1
输出:1
提示:
- 1 <= nums.length <= 20
- 0 <= nums[i] <= 1000
- 0 <= sum(nums[i]) <= 1000
- -1000 <= target <= 1000
分析:
思路同子集相同,子集中我们的决策策略是选不选当前的数,本题采用+当前数/-当前数

代码:
class Solution {int path, ret, target;public int findTargetSumWays(int[] nums, int _target) {target = _target;dfs(nums,0);return ret;}private void dfs(int[] nums, int pos) {if(pos == nums.length) {if(path == target) ret += 1;return;}// +path += nums[pos];dfs(nums,pos + 1);path -= nums[pos];//回溯// -path -= nums[pos];dfs(nums,pos + 1);path += nums[pos];// 回溯}
}
本题的最优解法其实是动态规划,具体可见我的这篇文章
算法系列–动态规划–背包问题(2)–01背包拓展题目
(有限制条件下的组合问题,且一个数只能选择一次–01背包问题)
3.组合总和
题目链接
组合总和
题目描述
给你一个无重复元素的整数数组 candidates 和一个目标整数 target,找出 candidates 中可以使数字和为目标数 target 的所有不同组合,并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例:
-
输入:
candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。 -
输入:
candidates = [2,3,5], target = 8
输出:[[2,2,2,2],[2,3,3],[3,5]] -
输入:
candidates = [2], target = 1
输出:[]
提示:
- 1 <= candidates.length <= 30
- 2 <= candidates[i] <= 40
- candidates 的所有元素互不相同
- 1 <= target <= 40
分析:
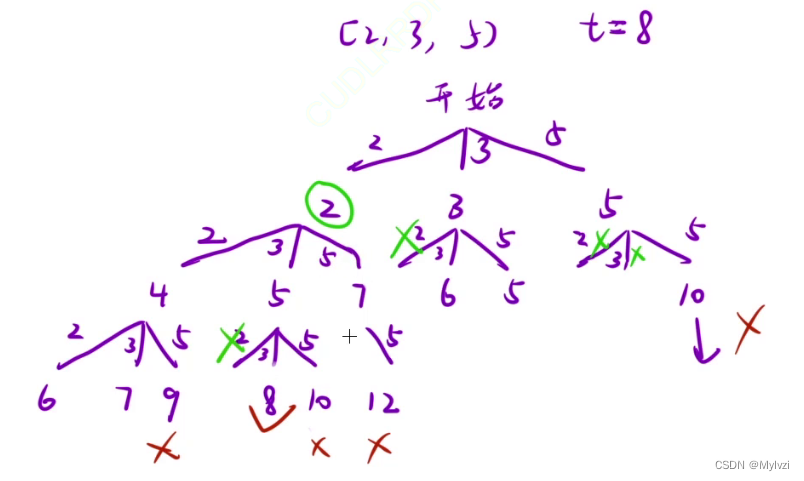
(如果本题是要求组合总和的最多组合数就是一个完全背包问题)
代码:
class Solution {List<List<Integer>> ret;List<Integer> path;// 保存搜索路径int sum, target;// sum记录搜索路径上的和public List<List<Integer>> combinationSum(int[] nums, int _target) {ret = new ArrayList<>();path = new ArrayList<>();target = _target;dfs(nums,0);return ret;}private void dfs(int[] nums, int pos) {if(sum >= target) {// 递归出口if(sum == target) {ret.add(new ArrayList<>(path));}return;}for(int i = pos; i < nums.length; i++) {path.add(nums[i]); sum += nums[i];dfs(nums,i);// 递归path.remove(path.size() - 1); sum -= nums[i];// 回溯}}
}
4.字⺟⼤⼩写全排列
题目链接
字⺟⼤⼩写全排列
题目描述
784. 字母大小写全排列
给定一个字符串 s,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回所有可能得到的字符串集合。以任意顺序返回输出。
示例:
-
输入:s = “a1b2”
输出:[“a1b2”, “a1B2”, “A1b2”, “A1B2”] -
输入: s = “3z4”
输出: [“3z4”,“3Z4”]
提示:
- 1 <= s.length <= 12
s由小写英文字母、大写英文字母和数字组成
解题思路
这道题可以使用回溯算法来解决。我们可以逐个遍历字符串中的每个字符,然后对于每个字符有两种选择:保持原大小写或者转换大小写。通过递归实现所有可能的组合。
代码实现(Java)
class Solution {List<String> ret;StringBuffer path;public List<String> letterCasePermutation(String s) {ret = new ArrayList<>();path = new StringBuffer();dfs(s,0);return ret;}private void dfs(String s, int pos) {if(pos == s.length()) {ret.add(path.toString());return;}// 不改变char ch = s.charAt(pos);path.append(ch);dfs(s, pos + 1);path.deleteCharAt(path.length() - 1);// 改变(非数字字符)if(ch < '0' || ch > '9') {char tmp = change(ch);path.append(tmp);dfs(s, pos + 1);path.deleteCharAt(path.length() - 1);}}private char change(char ch) {if(ch >= 'a' && ch <= 'z') return ch -= 32;else return ch += 32;}
}
5.优美的排列
题目链接
优美的排列
题目描述
526. 优美的排列
假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm(下标从 1 开始),只要满足下述条件之一,该数组就是一个优美的排列:
- perm[i] 能够被 i 整除
- i 能够被 perm[i] 整除
给你一个整数 n ,返回可以构造的优美排列的数量。
示例:
输入:n = 2
输出:2
解释:
- 第 1 个优美的排列是 [1,2]:
- perm[1] = 1 能被 i = 1 整除
- perm[2] = 2 能被 i = 2 整除
- 第 2 个优美的排列是 [2,1]:
- perm[1] = 2 能被 i = 1 整除
- i = 2 能被 perm[2] = 1 整除
解题思路
这道题可以使用回溯算法来解决。我们可以尝试将数字填充到数组的每个位置上,同时检查当前位置是否满足条件。如果满足条件,继续递归处理下一个位置;否则,回溯到上一个位置重新尝试其他数字。
check[i]:用于标记数字是否被使用过ret:返回值
代码实现(Java)
class Solution {int ret;// 返回值boolean[] check;// 用于标记已经使用过的数字public int countArrangement(int n) {check = new boolean[n + 1];dfs(1,n);return ret;}private void dfs(int pos, int n) {// pos是下标if(pos == n + 1) {// 递归出口ret += 1;return;}for(int i = 1; i <= n; i++) {if(check[i] == false && (pos % i == 0 || i % pos == 0)) {check[i] = true;// 将使用过的数字标记dfs(pos + 1, n);// 递归下一个位置check[i] = false;// 回溯}}}
}
在这段代码中:
pos表示当前递归到的位置,也就是在填充数组时当前正在考虑的位置。i则表示尝试填充到当前位置pos上的数字。
具体来说:
pos从1开始,代表数组中的位置,递归函数会尝试将数字填充到这些位置上。i从1到n,代表可以填充到当前位置的数字,即数组中的元素。
6. 组合
题目链接
组合
题目描述
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按任何顺序返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
- 1 <= n <= 20
- 1 <= k <= n
分析:
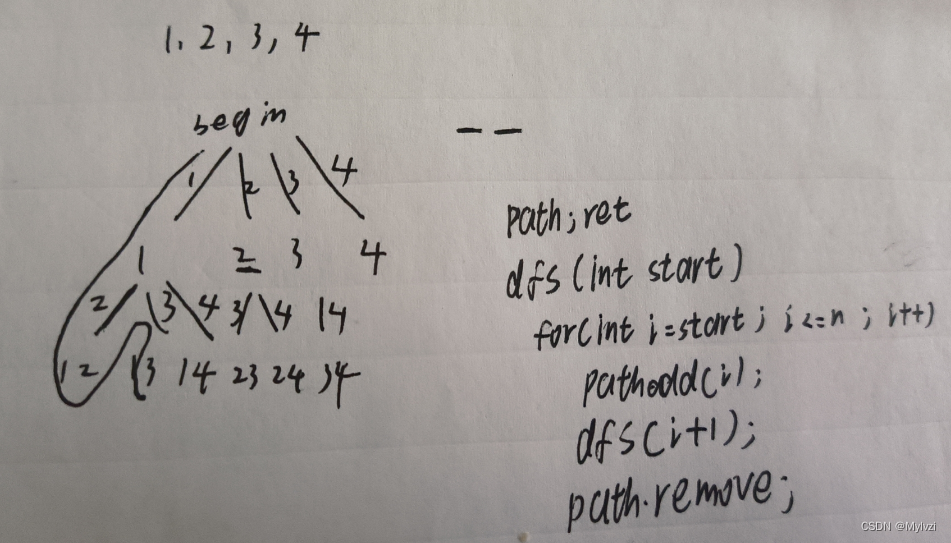
代码:
class Solution {List<List<Integer>> ret;List<Integer> path;int k, n;public List<List<Integer>> combine(int nn, int kk) {n = nn; k = kk;ret = new ArrayList<>();path = new ArrayList<>();dfs(1);return ret;}private void dfs(int start) {if(path.size() == k) {ret.add(new ArrayList<>(path));return;}for(int i = start; i <= n; i++) {path.add(i);// 添加当前数字dfs(i + 1);// 递归下一个数字path.remove(path.size() - 1);// 回溯}}
}
总结:
- 对于递归回溯这样的问题,一定要把决策树画的详细,要明确每一步的目的是什么,是根据什么进行递归的