代码随想录训练营day27

第七章回溯算法part03

1.LeetCode.

1.1题目链接：39. 组合总和

文章讲解：代码随想录
视频讲解：B站卡哥视频

1.2思路：题目中的无限制重复被选取，吓得我赶紧想想出现0 可咋办，然后看到下面提示：1 <= candidates[i] <= 200，我就放心了。本题和77.组合 (opens new window)，216.组合总和III (opens new window)的区别是：本题没有数量要求，可以无限重复，但是有总和的限制，所以间接的也是有个数的限制。

本题搜索的过程抽象成树形结构如下：
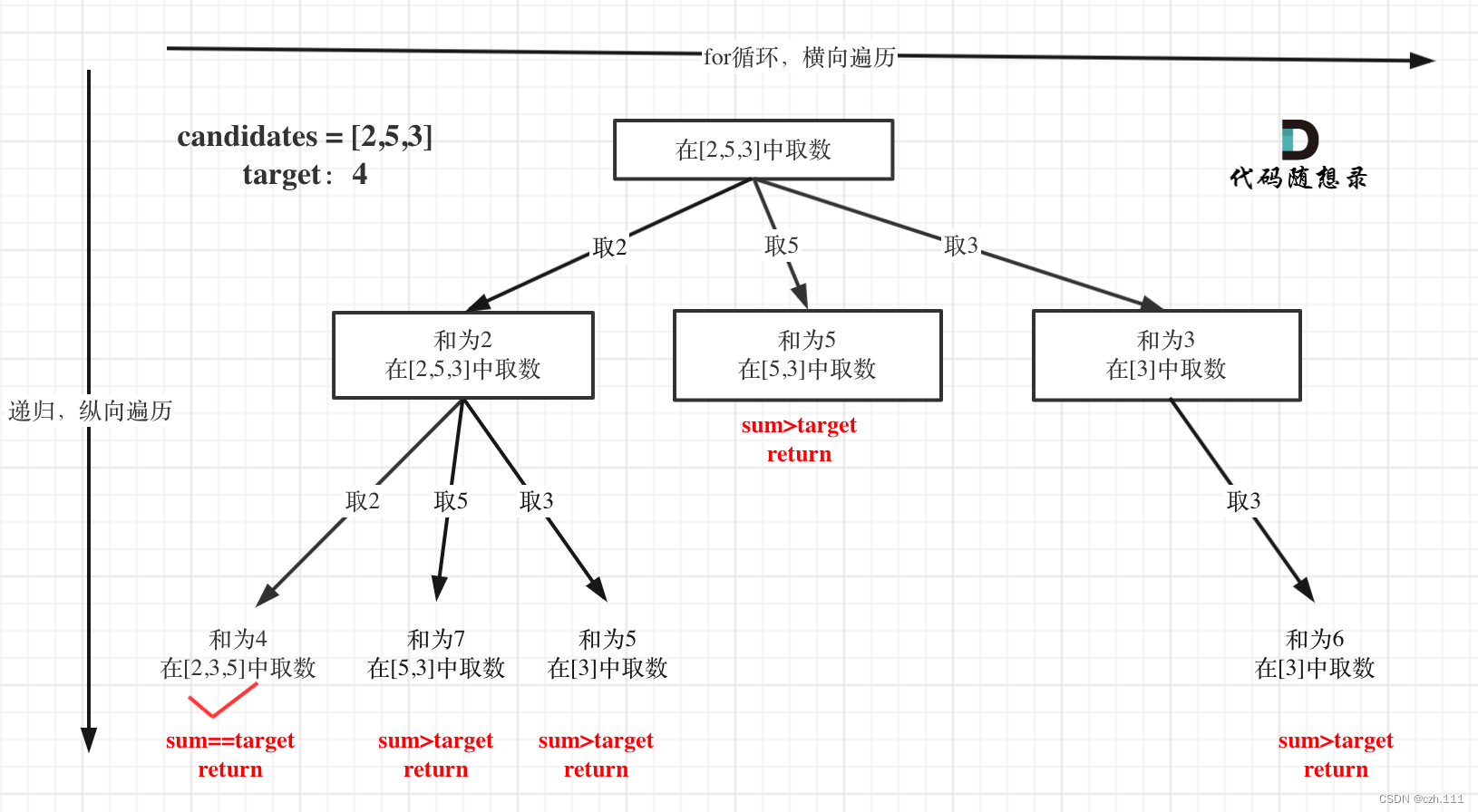
在这里插入图片描述
注意图中叶子节点的返回条件，因为本题没有组合数量要求，仅仅是总和的限制，所以递归没有层数的限制，只要选取的元素总和超过target，就返回！

1.3附加代码如下所示：

//递归法
class Solution {
public:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>&candidates,int target,int sum,int startindex){if(sum>target)return;if(sum==target){result.push_back(path);return;}for(int i=startindex;i<candidates.size();i++){path.push_back(candidates[i]);sum+=candidates[i];backtracking(candidates,target,sum,i);//由于元素可重复 所以startindex要从i开始path.pop_back();//回溯sum-=candidates[i];//回溯}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {result.clear();path.clear();backtracking(candidates,target,0,0);return result;}
};

2.LeetCode. 有效的字母异位词

2.1题目链接：40.组合总和II

文章讲解：代码随想录
视频讲解：B站卡哥视频

2.2思路：本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。一些同学可能想了：我把所有组合求出来，再用set或者map去重，这么做很容易超时！所谓去重，其实就是使用过的元素不能重复选取。这么一说好像很简单！都知道组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。没有理解这两个层面上的“使用过” 是造成大家没有彻底理解去重的根本原因。那么问题来了，我们是要同一树层上使用过，还是同一树枝上使用过呢？回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重为了理解去重我们来举一个例子，candidates = [1, 1, 2], target = 3，（方便起见candidates已经排序了）强调一下，树层去重的话，需要对数组排序！

选择过程树形结构如图所示：
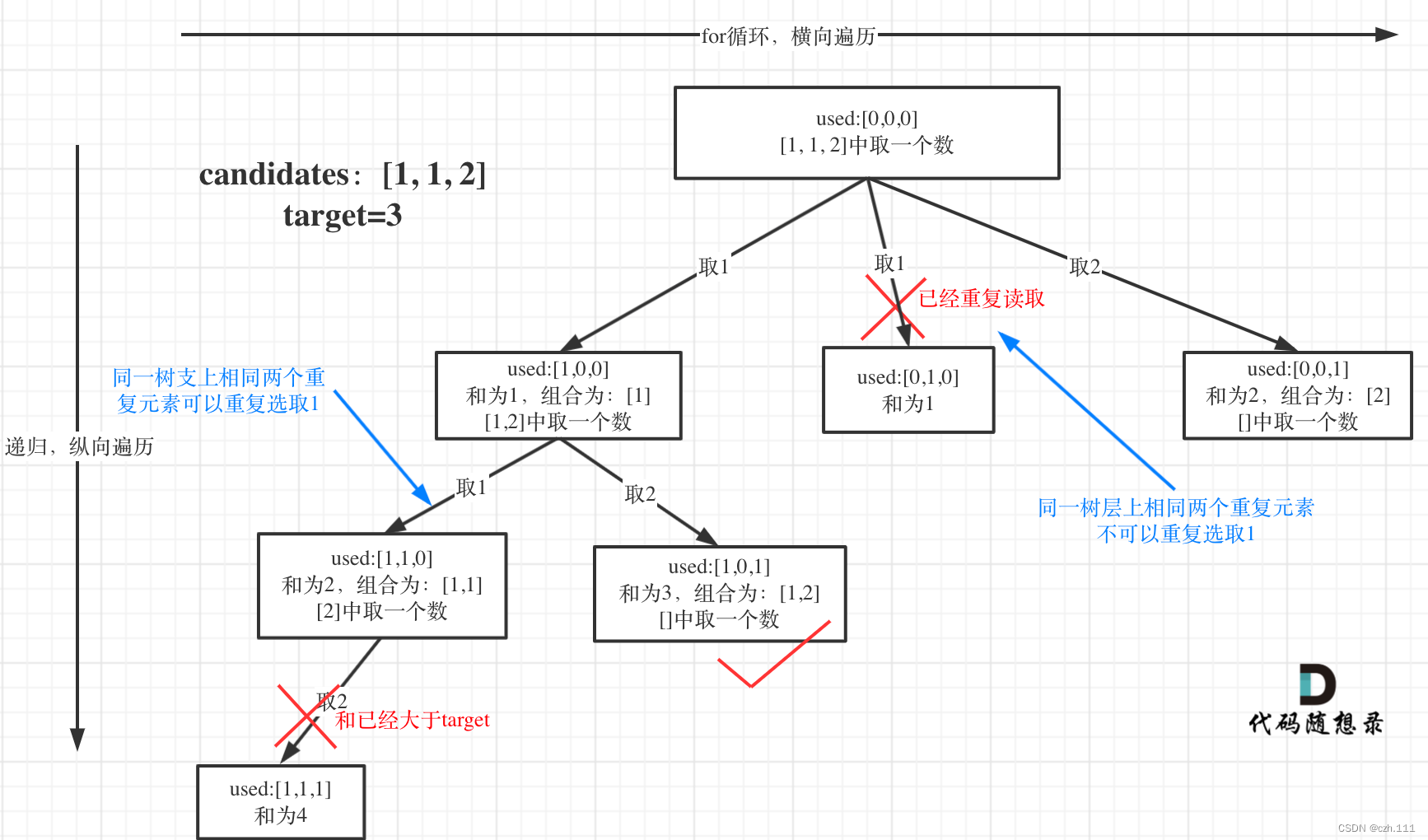
在这里插入图片描述

2.3附加代码如下所示：

//法1
class Solution {
public:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>&candidates,int target,int sum,int startindex,vector<bool>&used){if(sum>target)return;if(sum==target){result.push_back(path);return;}for(int i=startindex;i<candidates.size();i++){// used[i - 1] == true，说明同一树枝candidates[i - 1]使用过// used[i - 1] == false，说明同一树层candidates[i - 1]使用过// 要对同一树层使用过的元素进行跳过if(i>0&&candidates[i-1]==candidates[i]&&used[i-1]==false){continue;}path.push_back(candidates[i]);sum+=candidates[i];used[i]=true;backtracking(candidates,target,sum,i+1,used);//由于元素可重复 所以startindex要从i开始;// 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次path.pop_back();//回溯sum-=candidates[i];//回溯used[i]=false;}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool>used(candidates.size(),false);path.clear();result.clear();sort(candidates.begin(),candidates.end());// 首先把给candidates排序，让其相同的元素都挨在一起。backtracking(candidates,target,0,0,used);return result;}
};

//法2 直接采用startindex作为去重，不用used数组了
class Solution {
public:vector<vector<int>>result;vector<int>path;void backtracking(vector<int>&candidates,int target,int sum,int startindex){if(sum>target)return;if(sum==target){result.push_back(path);return;}for(int i=startindex;i<candidates.size();i++){//遍历下一个树层的时候只要前面有和当前遍历的元素数值相等就跳过if(i>startindex&&candidates[i-1]==candidates[i]){continue;}path.push_back(candidates[i]);sum+=candidates[i];backtracking(candidates,target,sum,i+1);//由于元素可重复 所以startindex要从i开始;// 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次path.pop_back();//回溯sum-=candidates[i];//回溯}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {path.clear();result.clear();sort(candidates.begin(),candidates.end());// 首先把给candidates排序，让其相同的元素都挨在一起。backtracking(candidates,target,0,0);return result;}
};

3.LeetCode.两个数组的交集

3.1题目链接：131.分割回文串

文章讲解：代码随想录
视频讲解：B站卡哥视频

3.2思路：

我们来分析一下切割，其实切割问题类似组合问题。
例如对于字符串abcdef：
组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…。
切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…。
所以切割问题，也可以抽象为一棵树形结构，如图：
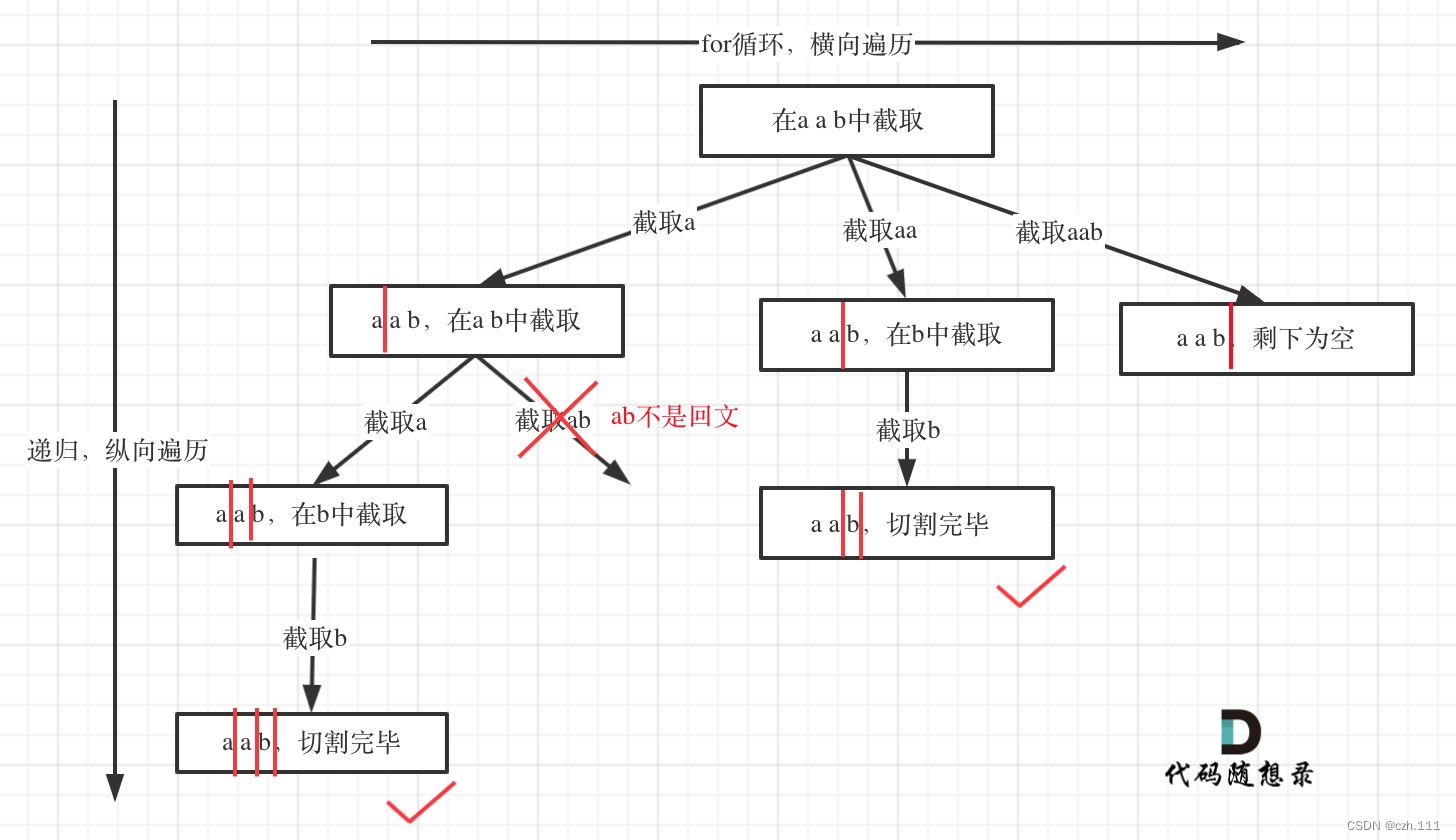在这里插入图片描述递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。此时可以发现，切割问题的回溯搜索的过程和组合问题的回溯搜索的过程是差不多的。

3.3附加代码如下所示：

class Solution {
public:vector<vector<string>>result;vector<string>path;// 放已经回文的子串void backtracking(const string &s,int startindex){// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if(startindex>=s.size()){result.push_back(path);return;}for(int i=startindex;i<s.size();i++){if(isPalindrome(s,startindex,i)){// 获取[startIndex,i]在s中的子串string str=s.substr(startindex,i-startindex+1);path.push_back(str);}else {continue;}backtracking(s,i+1); // 寻找i+1为起始位置的子串path.pop_back();// 回溯过程，弹出本次已经添加的子串}}bool isPalindrome(const string&s,int begin,int end){for( int i=begin,j=end;i<j;i++,j--){if(s[i]!=s[j])return false;}return true;}vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s,0);return result;}
};