本篇主要是对常见排序的分类和一些排序的详解

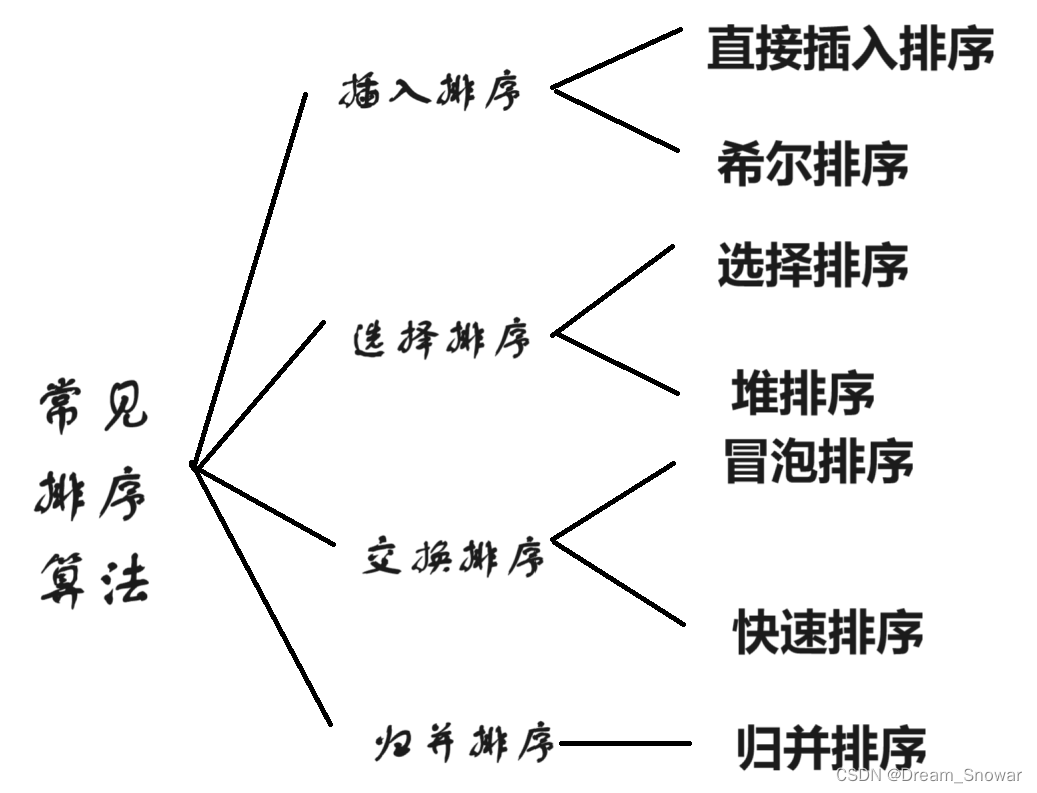
一、插入排序

1.直接插入排序

// 直接插入排序函数
void insertionSort(int arr[], int n) {int i, key, j;for (i = 1; i < n; i++) {key = arr[i]; // 取出待排序的元素j = i - 1;// 将大于key的元素向后移动一位while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j = j - 1;}arr[j + 1] = key; // 将key插入到正确的位置}
}

这个排序的时间复杂度为O（n^2）空间复杂度为O（1）

2.希尔排序

#include <stdio.h>
// 希尔排序函数，接受一个整数数组和数组长度作为参数
void shell_sort(int arr[], int n) 
{// 外层循环控制不同的间隔值gapfor (int gap = n / 3 + 1; gap > 0; gap /= 3) {// 内层循环遍历数组中的元素，从索引gap开始到数组末尾for (int i = gap; i < n; i++) {int temp = arr[i]; // 保存当前元素的值int j;// 比较当前元素与间隔为gap的前一个元素的大小，如果前一个元素较大，则交换它们的位置for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp; // 将保存的当前元素值赋给正确的位置}}
}

这个排序上回我们讲过了，空间复杂度为O(1)，时间复杂度为O（n^1.3）。

二、选择排序

1.选择排序

// 选择排序函数
void selectionSort(int arr[], int n) {int i, j, minIndex, temp;for (i = 0; i < n - 1; i++) {minIndex = i; // 记录当前最小值的索引for (j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j; // 更新最小值索引}}// 交换当前元素与最小值元素temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;}
}

这个排序的思路也很简单，时间复杂度为O(N^2),空间复杂度是O(1)

2.堆排序

// 调整堆
void adjustHeap(int arr[], int i, int length) {int temp = arr[i]; // 取出当前元素for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {if (k + 1 < length && arr[k] < arr[k + 1]) { // 如果右子节点大于左子节点，k指向右子节点k++;}if (arr[k] > temp) { // 如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）arr[i] = arr[k];i = k;} else {break;}}arr[i] = temp; // 将temp值放到最终的位置
}// 堆排序
void heapSort(int arr[], int length) {// 1.构建大顶堆for (int i = length / 2 - 1; i >= 0; i--) {adjustHeap(arr, i, length);}// 2.调整堆结构+交换堆顶元素与末尾元素for (int j = length - 1; j > 0; j--) {// 交换堆顶元素和末尾元素int temp = arr[j];arr[j] = arr[0];arr[0] = temp;// 重新对堆进行调整adjustHeap(arr, 0, j);}
}

堆排序的时间复杂度O(N*logN),空间复杂度O(1)

三、交换排序

1,冒泡排序

// 冒泡排序函数
void bubble_sort(int arr[], int n) {for (int i = 0; i < n - 1; i++) { // 外层循环控制排序趟数for (int j = 0; j < n - 1 - i; j++) { // 内层循环控制每趟比较的次数if (arr[j] > arr[j + 1]) { // 如果前一个元素大于后一个元素，交换它们的位置int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}

这个排序大家肯定都非常熟悉了,时间复杂度是O(n^2),空间复杂度是O(1)

2.快速排序

这个排序我们没讲过这里我们来讲一讲。

快速排序的整体思路就是保证基准值的左边的数小于基准值，右边大于基准值。

首先我们拥有如下数组

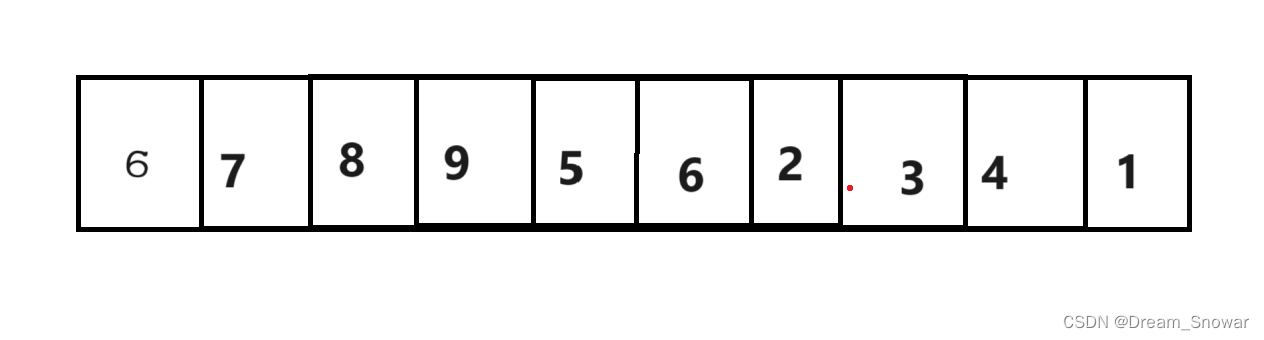
我们先选定一个基准值,(这里我们讲最基础的)我们选择第一个数作为基准值。

然后我们先从右往左走找小于基准值的值

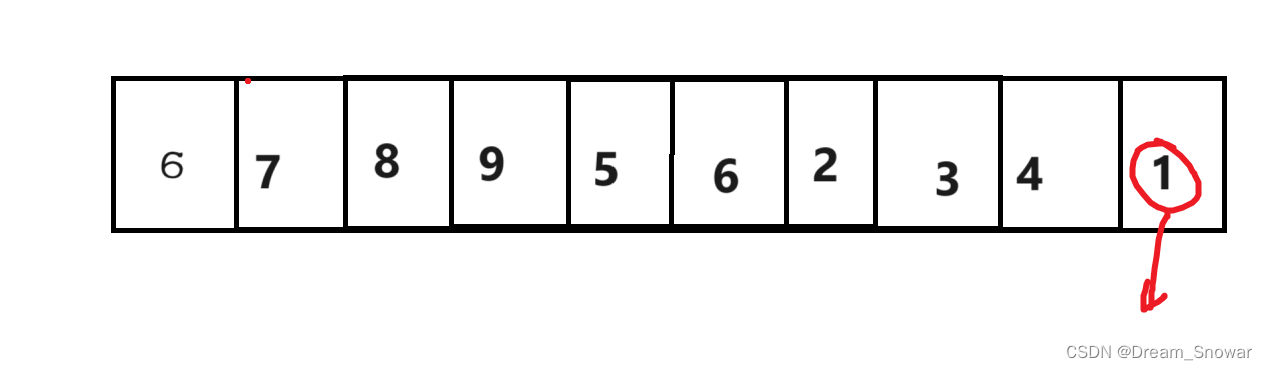
找到后我们从左往右找大于基准值的

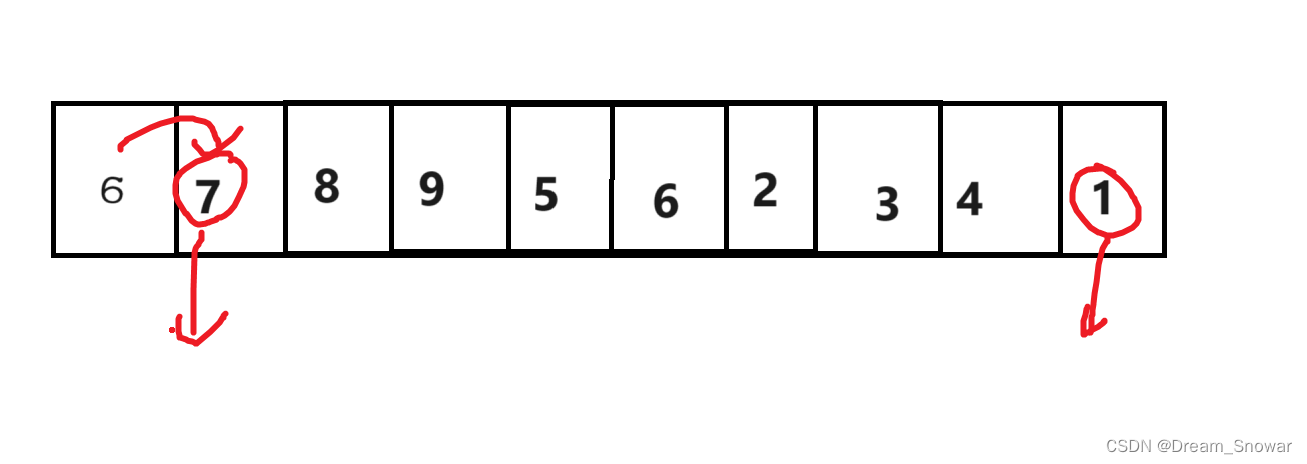
然后交换两个值

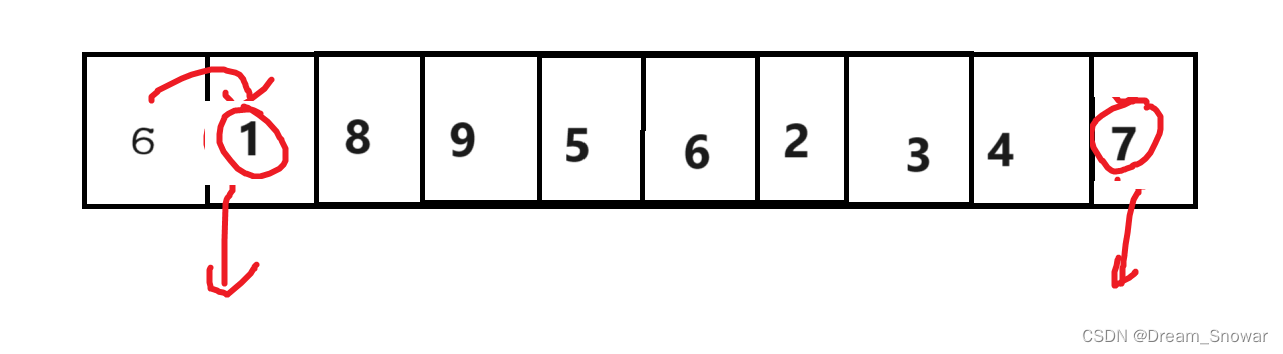
接着我们再重复之前的操作，直到相遇

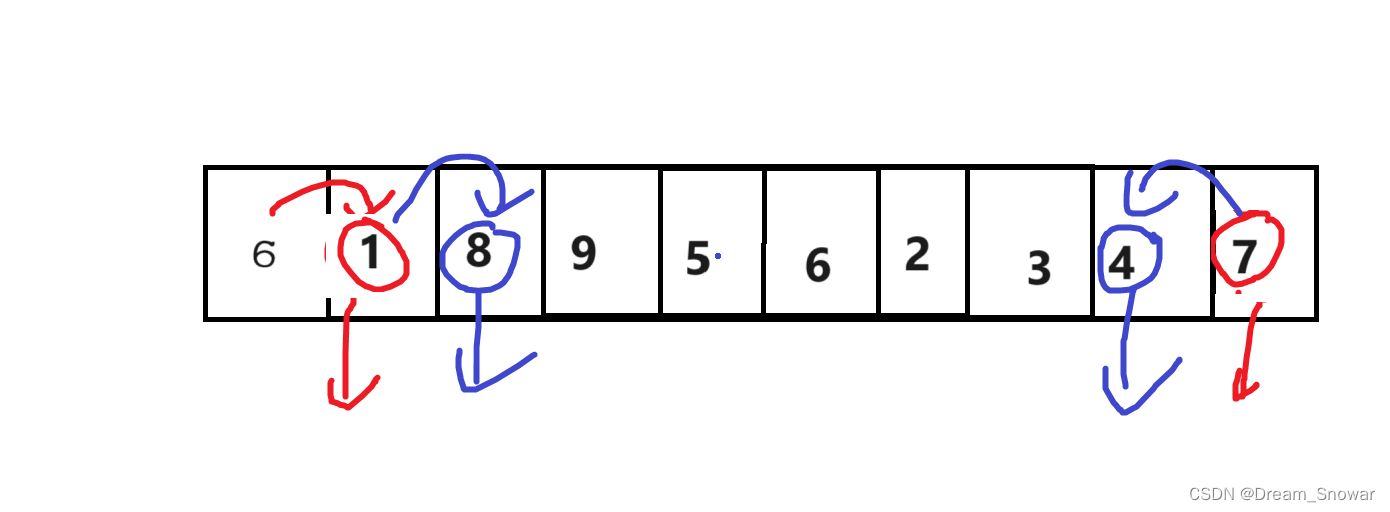
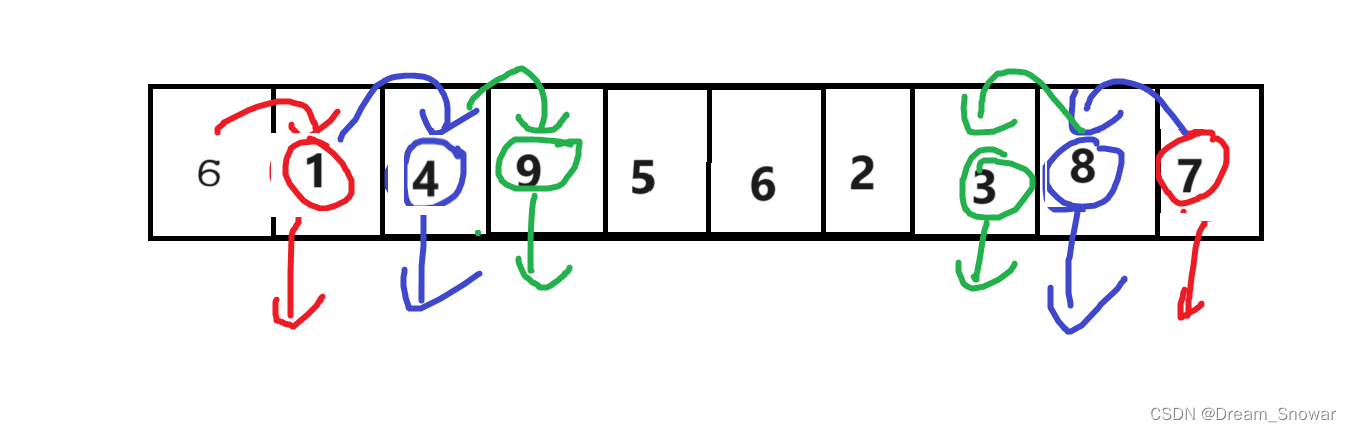
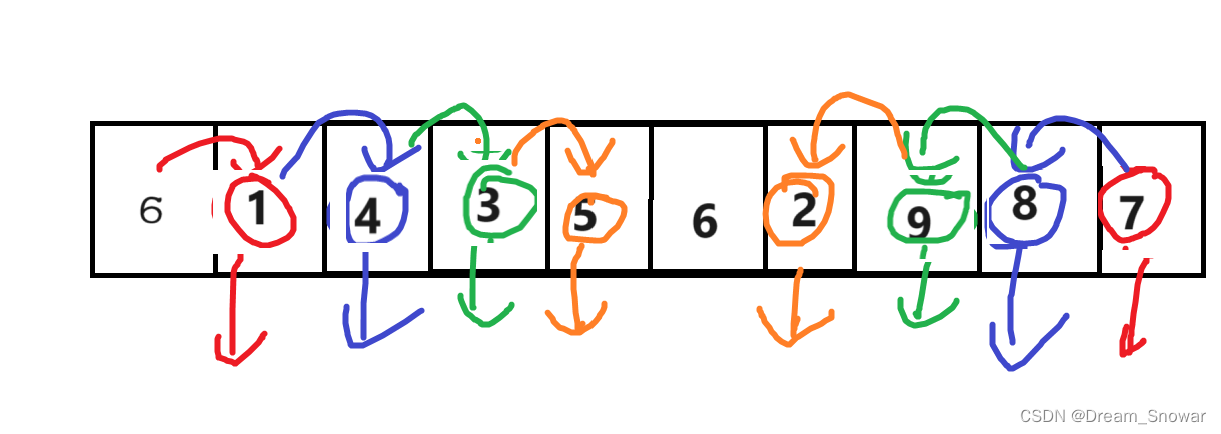
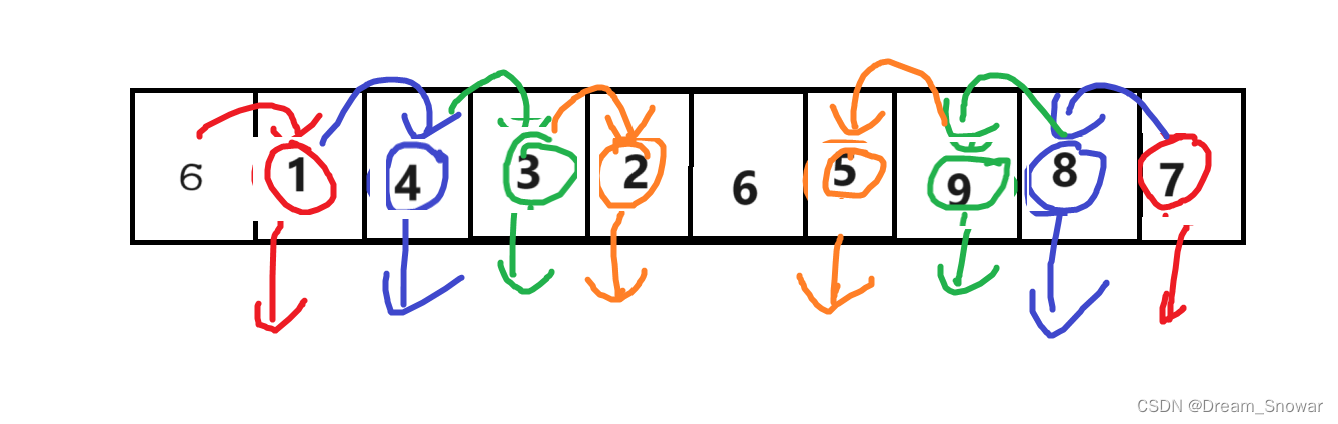
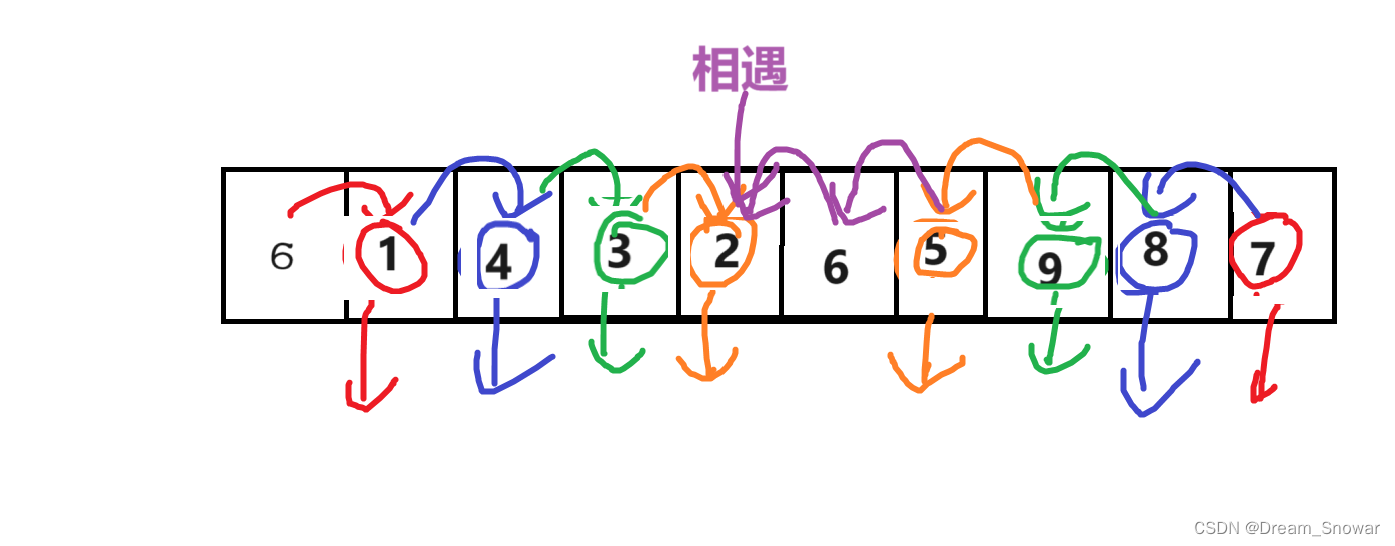
然后将相遇点和基准值交换

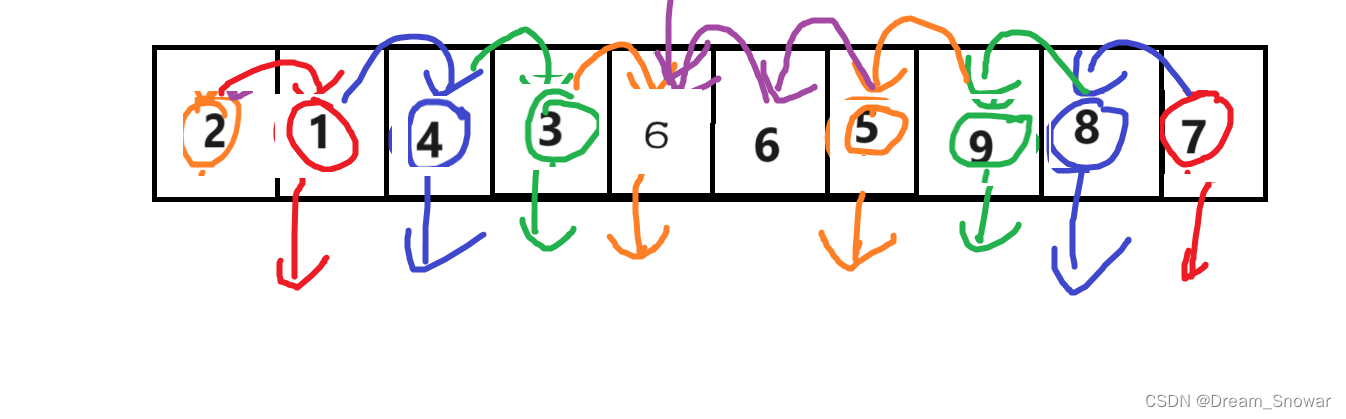
然后我们可以得到基准值的下标,然后最左端不变,以基准值的下标-1为最右端,以基准值的下标为最左端,最右端不变把原来的数据一分为二:

然后再分别进行快速排序,以此类推,直到所有递归都返回.

代码示例:

void QuickSort(int* a, int left, int right)
{// 区间只有一个值或者不存在就是最小子问题if (left >= right)return;int begin = left, end = right;int keyi = left;while (left < right){// right先走，找小while (left < right && a[right] >= a[keyi]){--right;}// left再走，找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1]keyi[keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

快速排序的空间复杂度O(logN)时间复杂度是O(N*logN)。有意思的是其实快速排序的时间复杂度不是最坏情况，最坏情况应该是O(N^2),但是出现的概率很小。其次我们可以通过各种方法来改进

举几个例子，就不展开讲了：

//三数取中
int GetMidi(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}

我们通过三数取中得到key

在快排开头加上这个，就可以很好的减少我们出现最坏情况

int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);

如果觉得三数取中比较复杂，我们可以去随机数作为key,虽然效率不高，但是写起来方便，也能减少出现最坏情况

int randi = rand() % (right - left + 1);
randi += left;
Swap(&a[left], &a[randi]);

快速排序其实分好几种，这里我再展示一种前后指针法，个人感觉写起来来简单一点

void QuickSort2(int* a, int left, int right)
{if (left >= right)return;int keyi = left;int prev = left;int cur = left+1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort2(a, left, keyi - 1);QuickSort2(a, keyi + 1, right);
}

这里再展示一下非递归的快速排序，感兴趣的可以自己看下（注意要结合栈）

void QuickSortNonR(int* a, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (StackEmpty(&st) != 0)
{right = StackTop(&st);StackPop(&st);left = StackTop(&st);StackPop(&st);if(right - left <= 1)continue;int div = PartSort1(a, left, right);// 以基准值为分割点，形成左右两部分：[left, div) 和 [div+1, right)StackPush(&st, div+1);StackPush(&st, right);StackPush(&st, left);StackPush(&st, div);
}StackDestroy(&s);
}

四、归并排序

归并排序（ MERGE-SORT ）是建立在归并操作上的一种有效的排序算法 ,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有 序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin == end)return;int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);// 归并int begin1 = begin,end1 = mid;int begin2 = mid + 1,end2 = end;int i = begin;// 依次比较，取小的尾插tmp数组while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a+begin, tmp + begin, sizeof(int) * (end - begin + 1));
}

void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n-1, tmp);free(tmp);tmp = NULL;
}

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int j = 0; j < n; j += 2 * gap){int begin1 = j, end1 = begin1 + gap - 1;int begin2 = begin1 + gap, end2 = begin2 + gap - 1;if (end1 >= n || begin2 >= n)break;if (end2 >= n)end2 = n - 1;int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + j, tmp + j, sizeof(int) * (end2-j+1));}gap *= 2;}free(tmp);tmp = NULL;
}