DAY17 平衡二叉树二叉树所有路径左叶子之和

12.平衡二叉树

给定一个二叉树，判断它是否是 平衡二叉树?

平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

示例 1：

img

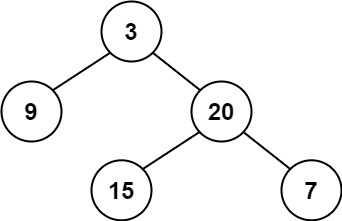
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

img

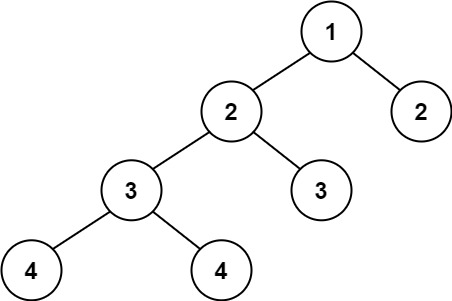
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

这里强调一波概念：

  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。
  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但leetcode中强调的深度和高度很明显是按照节点来计算的，如图：

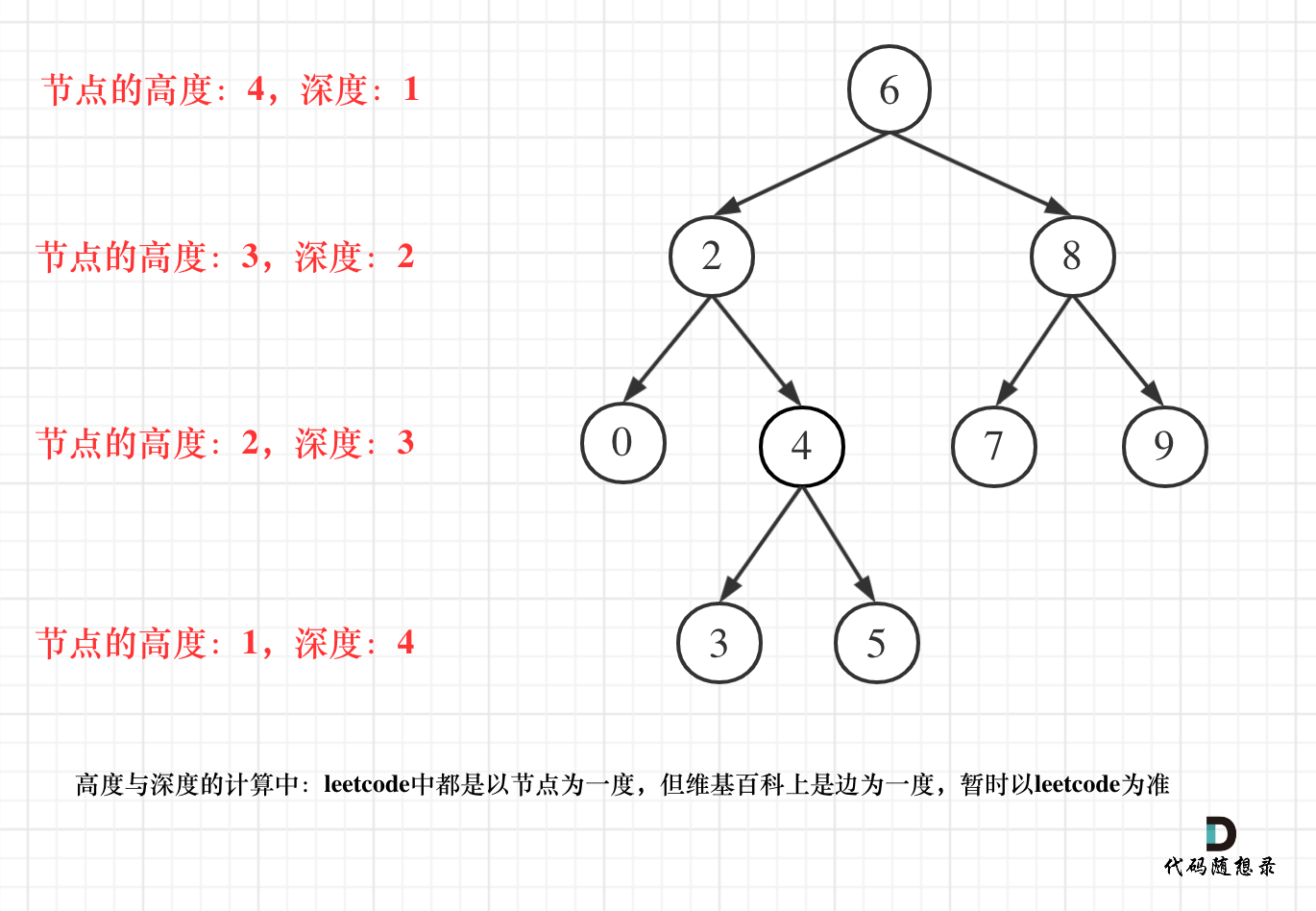
110.平衡二叉树2

关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准（毕竟要在这上面刷题）。

因为求深度可以从上到下去查 所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）

为什么二叉树的最大深度也用的后序遍历？

因为代码的逻辑其实是求的根节点的高度，而根节点的高度就是这棵树的最大深度，所以才可以使用后序遍历。

递归

既然要求比较高度，必然是要后序遍历。

  1. 明确递归函数的参数和返回值

参数：当前传入节点。 返回值：以当前传入节点为根节点的树的高度。

那么如何标记左右子树是否差值大于1呢？

如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。

// -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度
int getHeight(TreeNode* node)

2.明确终止条件

递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的树高度为0。

if (node == NULL) {return 0;
}

3.明确单层递归的逻辑

如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢？当然是其左子树高度和其右子树高度的差值。

分别求出其左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则返回-1，表示已经不是二叉平衡树了。

int leftHeight = getHeight(node->left); // 左
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // 右
if (rightHeight == -1) return -1;int result;
if (abs(leftHeight - rightHeight) > 1) {  // 中result = -1;
} else {result = 1 + max(leftHeight, rightHeight); // 以当前节点为根节点的树的最大高度
}return result;
//return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);//精简后

class Solution {
public:// 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1int getHeight(TreeNode* node) {if (node == NULL) {return 0;//表示当前节点为根节点的树高度为0}int leftHeight = getHeight(node->left);if (leftHeight == -1) return -1;int rightHeight = getHeight(node->right);if (rightHeight == -1) return -1;return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);}bool isBalanced(TreeNode* root) {return getHeight(root) == -1 ? false : true;}
};

迭代

在二叉树最大深度中，可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。

本题的迭代方式可以先定义一个函数，专门用来求高度。

这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）

【没理解！】

// cur节点的最大深度，就是cur的高度
int getDepth(TreeNode* cur){stack<TreeNode> st;if(st != NULL) st.push(cur);int depth = 0;//记录深度int result = 0;while(!st.empty()){TreeNode* node = st.top();if(node != NULL){st.push(node);//中st.push(NULL);depth++;if(node->right) st.push(node->right);//右  （空节点不入栈）if(node->left) st.push(node->left);//左    （空节点不入栈）}else{st.pop();//移除NULL标志值，当遇到一个NULL值时，说明当前节点的子节点已经被完全访问过了，所以需要将其从栈中移除。node = st.top();//第二次st.pop()操作是为了移除当前节点st.pop();depth--;}result = result > depth ? reuslt : depth;//更新返回值}return result;    
}

然后再用栈来模拟后序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合，代码如下：

bool isBalanced(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return true;st.push(root);while (!st.empty()) {TreeNode* node = st.top();                       // 中st.pop();if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { // 判断左右孩子高度是否符合return false;}if (node->right) st.push(node->right);           // 右（空节点不入栈）if (node->left) st.push(node->left);             // 左（空节点不入栈）}return true;
}

当然此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。

虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。

例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！

因为对于回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。

总结

1.求二叉树深度 和 二叉树高度的差异，求深度适合用前序遍历，而求高度适合用后序遍历。

2.迭代法没太理解：

​ 通过栈模拟的后序遍历找每一个节点的高度？

3.递归法：对于空节点返回0；对于高度差超过1返回-1；否则就返回当前节点的最大高度。最后判断返回根节点的值是-1，还是最大高度，进行判断true或false。

13.二叉树所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

img

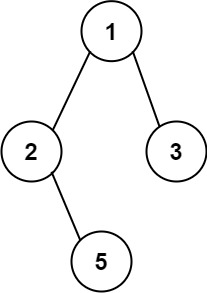
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

思路

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：

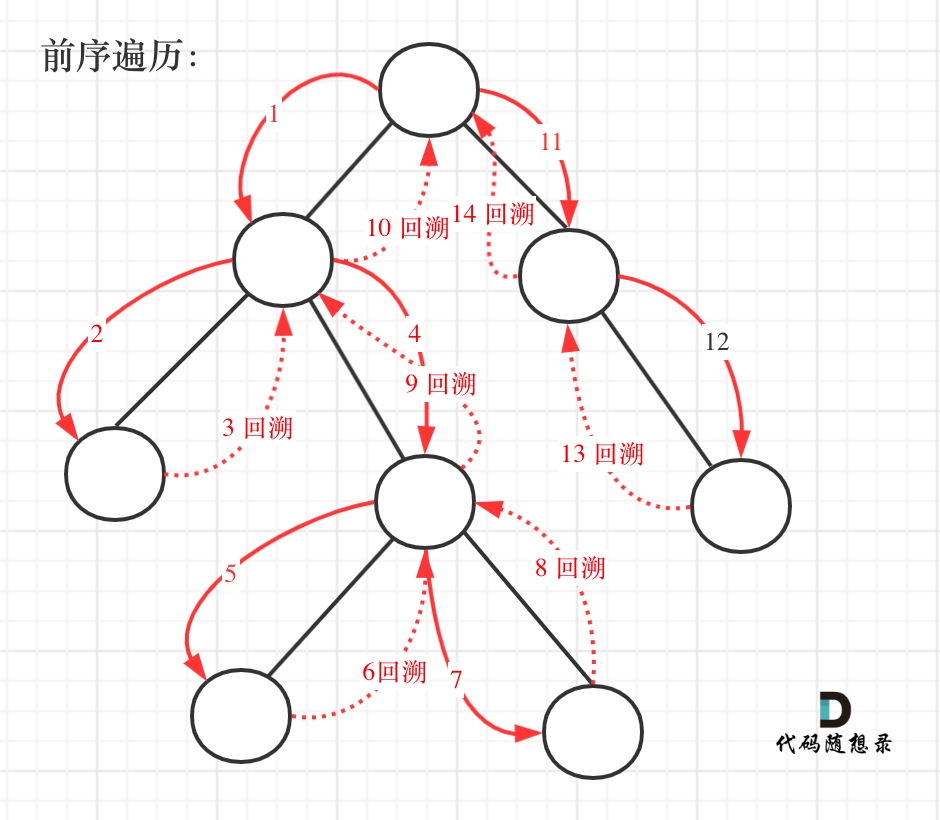
257.二叉树的所有路径

我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯

递归

  1. 递归函数参数以及返回值

要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值，代码如下：

void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)

​ 2.确定递归终止条件

在写递归的时候都习惯了这么写：

if (cur == NULL) {终止处理逻辑
}

但是本题的终止条件这样写会很麻烦，因为本题要找到叶子节点，就开始结束的处理逻辑了（把路径path放进result里）。

那么什么时候算是找到了叶子节点？ 是当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。

所以本题的终止条件是：

if (cur->left == NULL && cur->right == NULL) {终止处理逻辑
}

为什么没有判断cur是否为空呢？因为下面的逻辑可以控制空节点不入循环。

再来看一下终止处理的逻辑。

这里使用vector 结构path来记录路径，所以要把vector 结构的path转为string格式，再把这个string 放进 result里。

那么为什么使用了vector 结构来记录路径呢？ 因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。

有些人的代码也没有回溯，其实是有回溯的，只不过隐藏在函数调用时的参数赋值里

if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点string sPath;//声明一个空字符for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]); // 记录最后一个节点（叶子节点）result.push_back(sPath); // 收集一个路径return;
}

​ 3.确定单层递归逻辑

因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。

path.push_back(cur->val);

然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。

所以递归前要加上判断语句，下面要递归的节点是否为空，如下

if (cur->left) {traversal(cur->left, path, result);
}
if (cur->right) {traversal(cur->right, path, result);
}

此时还没完，递归完，要做回溯啊，因为path 不能一直加入节点，它还要删节点，然后才能加入新的节点。

那么回溯要怎么回溯呢，一些同学会这么写，如下：

if (cur->left) {traversal(cur->left, path, result);
}
if (cur->right) {traversal(cur->right, path, result);
}
path.pop_back();

这个回溯就有很大的问题，我们知道，回溯和递归是一一对应的，有一个递归，就要有一个回溯，这么写的话相当于把递归和回溯拆开了， 一个在花括号里，一个在花括号外。

所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！

那么代码应该这么写：

if (cur->left) {traversal(cur->left, path, result);path.pop_back(); // 回溯
}
if (cur->right) {traversal(cur->right, path, result);path.pop_back(); // 回溯
}
img

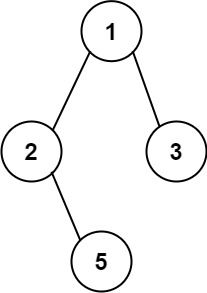
回溯的意思是：对于path：1 ， 2， 5；是一条路径了，那接下来要弹出5，2；再去添加 3，组成 1， 3这条新路径添加进result中。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void traversal(TreeNode* cur, vector<int>& path, vector<string>& result){path.push_back(cur->val);//中  中为什么写在这里，因为最后一个节点也要加入到path中 if(cur->left == nullptr && cur->right == nullptr){// 这才到了叶子节点string sPath;for(int i = 0; i < path.size() - 1; i++){sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size()-1]);result.push_back(sPath);//添加进结果中return;}if(cur->left){traversal(cur->left,path,result);//左path.pop_back();//去掉数组的最后一个数据}if(cur->right){traversal(cur->right,path,result);//右path.pop_back();//去掉数组的最后一个数据} }vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if(root == nullptr) return result;traversal(root,path,result);return result;}
};

精简代码：

class Solution {
private:void traversal(TreeNode* cur, string path, vector<string>& result) {//string path 每次都是复制赋值，不用使用引用path += to_string(cur->val); // 中if (cur->left == NULL && cur->right == NULL) {result.push_back(path);return;}//每次函数调用完，path依然是没有加上"->" 的，这就是回溯if (cur->left) traversal(cur->left, path + "->", result); // 左if (cur->right) traversal(cur->right, path + "->", result); // 右}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;string path;if (root == NULL) return result;traversal(root, path, result);return result;}
};

如上代码精简了不少，也隐藏了不少东西。

注意在函数定义的时候void traversal(TreeNode* cur, string path, vector<string>& result) ，定义的是string path，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。（这里涉及到C++语法知识）

那么在如上代码中，貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在traversal(cur->left, path + "->", result);中的 path + "->"。 每次函数调用完，path依然是没有加上"->" 的，这就是回溯了。

如果改写

if (cur->left) traversal(cur->left, path + "->", result); // 左  回溯就隐藏在这里

成为：

if (cur->left) {path += "->";traversal(cur->left, path, result); // 左
}
if (cur->right) {path += "->";traversal(cur->right, path, result); // 右
}

此时就没有回溯了，这个代码就是通过不了的了。

如果想把回溯加上，就要 在上面代码的基础上，加上回溯，就可以AC了。

if (cur->left) {path += "->";traversal(cur->left, path, result); // 左path.pop_back(); // 回溯 '>'path.pop_back(); // 回溯 '-'
}
if (cur->right) {path += "->";traversal(cur->right, path, result); // 右path.pop_back(); // 回溯 '>' path.pop_back(); //  回溯 '-' 
}

整体代码：

//版本二
class Solution {
private:void traversal(TreeNode* cur, string path, vector<string>& result) {path += to_string(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中if (cur->left == NULL && cur->right == NULL) {result.push_back(path);return;}if (cur->left) {path += "->";traversal(cur->left, path, result); // 左path.pop_back(); // 回溯 '>'path.pop_back(); // 回溯 '-'}if (cur->right) {path += "->";traversal(cur->right, path, result); // 右path.pop_back(); // 回溯'>'path.pop_back(); // 回溯 '-'}}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;string path;if (root == NULL) return result;traversal(root, path, result);return result;}
};

总结

1.**可以感受出来，如果把 path + "->"作为函数参数就是可以的，因为并没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）**在第一个版本中，函数参数我就使用了引用，即 vector<int>& path ，这是会拷贝地址的，所以 本层递归逻辑如果有path.push_back(cur->val); 就一定要有对应的 path.pop_back()

为什么不去定义一个 string& path 这样的函数参数呢？

path += to_string(cur->val); 每次是加上一个数字，这个数字如果是个位数，那好说，就调用一次path.pop_back()，但如果是 十位数，百位数，千位数呢？ 百位数就要调用三次path.pop_back()，才能实现对应的回溯操作，这样代码实现就太冗余了。

所以才使用 vector 类型的path，这样方便给大家演示代码中回溯的操作。 vector类型的path，不管 每次 路径收集的数字是几位数，总之一定是int，所以就一次 pop_back就可以。

2.第二种递归的代码（形参处做了隐形回溯）虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现出来了。所以这是参数中，不带引用，不做地址拷贝，只做内容拷贝的效果。

迭代法

除了模拟递归需要一个栈，同时还需要一个栈来存放对应的遍历路径。

class Solution {
public:vector<string> binaryTreePaths(TreeNode* root) {stack<TreeNode*> treeSt;// 保存树的遍历节点stack<string> pathSt;   // 保存遍历路径的节点vector<string> result;  // 保存最终路径集合if (root == NULL) return result;treeSt.push(root);pathSt.push(to_string(root->val));while (!treeSt.empty()) {TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径if (node->left == NULL && node->right == NULL) { // 遇到叶子节点result.push_back(path);}if (node->right) { // 右treeSt.push(node->right);pathSt.push(path + "->" + to_string(node->right->val));}if (node->left) { // 左treeSt.push(node->left);pathSt.push(path + "->" + to_string(node->left->val));}}return result;}
};

二叉树周总结

1.判断二叉树是否对称

本质是要比较两个树（这两个树是根节点的左右子树），遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

而本题的迭代法中我们使用了队列，需要注意的是这不是层序遍历，而且仅仅通过一个容器来成对的存放我们要比较的元素，认识到这一点之后就发现：用队列，用栈，甚至用数组，都是可以的。

2.树的最大深度

本题可以使用前序，也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序呢求的是高度。

而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

使用前序(充分表现出求深度回溯的过程)

3.树的最小深度

注意这里最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点！

求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

4.求二叉树的节点数量

5.判断二叉树是否是平衡二叉树

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。

二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。

但leetcode中强调的深度和高度很明显是按照节点来计算的。

回溯法其实就是递归

讲了这么多二叉树题目的迭代法，有的同学会疑惑，迭代法中究竟什么时候用队列，什么时候用栈？

如果是模拟前中后序遍历就用栈，如果是适合层序遍历就用队列，当然还是其他情况，那么就是 先用队列试试行不行，不行就用栈。

6.二叉树所有路径

其实回溯和递归都是相伴相生的

回溯就隐藏在traversal(cur->left, path + “->”, result);中的 path + “->”。 每次函数调用完，path依然是没有加上"->" 的，这就是回溯了

总结

二叉树的题目，都是使用了递归三部曲一步一步的把整个过程分析出来，而不是上来就给出简洁的代码。

15.左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

img

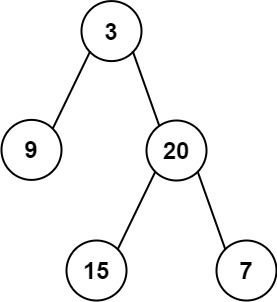
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

思路

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。

因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

大家思考一下如下图中二叉树，左叶子之和究竟是多少？

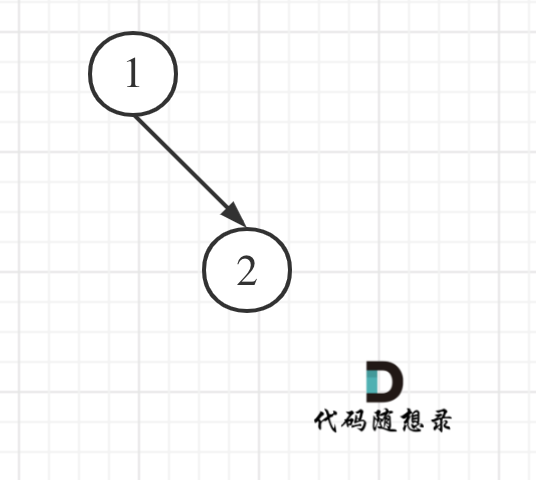
404.左叶子之和

其实是0，因为这棵树根本没有左叶子！

图二

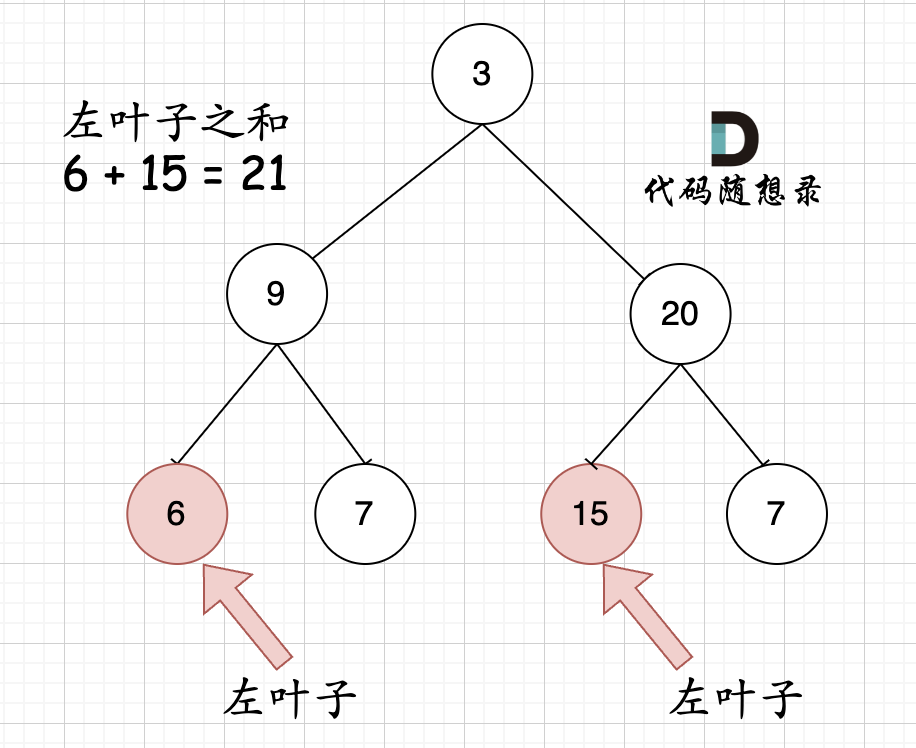
那么判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。

如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下：

if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {左叶子节点处理逻辑
}

递归法

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

  1. 确定递归函数的参数和返回值

判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int。

​ 2.确定终止条件

如果遍历到空节点，那么左叶子值一定是0

if (root == NULL) return 0;

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：

if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写，如果不写不影响结果，但就会让递归多进

​ 3.确定单层递归的逻辑

当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

int leftValue = sumOfLeftLeaves(root->left);    // 左
if (root->left && !root->left->left && !root->left->right) {leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right);  // 右int sum = leftValue + rightValue;               // 中
return sum;

整体代码：

class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left);    // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;//左子叶的处理逻辑不太理解}int rightValue = sumOfLeftLeaves(root->right);  // 右int sum = leftValue + rightValue;               // 中return sum;}
};

迭代法

本题迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了。

前序遍历：

class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return 0;st.push(root);int result = 0;while (!st.empty()) {TreeNode* node = st.top();st.pop();if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {result += node->left->val;}if (node->right) st.push(node->right);if (node->left) st.push(node->left);}return result;}
};

总结

这道题目要求左叶子之和，其实是比较绕的，因为不能判断本节点是不是左叶子节点。

**什么是左叶子节点？**首先要是叶子节点，其次叶子节点是左节点。

此时就要通过节点的父节点来判断其左孩子是不是左叶子了。

平时我们解二叉树的题目时，已经习惯了通过节点的左右孩子判断本节点的属性，而本题我们要通过节点的父节点判断本节点的属性。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/295555.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

ZKP价值链路的垂直整合

ZKP价值链路的垂直整合

1. ZKP proof生命周期 从ZKP&#xff08;zero-knowledge proof&#xff09;生命周期&#xff0c;先看围绕ZKP的价值链路形成&#xff1a; 1&#xff09;User intent用户意图&#xff1a;以某用户意图为起点&#xff0c;如想要在某zk-rollup上swap某token、证明其身份、执行某…
阅读更多...
EasyExcel 模板导出excel、合并单元格及单元格样式设置。 Freemarker导出word 合并单元格

EasyExcel 模板导出excel、合并单元格及单元格样式设置。 Freemarker导出word 合并单元格

xls文件&#xff1a; 后端代码&#xff1a; InputStream filePath this.getClass().getClassLoader().getResourceAsStream(templateFile);// 根据模板文件生成目标文件ExcelWriter excelWriter EasyExcel.write(orgInfo.getFilename()).excelType(ExcelTypeEnum.XLS).withTe…
阅读更多...
element-ui badge 组件源码分享

element-ui badge 组件源码分享

今日简单分享 badge 组件的源码实现&#xff0c;主要从以下两个方面&#xff1a; 1、badge 组件页面结构 2、badge 组件属性 一、badge 组件页面结构 二、badge 组件属性 补充几个标签的用途&#xff1a; sub&#xff1a;下标、sup&#xff1a;上标、var 变量 代码如下&am…
阅读更多...
docker搭建CI/CD环境配置过程中的常见问题

docker搭建CI/CD环境配置过程中的常见问题

一、Jenkins 1、pull镜像问题 docker pull jenkins/jenkins:lts Using default tag: latest Trying to pull repository docker.io/library/centos ... Get https://registry-1.docker.io/v2/library/centos/manifests/latest: Get https://auth.docker.io/token?scoperepo…
阅读更多...
端点攻击剖析：网络攻击如何破坏企业网络

端点攻击剖析：网络攻击如何破坏企业网络

为了实现真正有效的网络安全态势&#xff0c;将公司的所有设备作为网络设备进行保护至关重要。攻击者可以将任何端点&#xff08;电话、计算机、虚拟机、嵌入式设备、服务器、POS 终端&#xff09;变成进入组织的入口点。 未受保护的端点是恶意行为者的主要攻击媒介&#xff0…
阅读更多...
Git 核心知识

Git 核心知识

2024年4月2日更新 Git 安装 官网下载&#xff0c;Git 选择合适的版本&#xff0c;无脑下一步即可。 安装成功之后&#xff0c;鼠标右键任意的文件夹&#xff0c;会出现 Git GUI 的选项&#xff0c;即安装成功 安装注意事项 安装前&#xff0c;检查环境变量 &#xff0c; 如…
阅读更多...
15.Python访问数据库

15.Python访问数据库

如果数据量较少&#xff0c;则我们可以将数据保存到文件中&#xff1b;如果数据量较 大&#xff0c;则我们可以将数据保存到数据库中。 1 SQLite数据库 SQLite是嵌入式系统使用的关系数据库&#xff0c;目前的主流版本是SQLite 3。SQLite是开源的&#xff0c;采用C语言编写而…
阅读更多...
Springboot整合Milvus向量库

Springboot整合Milvus向量库

1. Milvus的Maven依赖&#xff0c; 配置如下 <dependency><groupId>io.milvus</groupId><artifactId>milvus-sdk-java</artifactId><version>2.3.4</version><exclusions><exclusion><artifactId>log4j-slf4j-imp…
阅读更多...
组合总和-java

组合总和-java

题目描述: 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target &#xff0c;找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 &#xff0c;并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重复被…
阅读更多...
HTML常用的图片标签和超链接标签

HTML常用的图片标签和超链接标签

目录 一.常用的图片标签和超链接标签&#xff1a; 1.超链接标签&#xff1a; 前言: 超链接的使用&#xff1a; target属性: 1)鼠标样式&#xff1a; 2)颜色及下划线: 总结: 2.图片标签&#xff1a; 前言: img的使用: 设置图片&#xff1a; 1.设置宽度和高度: 2.HTM…
阅读更多...
C++心决之内联函数+auto关键字+指针空值

C++心决之内联函数+auto关键字+指针空值

目录 7.内联函数 7.1 概念 7.2 特性 8. auto关键字(C11) 8.1 类型别名思考 8.2 auto简介 8.3 auto的使用细则 8.4 auto不能推导的场景 9. 基于范围的for循环(C11) 9.1 范围for的语法 9.2 范围for的使用条件 10. 指针空值nullptr(C11) 10.1 C98中的指针空值 7.内联…
阅读更多...
R语言颜色细分

R语言颜色细分

1.如何对R语言中两种颜色之间进行细分 2.代码&#xff1a; x <- colorRampPalette(c("#FC8D62","#FDEAE6"))(12) #打印向量值 # 按字典顺序排序颜色值 x_sorted <- sort(x,decreasing TRUE)# 打印排序后的颜色值 print(x_sorted)#展示颜色 scales:…
阅读更多...
18.web 应用测试

18.web 应用测试

每年必考&#xff1b; 考几个关键点&#xff1a; 1、计算通信量&#xff1b;给定并发多少、每个并发事务请求的量是多少、单位时间并发有多少个请求&#xff1b;计算吞吐量&#xff1b; 解&#xff1a;记公式&#xff1b;课上不讲&#xff0c;真题里有公式&#xff1b;比较容易…
阅读更多...
解决Flutter应用在苹果商店上架中常见的问题与挑战

解决Flutter应用在苹果商店上架中常见的问题与挑战

引言 Flutter是一款由Google推出的跨平台移动应用开发框架&#xff0c;其强大的性能和流畅的用户体验使其备受开发者青睐。然而&#xff0c;开发一款应用只是第一步&#xff0c;将其成功上架到苹果商店才是实现商业目标的关键一步。本文将详细介绍如何使用Flutter将应用程序上…
阅读更多...
第十四章 MySQL

第十四章 MySQL

一、MySQL 1.1 MySql 体系结构 MySQL 架构总共四层&#xff0c;在上图中以虚线作为划分。 1. 最上层的服务并不是 MySQL 独有的&#xff0c;大多数给予网络的客户端/服务器的工具或者服务都有类似的架构。比如&#xff1a;连接处理、授权认证、安全等。 2. 第二层的架构包括…
阅读更多...
JWFD流程图转换为矩阵数据库的过程说明

JWFD流程图转换为矩阵数据库的过程说明

在最开始设计流程图的时候&#xff0c;请务必先把开始节点和结束节点画到流程图上面&#xff0c;就是设计器面板的最开始两个按钮&#xff0c;先画开始点和结束点&#xff0c;再画中间的流程&#xff0c;然后保存&#xff0c;这样提交到矩阵数据库就不会出任何问题&#xff0c;…
阅读更多...
MQ消息队列详解以及MQ重复消费问题

MQ消息队列详解以及MQ重复消费问题

MQ消息队列详解以及MQ重复消费问题 1、解耦2、异步调用3、流量削峰4、MQ重复消费问题&#xff0c;以及怎么解决&#xff1f;4.1、重复消费产生4.2、解决方法&#xff1a; https://blog.csdn.net/qq_44240587/article/details/104630567 核心的就是&#xff1a;解耦、异步、削锋…
阅读更多...
C#/WPF 使用开源Wav2Lip做自己的数字人(无需安装环境)

C#/WPF 使用开源Wav2Lip做自己的数字人(无需安装环境)

实现效果 Speaker Wav2Lip概述 2020年&#xff0c;来自印度海德拉巴大学和英国巴斯大学的团队&#xff0c;在ACM MM2020发表了的一篇论文《A Lip Sync Expert Is All You Need for Speech to Lip Generation In The Wild 》&#xff0c;在文章中&#xff0c;他们提出一个叫做Wa…
阅读更多...
【R】Error in library(foreach) : 不存在叫‘foreach’这个名字的程辑包

【R】Error in library(foreach) : 不存在叫‘foreach’这个名字的程辑包

Error in library(foreach) : 不存在叫‘foreach’这个名字的程辑包 此外: Warning message: package ‘parallel’ is a base package, and should not be updated 解决方法 缺少名为 foreach 的包&#xff0c;使用install.packages("foreach")将名为foreach 的包…
阅读更多...
人脸、指纹、刷卡、密码、远程，一文速懂不同功能门禁系统怎么选？

人脸、指纹、刷卡、密码、远程，一文速懂不同功能门禁系统怎么选？

门禁系统顾名思义就是对出入口通道进行管制的系统&#xff0c;它是在传统的门锁基础上发展而来。常见的门禁系统包括&#xff1a;密码识别门禁系统、刷卡识别门禁系统、生物识别门禁系统以及线上远程开门系统等。 在选择门禁系统时&#xff0c;需要根据不同的场景和需求&#x…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023