二叉搜索树
左子树的结点都比当前结点小,右子树的结点都比当前结点大。
构造二叉搜索树:
let arr = [3, 4, 7, 5, 2]function Node(value) {this.value = valuethis.left = nullthis.right = null
}/*** 添加结点* @param root 当前结点* @param num 新的结点的值*/
function addNode(root, num) {if (root == null) returnif (root.value == num) returnif (root.value < num) {if (root.right == null) root.right = new Node(num)else addNode(root.right, num)} else {if (root.left == null) root.left = new Node(num)else addNode(root.left, num)}
}function binarySearchTree(arr) {if (arr == null || arr.length == 0) return nulllet root = new Node(arr[0])for (let i = 1; i < arr.length; i++) {addNode(root, arr[i])}return root
}
let root = binarySearchTree(arr)
console.dir(root)
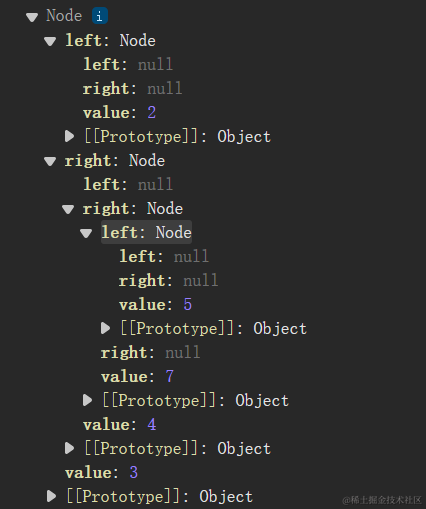
二叉搜索树的应用:
let arr = [3, 4, 7, 5, 2]function Node(value) {this.value = valuethis.left = nullthis.right = null
}/*** 添加结点* @param root 当前结点* @param num 新的结点的值*/
function addNode(root, num) {if (root == null) returnif (root.value == num) returnif (root.value < num) {if (root.right == null) root.right = new Node(num)else addNode(root.right, num)} else {if (root.left == null) root.left = new Node(num)else addNode(root.left, num)}
}function binarySearchTree(arr) {if (arr == null || arr.length == 0) return nulllet root = new Node(arr[0])for (let i = 1; i < arr.length; i++) {addNode(root, arr[i])}return root
}function searchByTree (root,target) {if (root == null) return falseif (root.value == target) return trueif (root.value > target) return searchByTree(root.left, target)else return searchByTree(root.right, target)
}let root = binarySearchTree(arr)
console.log(searchByTree(root, 4))
平衡二叉树
- 根节点的左子树和右子树的高度处不能超过1
- 每棵子树都符合上述规则
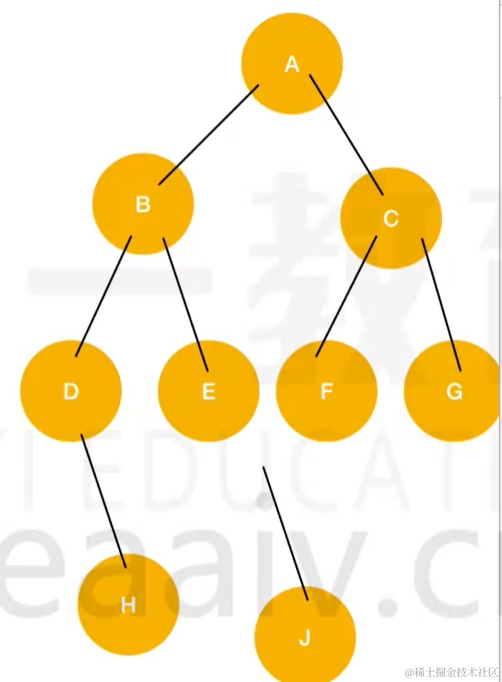
function Node(value) {this.value = valuethis.left = nullthis.right = null
}let a = new Node('a')
let b = new Node('b')
let c = new Node('c')
let d = new Node('d')
let e = new Node('e')
let f = new Node('f')
let g = new Node('g')
let h = new Node('h')
let j = new Node('j')
a.left = b
a.right = c
b.left = d
b.right = e
c.left = f
c.right = g
d.right = h
e.right = jfunction getDeep(root) {if (root == null) return 0let leftDeep = getDeep(root.left)let rightDeep = getDeep(root.right)return Math.max(leftDeep, rightDeep) + 1
}function isBalance(root) {if (root == null) return truelet leftDeep = getDeep(root.left)let rightDeep = getDeep(root.right)if (Math.abs(leftDeep - rightDeep) > 1) {return false} else {return isBalance(root.left) && isBalance(root.right)}
}console.log(getDeep(a))
console.log(isBalance(a))
单旋
某一节点不平衡,如果左边浅,右边深,进行左单旋。
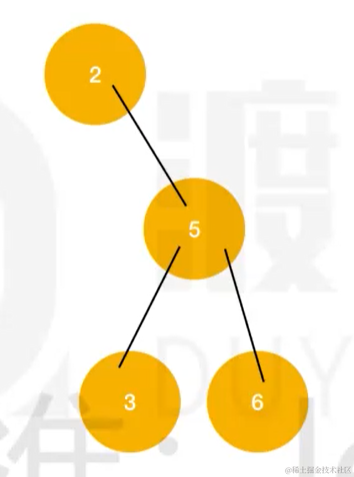
- 旋转节点:不平衡的节点为旋转节点(2)
- 新根:旋转之后称为根节点的节点(5)
- 变化分支:父级节点发生变化的那个分支
- 不变分支:父级节点不变的那个分支
左单旋时:
- 旋转节点:当前不平衡的节点 2
- 新根:右子树的根节点 5
- 变化分支:旋转节点的右子树的左子树 3
- 不变分支:旋转节点的右子树的右子树 6
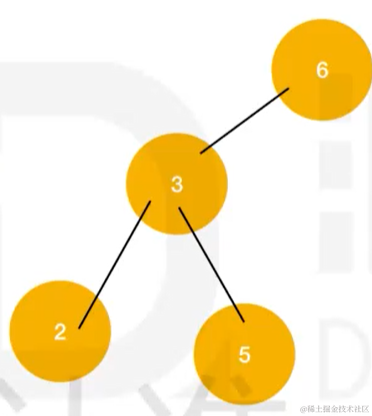
右单旋时:
- 旋转节点:当前不平衡的节点 6
- 新根:左子树的根节点 3
- 变化分支:旋转节点的左子树的右子树 5
- 不变分支:旋转节点的左子树的左子树 2
步骤:
- 进行左单旋
-
- 找到新根
-
- 找到变化分支
-
- 当前旋转节点的右孩子为变化分支
-
- 新根的左孩子为旋转节点
-
- 返回新的根节点
- 进行右单旋
-
- 找到新根
-
- 找到变化分支
-
- 当前旋转节点的左孩子为变化分支
-
- 新根的右孩子为旋转节点
-
- 返回新的根节点
function Node(value) {this.value = valuethis.left = nullthis.right = null
}let node2 = new Node('2')
let node5 = new Node('5')
let node3 = new Node('3')
let node6 = new Node('6')
node2.right= node5
node5.left = node3
node5.right = node6function getDeep(root) {if (root == null) return 0let leftDeep = getDeep(root.left)let rightDeep = getDeep(root.right)return Math.max(leftDeep, rightDeep) + 1
}function isBalance(root) {if (root == null) return truelet leftDeep = getDeep(root.left)let rightDeep = getDeep(root.right)if (Math.abs(leftDeep - rightDeep) > 1) {return false} else {return isBalance(root.left) && isBalance(root.right)}
}function leftRotate (root){// 找到新根let newRoot= root.right// 找到变化分支let changeBranch = root.right.left// 当前旋转接点的右节点变为变化分支root.right = changeBranch// 新根的左节点变为旋转分支newRoot.left = root// 返回新的根节点return newRoot
}
function rightRotate (root){let newRoot = root.leftlet changeBranch = root.left.rightroot.left = changeBranchnewRoot.right = rootreturn newRoot
}/*** 平衡二叉树* @param root 根节点* @returns {*|boolean} 平衡后的根节点*/
function change(root) {if (isBalance(root)) return rootif (root.left != null) root.left = change(root.left)if (root.right != null) root.right = change(root.right)let leftDeep = getDeep(root.left)let rightDeep = getDeep(root.right)if (Math.abs(leftDeep - rightDeep < 2)) {return true} else if (leftDeep > rightDeep) {// 左边深 右旋return rightRotate(root)} else {// 右边深 左旋return leftRotate(root)}
}console.log(isBalance(node2))
let newRoot = change(node2)
console.log(isBalance(newRoot))
双旋
有些情况只有一次单选是实现不了的,比如下面的情况:
变化分支(6,7)不可以是唯一的最深分支。
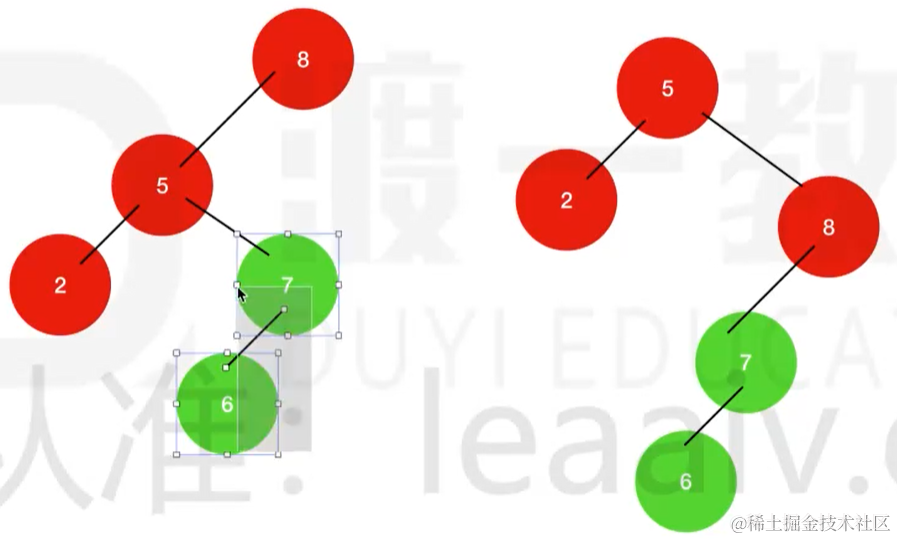
如果变化分支(6,7)是唯一的最深分支,那么需要先进行依次左旋,再进行右旋。也就是需要双旋。
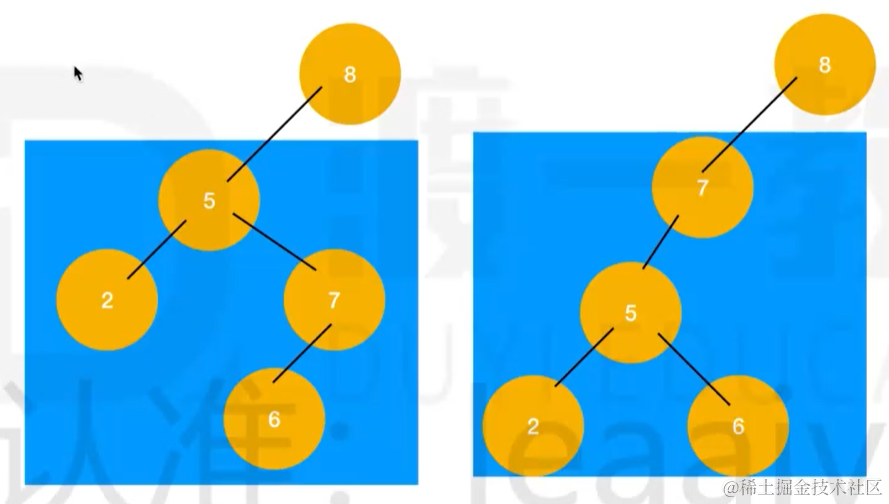
二叉树的双旋(左右双旋,右左双旋)
当要对某个节点进行左单旋时,如果变化分支是唯一的最深分支,那么我们要对新根进行右单旋,然后再进行左单旋,这样的旋转叫做右左双旋
当要对某个节点进行右单旋时,如果变化分支是惟一的最深分支,那么我们要对新根进行左单旋,然后再进行右单旋,这样的旋转叫做左右双旋