目录
形式
假设
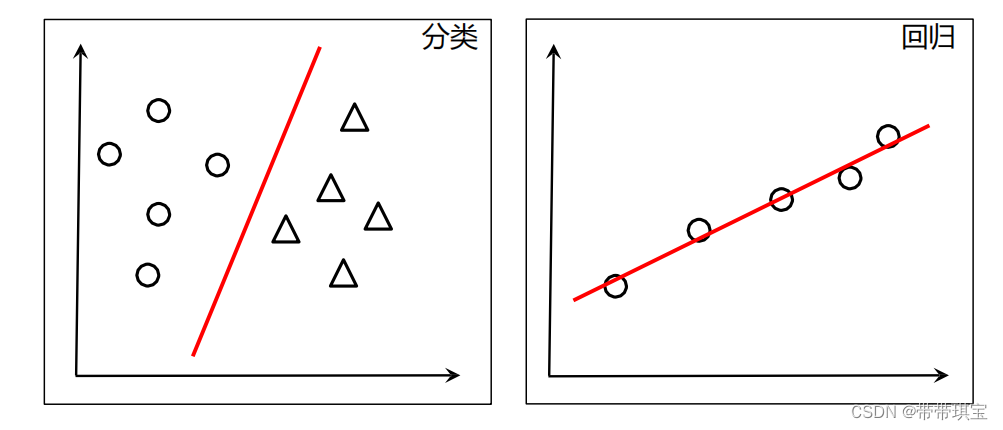
一元回归例子理解最小二乘法
多元回归
广义线性回归
对数线性回归
逻辑回归
线性判别分析
形式
线性说白了就是初中的一次函数的一种应用,根据不同的(x,y)拟合出一条直线以预测,从而解决各种分类或回归问题,假设有 n 个属性(自变量),xi 为 x 在第 i 个属性上的取值,则其形式为:
模型有系数 、
、...以及误差项
,可写为:

假设
线性回归拟合有一些重要的假设,包括:
- 因变量和自变量之间存在线性关系。
- 样本相互独立。
- 自变量之间不存在自相关。
- 误差项是独立且服从正态分布的随机变量。
- 不存在异方差现象。
一元回归例子理解最小二乘法
拿一元线性回归举例(一个自变量一个因变量):
![]()
机器学习过程中我们的目标是最小化残差平方和来估计模型系数的值,均方误差对应了常用的“欧氏距离”(Euclidean distance),目标函数如下:

(SSE就是上方的)

希望误差之和越小越好,就要对目标函数的、
求偏导使得偏导为0,该目标函数可取最值(这部分就涉及高数的内容了):
得到最优解:
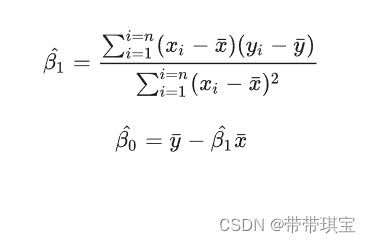
多元回归
假设有 n 个样例,m个属性,如下,每个列向量是一个属性所有样本的取值

注意,这里矩阵X的第一列为1,即最终的常数项
此时有 ,X 为矩阵,y 与 β 为列向量(理解为矩阵也一样),做乘法
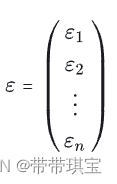
上面残差由以下公式得到
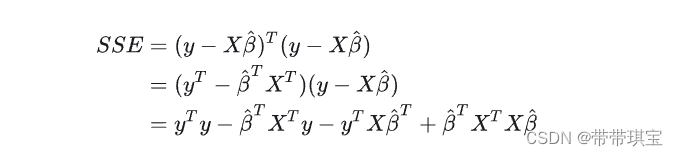
推导泛用性不大,对于过程有兴趣的可参见图片源的文章:多元线性回归(Multiple Linear Regression)详解,附python代码 - 知乎
python 中 linear_model 的 LinearRegression 可实现该方法
数据准备:
# Multiple Linear Regression# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd# Importing the dataset
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :4].values
y = dataset.iloc[:, 4].values
print(X)
print(y)# 前四列为特征
[[165349.2 136897.8 471784.1 'ShangHai'][162597.7 151377.59 443898.53 'BeiJing'][153441.51 101145.55 407934.54 'GuangZhou']
...
[0.0 135426.92 0.0 'BeiJing'][542.05 51743.15 0.0 'ShangHai'][0.0 116983.8 45173.06 'BeiJing']]# 最后一列为实际值y
[192261.83 191792.06 191050.39 182901.99 166187.94 156991.12 156122.51155752.6 152211.77 149759.96 146121.95 144259.4 141585.52 134307.35132602.65 129917.04 126992.93 125370.37 124266.9 122776.86 118474.03111313.02 110352.25 108733.99 108552.04 107404.34 105733.54 105008.31103282.38 101004.64 99937.59 97483.56 97427.84 96778.92 96712.896479.51 90708.19 89949.14 81229.06 81005.76 78239.91 77798.8371498.49 69758.98 65200.33 64926.08 49490.75 42559.73 35673.4114681.4 ]分类数据处理:
# Encoding categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
# OneHotEncoder只能处理数值型变量,对于字符型变量需要使用LabelEncoder()转化
X[:, 3] = labelencoder.fit_transform(X[:, 3]) # 用数值取代类别数据
X[:, 3]
onehotencoder=OneHotEncoder(sparse=False).fit_transform(X[:, 3].reshape(-1,1))
# ohe在对数组进行变换的时候可能需要reshape,分别代表1个样例(一行)还是1个特征(一列)
onehotencoderarray([[0., 0., 1.],[1., 0., 0.],[0., 1., 0.],...[1., 0., 0.],[0., 0., 1.],[1., 0., 0.]])线性回归对于离散值,若有序,则进行连续化,否则转化为 k 维向量
X =np.hstack((X[:,:-1],onehotencoder))
X# # Avoiding the Dummy Variable Trap 避免虚拟变量陷阱,剔除第一列变量
# X = X[:, 1:]
# 这部分待补充分割测试集训练集:
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)X_train, X_test, y_train, y_test标准化
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)
sc_y = StandardScaler()
y_train = sc_y.fit_transform(y_train.reshape(-1,1))
X_train,X_test,y_train建模
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)print(regressor.coef_) # 系数
print(regressor.intercept_) # 截距
print(regressor.score(X_train, y_train))[ 7.73467193e-01 3.28845975e-02 3.66100259e-02 8.66383692e+01-8.72645791e+02 7.86007422e+02]42467.5292485530950.9501847627493607y 的预测值:
y_pred = regressor.predict(X_test)
y_predarray([103015.20159796, 132582.27760816, 132447.73845174, 71976.09851258,178537.48221055, 116161.24230165, 67851.69209676, 98791.73374687,113969.43533012, 167921.0656955 ])广义线性回归
假设 y 与 x 不是线性关系,但 y 的变体 g(y) 与 x 是线性关系,则取反函数有:
对数线性回归
实际是广义线性回归的一个特例,简单形式为:
核心在于可以用线性关系的拟合表示出非线性的关系
逻辑回归
逻辑回归将回归应用于分类问题,对于二分类问题,有单位跃迁函数:

0与1是两个不同类别,而0.5是分界线,划分了两种不同类别,其性质不好
于是用以下 Sigmoid(逻辑函数)函数代替,可以将y的值限制在0-1之间

图像如下,函数单调可微,任意阶可导,有良好的数学性质
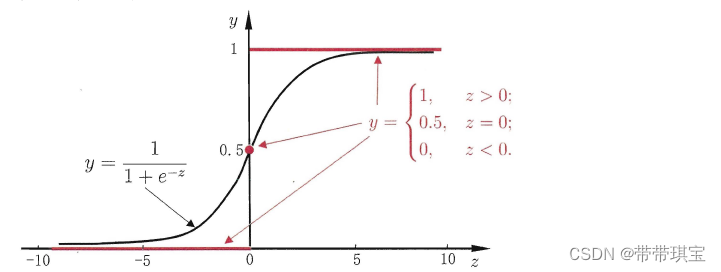
其中
则有
为什么要这样做呢?因为假设在普通的线性模型中使用 x 预测 y,是一条斜线,难以达到我们想要的(取0或1)取值。因此我们先使用 x 对 z 进行线性拟合,再使用 Sigmoid 函数将 z 的取值限制在 0-1 上
此外,由于该函数可以写为
称左边的式子其为对数几率,其中 y / (1 - y) 则为 几率(odds),表示了 x 取 1 的相对可能性。y 为样本 x 作为正例的概率,那么 1-y 则为样本 x 作为反例的概率,由此用线性模型逼近真实样本的对数几率,可在需要使用概率进行计算分析的情况提供便利,该算法优点:
- 无需事先假设数据分布
- 可得到 “类别”的近似概率预测
- 可直接应用现有数值优化算法求取最优解
线性判别分析
LDA是一种将数据降维的方法,对于这部分的数学逻辑比较复杂,暂时了解了一下原理
宗旨:找到一条线,使得所有样例的点的映射,使得同类别的点方差最小,不同类别方差最大,而衡量的标准是利用方差和协方差——不同类样例的投影点尽可能远,其矩阵协方差应该越大,而同类投影近,矩阵的方差应该越小
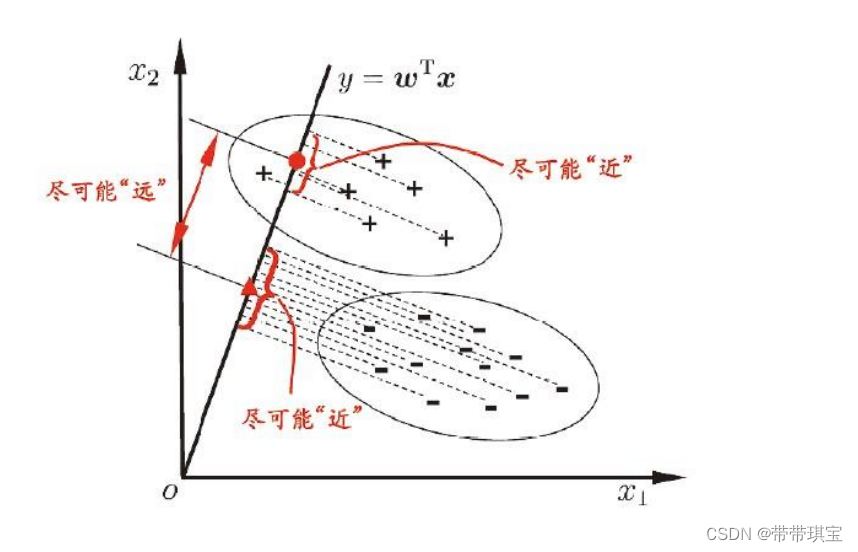
关于数学推导看得有点勉强。。有兴趣请自行搜寻