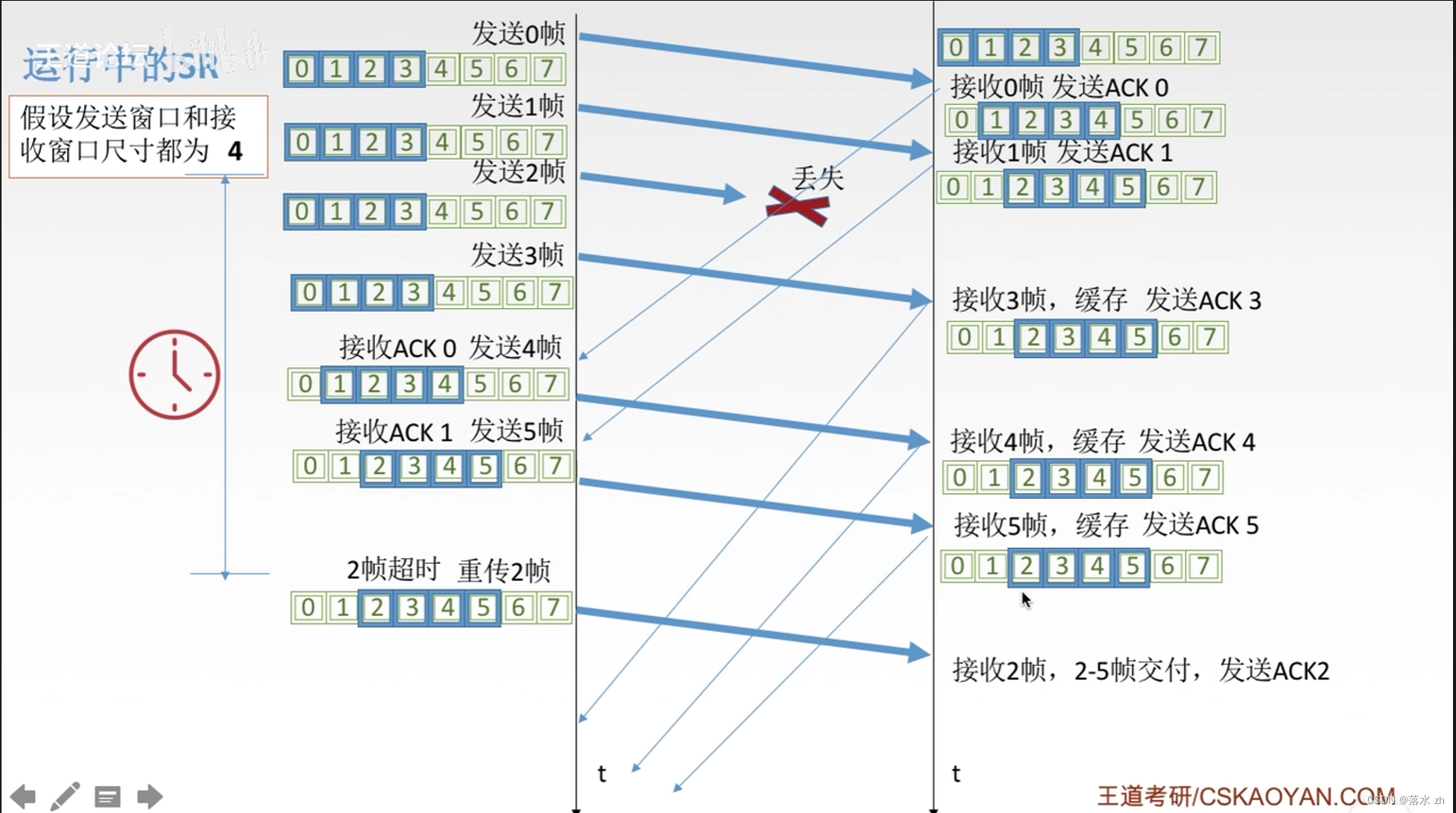
单源最短路径问题-dj

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3e5+5,M=1e6+5;
const ll INF=0x7f7f7f7f7f7f7f;//7个7f没问题,INF <= INF+x
struct edge{int to;ll w;edge(int end,ll cost){to=end;w=cost;}
};
struct node{int id;ll setdis;//id:结点;setdis:这个结点到集合内的点最短的距离node(int num,ll len){id=num;setdis=len;}bool operator <(const node& cur)const{return setdis > cur.setdis;}//小根堆按照dis的升序来排序自定义的node对象//{return cur.dis < dis;} //大根堆按照dis的降序来排序自定义的node对象//要将 < 运算符重载为适用于小根堆需要确保当 新结点cur的dis值 < 当前对象的dis值时,函数返回true。//*this(隐式参数)代表当前对象,即调用运算符重载函数的对象//将具有较小dis值的节点被放置在更接近堆顶的层次
};
vector<vector<edge>>adjtable(M);
priority_queue<node>wait;//小根堆,优先队列,存结点信息,弹出距离集合最近节点
int n,m;
ll setdis[N];//记录所有结点到集合的最近距离
bool hasmin[M];//hasmin[i]=true表示到结点i的最短路径已经找到
bool haspath[N];//如果不想用INF判定,则开个数组表示是否有通路
int pre[N];//记录前驱结点,用于生成路径
void print_path(int start,int end){ //打印从s到t的最短路if(start==end){cout<<start;return;} //打印起点print_path(start,pre[end]); //先打印前一个点cout<<end; //后打印当前点。最后打印的是终点t
}
void dj(){while(!wait.empty()){node cur = wait.top();wait.pop();//小根堆,弹出距起点start距离最小的结点minnodeif(hasmin[cur.id])continue;//丢弃已经找到最短路径的结点hasmin[cur.id]=true;haspath[cur.id]=true;//标记已访问 和有最短路径 for(edge adj:adjtable[cur.id]){//检查当前点的所有邻边if(hasmin[adj.to])continue;//丢弃已经找到最短路径的邻居结点 if(setdis[adj.to] > adj.w + cur.setdis){//如果邻点到起点的距离 大于 若当前点到起点的距离 + 邻点到当前点的边权 ,则更新邻点到起点的距离为中转当前点再过去的两端距离和 setdis[adj.to] = adj.w + cur.setdis;//邻点最短距离=邻边权重+最近点到起点的距离wait.push(node(adj.to,setdis[adj.to]));//扩展新的邻居,放到优先队列中//pre[adj.to]=cur.id; //如果有需要,记录路径
} } }
// print_path(s,n); //如果有需要,打印路径: 起点1,终点n
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);memset(setdis,INF,sizeof(setdis));//memset是按字节赋值,所以应当是0x7f
// for(ll x:sdis)x=0x7f7f7f7f7f7f7f; //循环应该是赋真值 memset(hasmin,false,sizeof(hasmin));cin>>n>>m;while(m--){int v1,v2;ll w;cin>>v1>>v2>>w;adjtable[v1].push_back(edge(v2,w));// adjtable[v2].push_back(edge(v1,w)); //无向图或重边}int start_id;//cin>>start_id;start_id=1;//haspath[start_id]可以不加,但是最好加上 wait.push(node(start_id,0));//起点进队列,起点到自己的距离是0setdis[start_id]=0;dj();for(int i=1;i<=n;++i){//输出到每个点的最短路径
// if(setdis[i]>=0x7f7f7f7f7f7f7f)cout<<"-1 ";if(!haspath[i])cout<<"-1 ";else cout<<setdis[i]<<" ";}return 0;
}