递归算法解读

递归（Recursion）是计算机科学中的一个重要概念，它指的是一个函数（或过程）在其定义中直接或间接地调用自身。递归函数通过把问题分解为更小的相似子问题来解决原问题，这些更小的子问题也使用相同的解决方案，但处理的数据规模更小。递归通常有两个关键部分：递归基准情形（base case）和递归步骤（recursive step）。

递归基准情形：是递归函数不再调用自身的情况，即问题规模缩小到可以直接解决的程度。这是递归终止的条件，确保递归过程不会无限进行下去。

递归步骤：是将问题分解为更小的子问题，并调用自身来解决这些子问题的步骤。递归步骤必须逐步缩小问题的规模，最终到达递归基准情形。

递归在解决许多问题时非常有用，如排序、搜索、遍历数据结构（如树和图）以及解决数学问题等。然而，递归也需要注意一些问题，如栈溢出（由于递归调用太深而耗尽系统栈空间）和效率问题（某些递归算法可能不如迭代算法高效）。
递归的两个特定

调用自身
结束条件

# 不是合法的递归
def func1(x):print(x)func1(x-1)# 不是合法的递归
def func2(x):if x>0:print(x)func2(x+1)# 是一个合法的递归
def func3():if x>0:print(x)func3(x-1)
# 4,3,2,1# 是一个合法的递归
def func4():if x>0:func4(x-1)print(x)
# 1,2,3,4

递归的示例1：汉诺塔问题

汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？
![外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传]
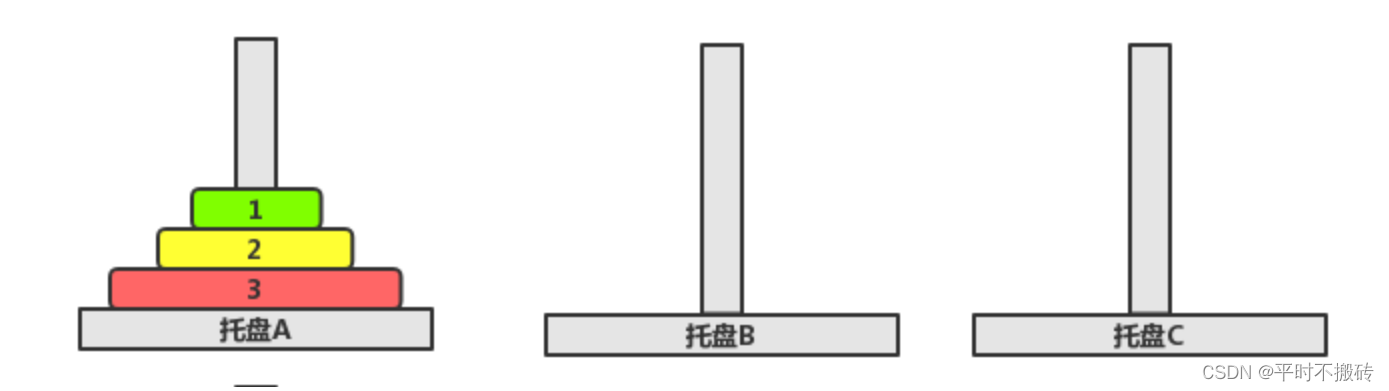
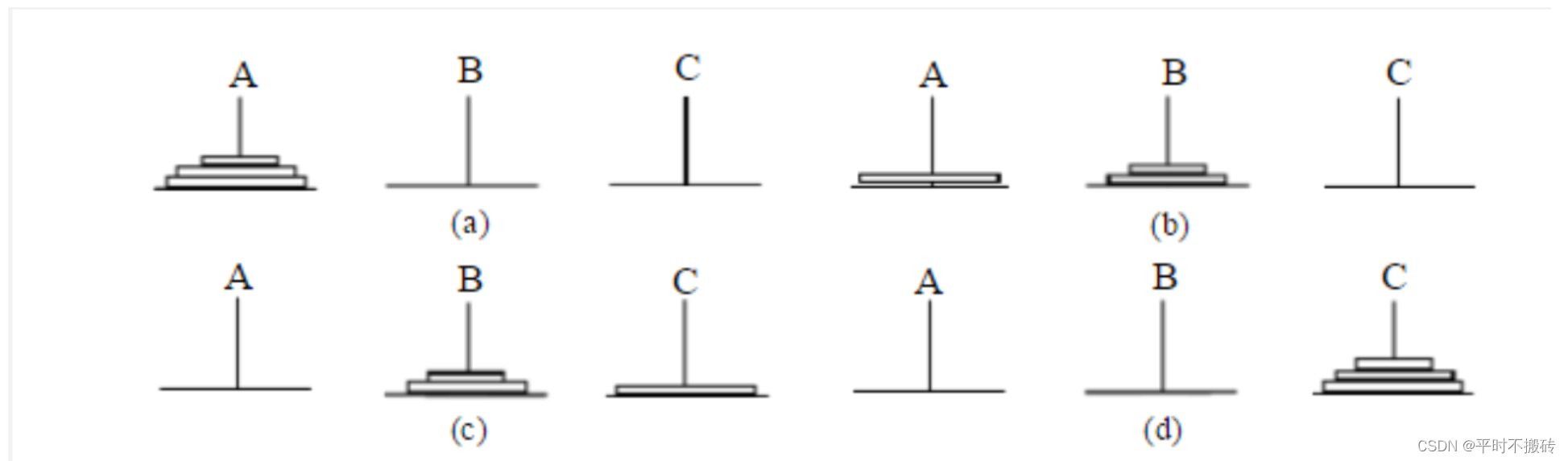
在这里插入图片描述

只有三个圆盘的时候需要这几步

将1从A移动到C，2从A移动到B，然后再1从C移动到B如图b所示
将3从A移动到C，如图c所示
将1从B移动到A，将2从B移动到C，再将1从A移动到C如图d所示。

单有n个圆盘时：

把n-1个圆盘从A经过C移动到B
把第n个圆盘从A移动到C
把n-1个圆盘从B经过A移动到C

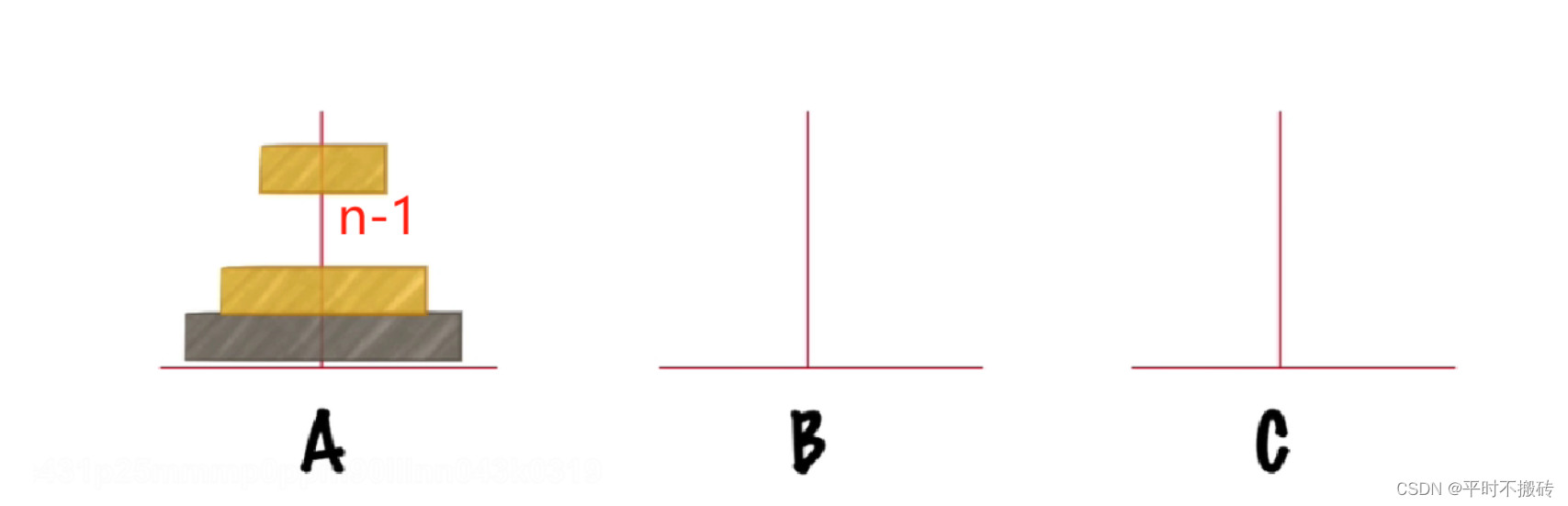
初始位置

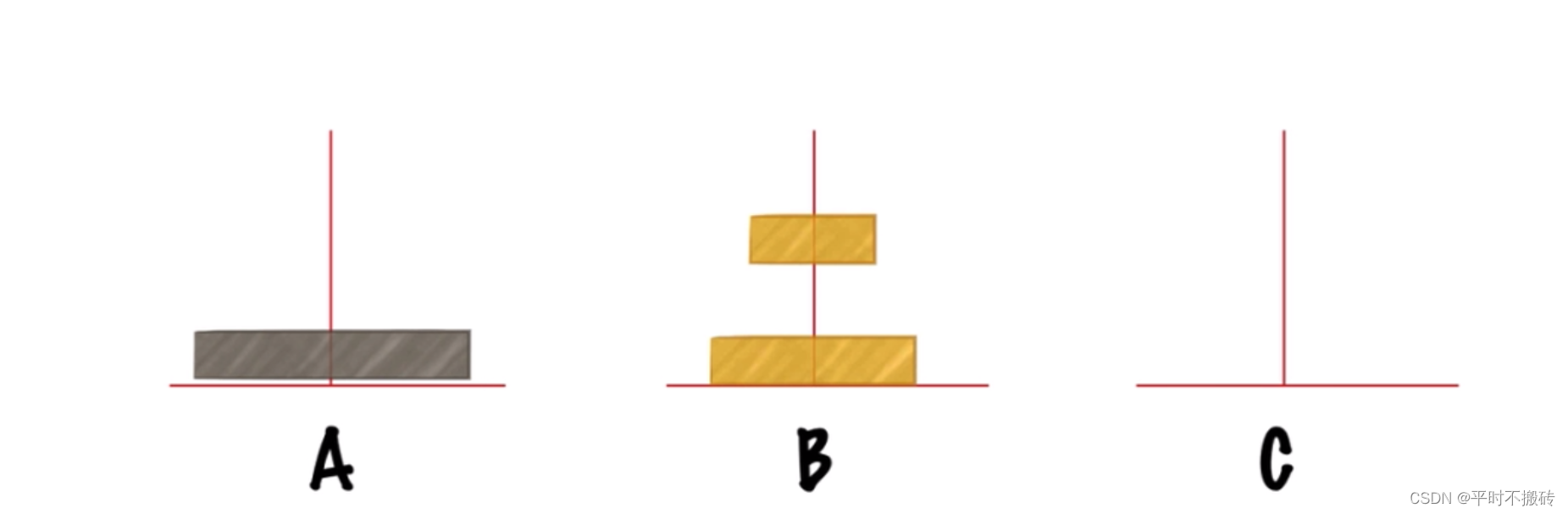
第一步把n-1个盘子从A移动到B
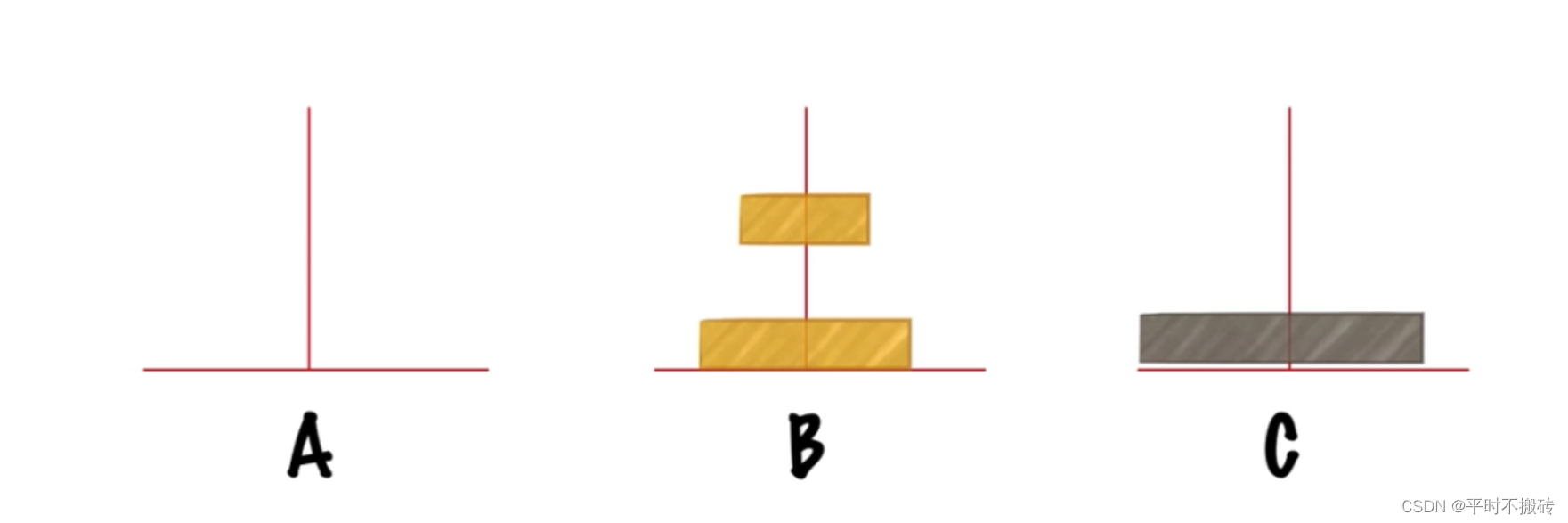
在这里插入图片描述
第二步把第n个盘中从A移动到C

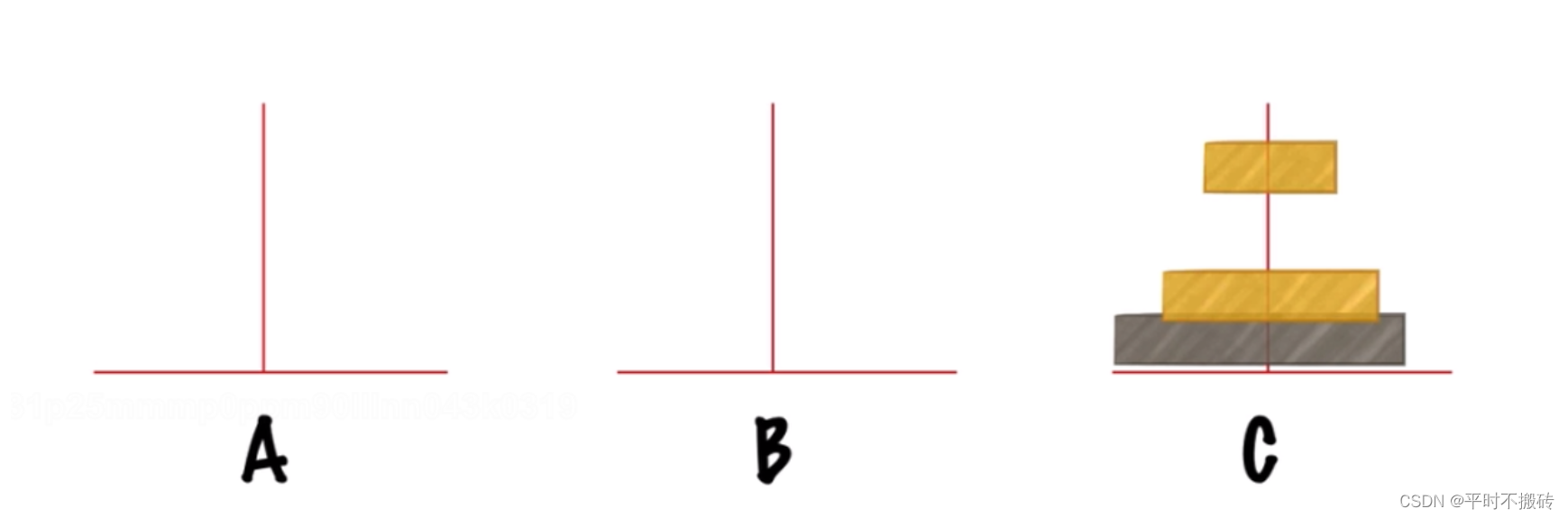
第三步把n-1个盘子从B移动到C

解题思路，把n-1个盘子当成一个整体，把问题转化为二个圆盘，移动两个圆盘无非是上面三步，将n-1个圆盘移动好了之后加上三步就是总的移动，这样就把n个圆盘的问题转化为n-1的圆盘的问题。

step = 0def hanoi(n, source, target, auxiliary):"""n：要移动的盘子数量。A：源柱子，即开始时的柱子。C：目标柱子，即要将盘子移动到的柱子。B：辅助柱子，用于在移动过程中暂存盘子。"""if n > 0:# 将n-1个盘子从源柱子移动到B柱子，目标柱子作为中转hanoi(n - 1, source, auxiliary, target)# 打印移动盘子global stepstep += 1print(f'Move disk {n} from {source} to {target}')# 将n-1个盘子从辅助柱子移动到目标柱子，源柱子作为中转hanoi(n - 1, auxiliary, target, source)# 调用函数，移动3个盘子从柱子A到柱子C，使用柱子B作为辅助
hanoi(2, 'A', 'C', 'B')
print("总的移动步数：", step)

递归的示例2：斐波那契数列

斐波那契数列就是由0和1开始，之后的斐波那契数就是由之前的两数相加而得出。比如说在斐波拉契数列当中第一个数为0，第二个数为1，因此第三个数为前面两个数之和，因此第三个数为1，同理第四个数是第二个数和第三个数之和，因此第四个数为2，下面就是斐波拉契数的变化：
$F_0 = 0\\ F_1 = 1\\ F_3 = F_0 + F_1\\ F_n = F_n-_2 + F_n-_1$
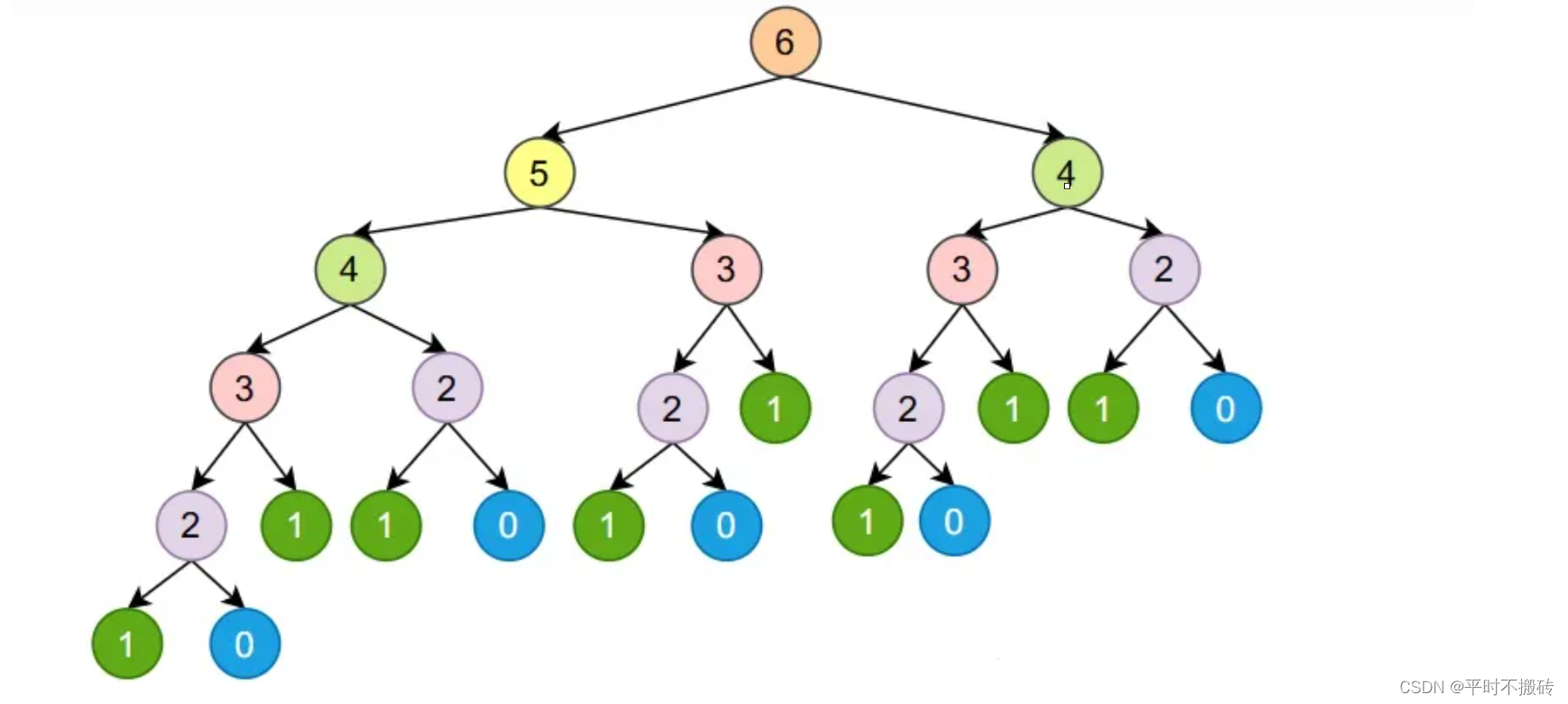
在这里插入图片描述

def fibonacci_recursive(n):if n <= 0:return "输入错误，请输入一个正整数"elif n == 1:return 0elif n == 2:return 1else:return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)# 测试函数print(fibonacci_recursive(10))  # 输出：55