2024年春季思维100活动第一阶段线上比赛（4月20日，星期六，上午）的报名正在进行中，更多安排和需要提前了解的关键点可以见我前面写的文章，或者直接联系我获取相关资料。

【提醒】2024年春季的思维100在线比赛的报名时间截止为4月6日（本周六，明天），请设置好闹钟提醒以免错过，最好今天就报名。

官方发布的2024年春季思维100活动三四五六4个年级的82道样题我已经全部做成了在线版本，可以反复刷题，吃透了这些样题，参加比赛更有胜算。

下面截图来自我制作的在线版本，答案来自官方提供，统一见文末。

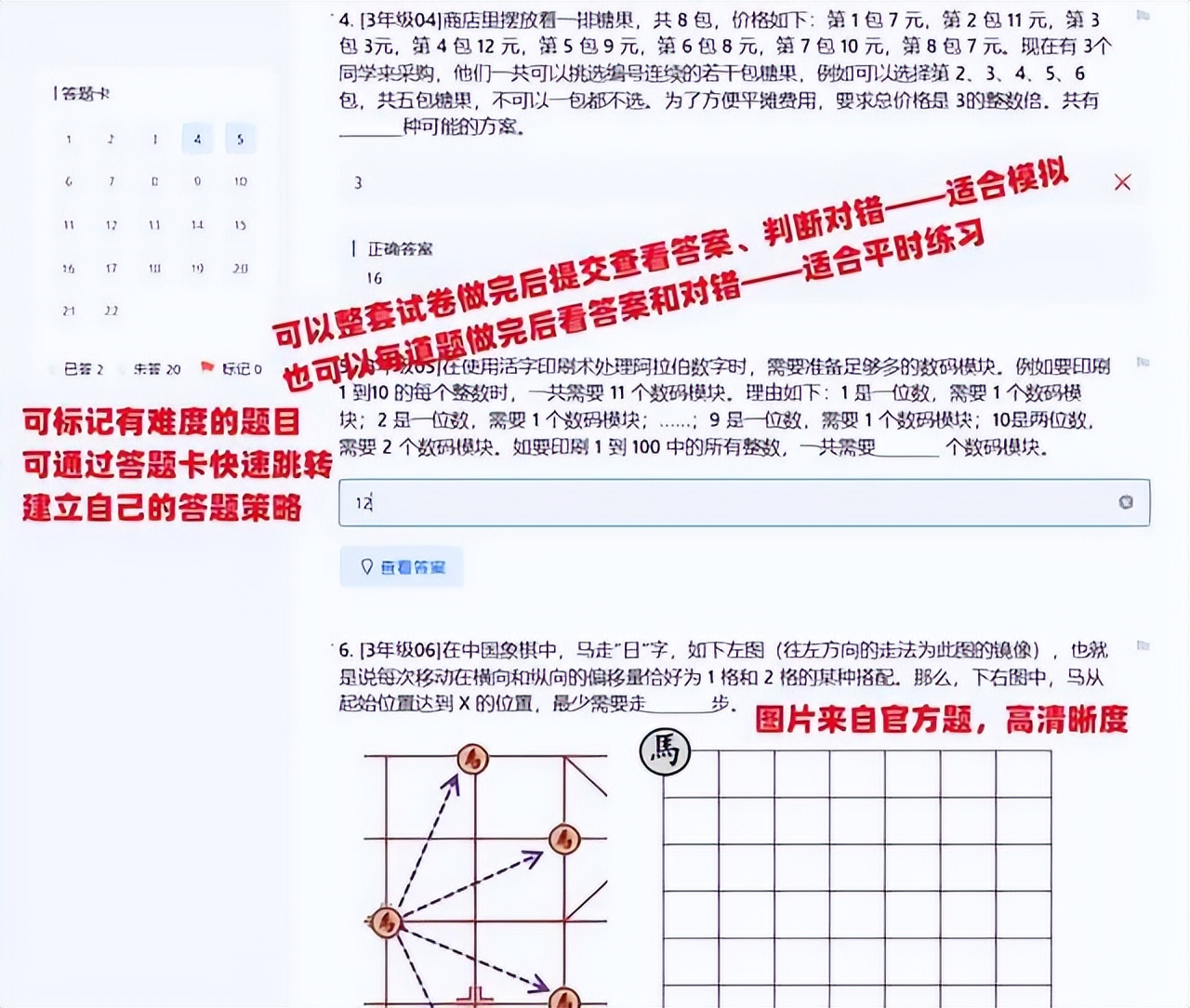
1、2024年思维100春季比赛样题-3年级第5题：

在使用活字印刷术处理阿拉伯数字时，需要准备足够多的数码模块。例如要印刷 1 到10 的每个整数时，一共需要 11 个数码模块。理由如下：1 是一位数，需要 1 个数码模块；2 是一位数，需要 1 个数码模块；……；9 是一位数，需要 1 个数码模块；10是两位数，需要 2 个数码模块。如要印刷 1 到 100 中的所有整数，一共需要________ 个数码模块。

2、2024年思维100春季比赛样题-4年级第8题：

滴水湖是位于临港的一个环形湖泊。现在要设计湖周边的景观灯光。已知在湖边均匀分布 n 盏灯，编号 1～n，每盏灯可以采用 3 种不同样式之一的灯。要求相邻的两盏灯的样式不能相同。如果 n=2，一共有 6 种不同的方案。如果 n=3，也有 6 种不同的方案。如果 n=4，一共有________种不同的方案。

3、2024年思维100春季比赛样题-5年级第4题：

在经典的“汉诺塔”游戏里，有三根杆子 A、B、C。有 4 个穿孔圆盘，盘的尺寸各不相同，目前所处位置如图，最小的圆盘在 A 处顶部，第二小的圆盘在 C 处，第三小的圆盘在 B 处，最大的圆盘在 A 处底部。要求将所有圆盘移至 C 杆，规则如下：（1）每次只能移动一个圆盘；（2）大盘不能叠在小盘上面。最少要移动________ 次，才能将所有圆盘移至 C 杆。

4、2024年思维100春季比赛样题-6年级第6题：

众所周知，在人类还没有发明计算机之前就已经有了算法的研究。欧几里得算法就是很古老的一种算法，也叫辗转相除法，用于解决最大公约数问题。

对于两个正整数 a和 b，需要求解 a 和 b 的最大公约数时，可以转换为求解 b 和(a 除以 b 的余数)的最大公约数，随着数值变小，答案就呼之欲出了。

例如：求解 49 和 35 的最大公约数，可转换为求解 35 和 14（49 除以 35 的余数为 14）的最大公约数，再转换为求解 14 和 7的最大公约数，答案显然是 7。

那么，21777 和 1309 的最大公约数是________。

---

参考答案：见本文第一条回复。下面是一些复习备考资料，欢迎了解

---

本文题目答案：

1、192；2、18；3、10；4、119。