这个是我之前就说过的要写的一篇文章，因为一直有事和别的更想写的文章就被耽误了。其实从我主观上讲我也不太愿意写这个，因为一些现实的因素，谈这个总被人曲解，所以先提早声明，我写这纯和技术有关，不针对任何公司，我不挡人财路。

      先看一个大家都听过一个道理，所谓的Transformer算力O(n)^2的关系的，这个是咋推出来的，估计大部分人不一定理解，我们现在推一下。

      Transformer 算力复杂度和n平方的关系，不是指所有，因为它包含了attention和MLP层，说这个事说的也是attention层的问题，关于Transformer网络架构的文章推荐看我的这个系列：

小周带你读论文-2之"草履虫都能看懂的Transformer老活儿新整"Attention is all you need(1) (qq.com)

      这一层为啥是O(n)^2呢，先说n是啥，n就是序列长度(我其实不愿意用n，但是大家都用n，我怕别人看不懂，我也就用n了)

      首先这一层的公式就是Q*K的转置*V，这三个东西其实维度都一样，self-attention SA的公式如下（没写多头）

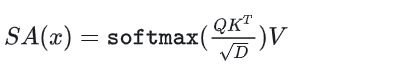
      因为本来就self-attention出来的，而且一般都等于模型的hidden_size，我们就算D吧，所以QKV都是的其中一个维度就是D，一般情况下D=hide_size h。

       QKV是怎么生成的呢？这就要先考虑问题，你喂给模型的数据x是啥样的呢？

    [B,S,H]  [batch_size,sequence_length,Dimension_size], 其中S=n，H=D, 就写成 [B,n,D]吧。

       上面的部分看不懂，强烈建议看这个系列，因为是模型训练的基础理论必备：

      LLM 参数，显存，Tflops? 训练篇(1) (qq.com)

      

      QKV都是由self-attention，也就是由输入数据self出来的，输入的数据[B,n,D]的最后一维和Wq,Wk,Wv三个矩阵是相等的。

     Wq矩阵=[D,D]，Wk和Wv也都一样, 然后输入数据分别和Wq,Wk,Wv点