算法-数论

1、最大公约数

def gcd(a,b):if b == 0:return areturn gcd(b, a%b) # a和b的最大公约数等于b与a mod b 的最大公约数def gcd(a,b):while b != 0:cur = aa = bb = cur%bpassreturn a

欧几里得算法

a可以表示成a = kb + r（a，b，k，r皆为正整数，且r不为0）

假设d是a,b的一个公约数，记作d|a,d|b，即a和b都可以被d整除。

而r = a - kb，两边同时除以d，r/d=a/d-kb/d，由等式右边可知m=r/d为整数，因此d|r

因此d也是b,a mod b的公约数。

因(a,b)和(b,a mod b)的公约数相等，则其最大公约数也相等，得证。

例题：

1、蓝桥杯2019年第十届省赛真题-等差数列 - C语言网 (dotcpp.com)

import math
n=int(input())
arr=list(map(int,input().split()))if arr[0] > arr[1]:max_ = arr[0]min_ = arr[1]
else:max_ = arr[1]min_ = arr[0]
sub = max_ -min_
for i in range(2, n):sub = math.gcd(sub, abs(arr[i]-arr[i-1]))min_ = min(min_, arr[i])max_ = max(max_, arr[i])
if max_ == min_ : print(n)
else:print((max_ - min_) // sub + 1)

2、1223. 最大比例 - AcWing题库

辗转相减法

n = int(input())
arr = list(map(int, input().split()))
arr.sort()def gcd(a,b):if b == 0:return areturn gcd(b, a%b)
top, bot = 0,0
def gcd_sub(a, b):if a < b:a,b = b,aif b==1:return areturn gcd_sub(b, a//b)
i = 1
while i < n:if arr[i] != arr[0]:gcd_ = gcd(arr[i], arr[0])top = arr[i]//gcd_bot = arr[0]//gcd_breaki += 1
if i == n:print(1)
else:for i in range(i, n):gcd_ = gcd(arr[i], arr[0])a = arr[i]//gcd_b = arr[0]//gcd_top = gcd_sub(a, top)bot = gcd_sub(b, bot)print(f'{top}/{bot}')

1.1 扩展欧几里得定律

def ext_euclid(a, b):     if b == 0:         return 1, 0, a     else:         x, y, q = ext_euclid(b, a % b) # q = gcd(a, b) = gcd(b, a%b)         x, y = y, (x - (a // b) * y)         return x, y, q

扩展欧几里得算法求系数x，y_哔哩哔哩_bilibili

例题：1299. 五指山 - AcWing题库

def olai(a, b):if b == 0:return 1,0,ax, y, gcd = olai(b, a%b)x, y = y, x-(a//b)*yreturn x, y, gcddef funt(n, d, x, y):x1, y1, gcd = olai(n, d)if (y-x)%gcd != 0:print('Impossible')else:d = y1*(y-x)//gcdn //= gcd # ax+by = n;   x = x+k*(b/gcd(a,b)); y = y+k*(a/gcd(a,b))print((d%n+n)%n)for _ in range(int(input())):n, d, x, y = map(int, input().split())funt(n, d, x, y)

2、最小公倍数

def funt(a,b):return a*b//gcd(a,b)

最小公倍数 * 最大公约数 == a*b

3、质数筛

def getPrimes(n):is_primes = [True]*(n+1)  # 初始化一个布尔数组，表示从2到n的所有数都是质数primes = [] # 存储质数for i in range(2, int(n**(1/2))+1):if is_primes[i]:primes.append(i)# 将当前质数的所有倍数标记为非质数for j in range(i*i, n+1, i): is_primes[j] = False# 后面的质数的倍数一定会超for i in range(int(n**(1/2))+1, n+1):if is_primes[i]:primes.append(i)return primes

4、区间质数筛

import mathdef simple_sieve(limit):primes = []sieve = [True] * (limit + 1)# 0和1不是质数，所以标记为Falsesieve[0] = sieve[1] = False# 从2到根号limit遍历数字for num in range(2, int(math.sqrt(limit)) + 1):if sieve[num]:primes.append(num)for multiple in range(num * num, limit + 1, num):sieve[multiple] = Falsefor num in range(int(math.sqrt(limit)) + 1, limit + 1):if sieve[num]:primes.append(num)return primesdef segmented_sieve(start, end):# 计算质数的上限limit = int(math.sqrt(end)) + 1primes = simple_sieve(limit)primes_count = len(primes)# 创建一个布尔数组，用于标记区间内的数字是否为质数，初始化为Truesieve = [True] * (end - start + 1)# 对于每一个小于等于根号end的质数for i in range(primes_count):# 计算刚好大于等于start的primes[i]的数base = max(primes[i]*primes[i], ((start + primes[i] - 1) // primes[i]) * primes[i])# 将当前质数的倍数标记为非质数for j in range(base, end + 1, primes[i]):sieve[j - start] = False# 生成区间内的质数列表segmented_primes = [start + i for i in range(end - start + 1) if sieve[i]]return segmented_primesstart = 10
end = 50
segmented_sieve(start, end)

5、欧拉函数

def funt(n):count = np = 2while p*p <= n:# 找到质因子if n % p == 0:while n % p == 0:n //= pcount -= count//p  # n*(1-p)p += 1if n > 1:count -= count//nreturn count
funt(20)

欧拉函数公式证明_哔哩哔哩_bilibili

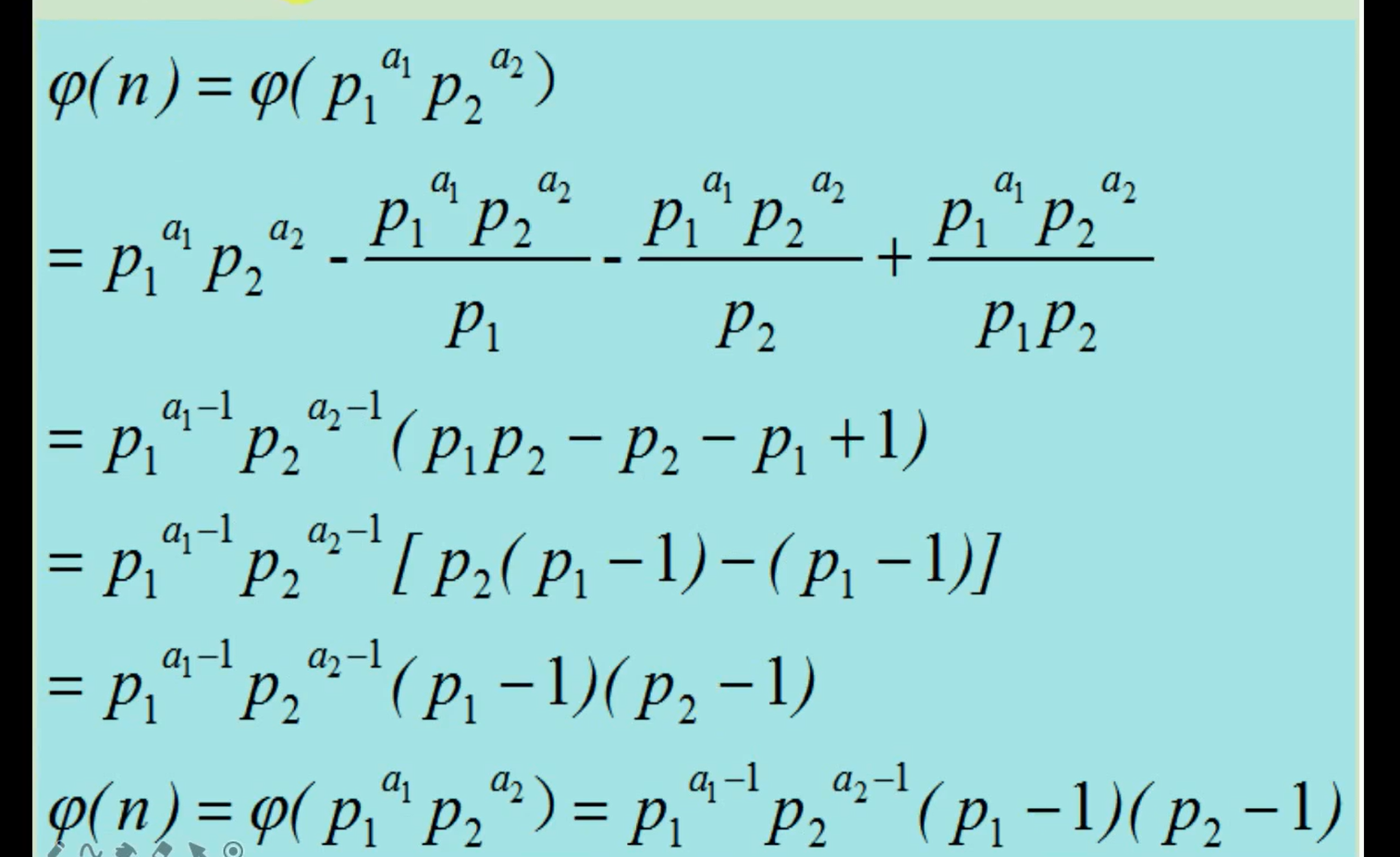
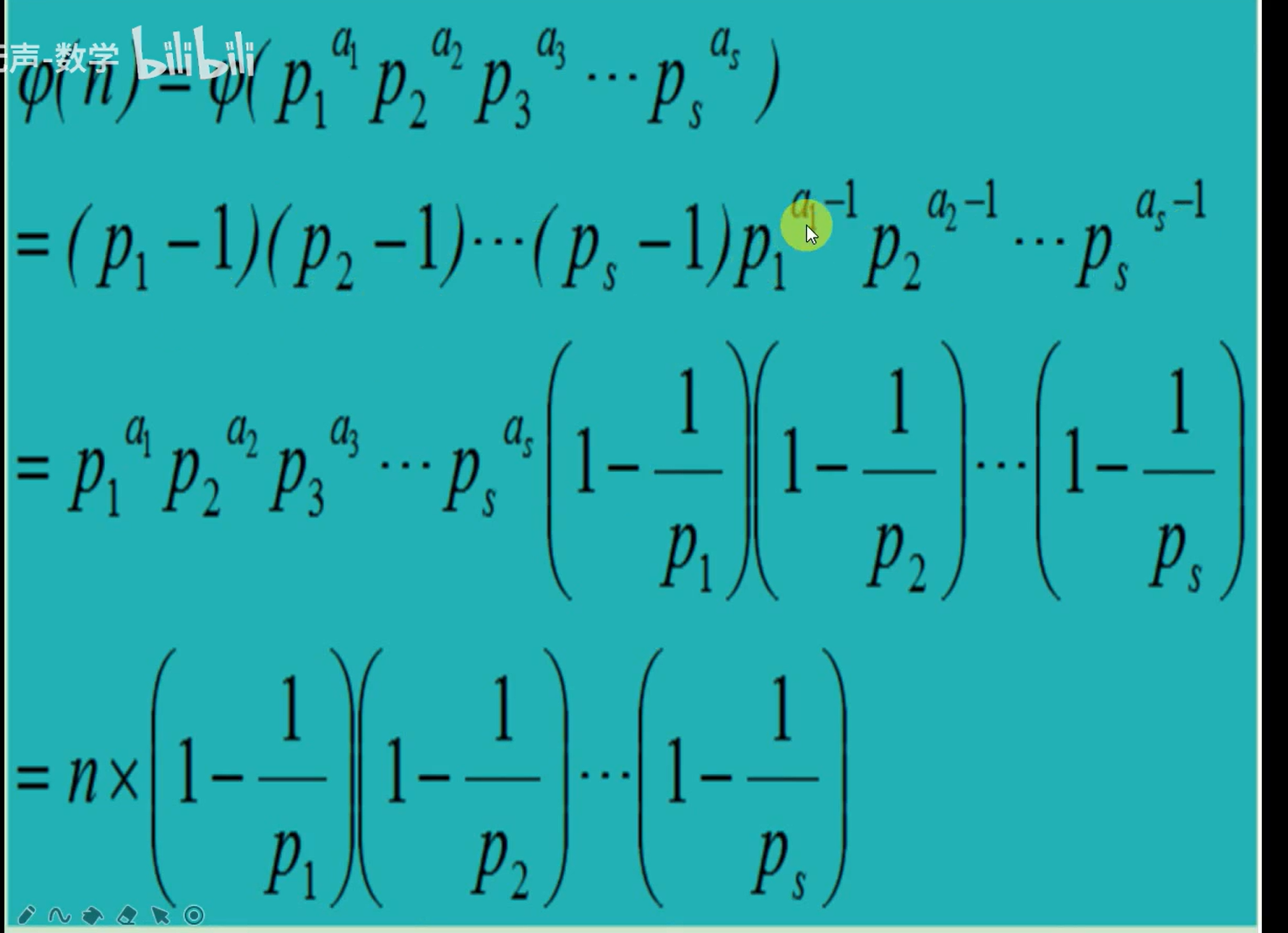
6、计算质因子个数

def funt(n):count = 0p = 2while p * p <= n:if n % p == 0:count += 1while n % p == 0:n //= pp += 1if n > 1:count += 1return count
funt(12) 

7、计算所有约数个数

约数，又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数，就说a能被b整除，或b能整除a。a称为b的倍数，b称为a的约数。

def funt(n):count = 1p = 2while p*p <= n:cnt = 0while n%p == 0:cnt += 1n //= pcount *= (cnt+1)if n>1:count *= 2return count
funt(12)

如12：12可以写成2 ** 2 *3，所以 对于2的选择有3种，幂为0、1、2；3的选择有两种，幂为0、1.

相乘即为约数和

8、计算所有约数和

def funt(n):cnt = 0p = 1while p*p <= n:# 一次算两个约数if n%p == 0:cnt += p# 平方就只用算一次if p*p != n:cnt += n//pp += 1return cnt
funt(12)

例题

1295. X的因子链 - AcWing题库

# 方法一 动规  
def funt(n):primes = [n]p = 2while p*p <= n:if n%p == 0:primes.append(p)if p*p != n:primes.append(n//p)p += 1if n>1 and n != primes[0]:primes.append(n)primes.sort()dp = [[1]*len(primes) for _ in range(2)]for i in range(1, len(primes)):max_ = cnt = 0for j in range(i):if primes[i] % primes[j] == 0:if dp[0][j] > max_:cnt = dp[1][j]max_ = dp[0][j]elif dp[0][j] == max_:cnt += dp[1][j]dp[0][i],dp[1][i] = max_+1, cnt if cnt else 1print(dp[0][-1], dp[1][-1])
while True:try:n = int(input())funt(n)except EOFError:break# 数学！！！ https://www.acwing.com/solution/content/97535/ 具体请看题解，我实在不知道怎么表达o(´^｀)o
def A(a, b):cnt = 1while b > 0:cnt *= aa -= 1b -= 1return cntdef funt(n):cnt = []p = 2while p*p <= n:if n%p == 0:cnt_ = 0while n%p == 0:cnt_ += 1n //= pcnt.append(cnt_)p += 1if n>1:cnt.append(1)sum_ = sum(cnt)a = 1for i in cnt:if i > 1:a *= A(i,i)times = A(sum_, sum_)//aprint(sum_, times)
while True:try:n = int(input())funt(n)except EOFError:break

9、快速幂

# n为负数则最终结果返回 1/pow(x,-n)
def pow(x, n):if n < 2:return x**nret = pow(x, n//2)if n%2:return ret*ret*xreturn ret*ret
pow(2, 10)

1:
a *= A(i,i)
times = A(sum_, sum_)//a
print(sum_, times)
while True:
try:
n = int(input())
funt(n)
except EOFError:
break

## 9、快速幂```Python
# n为负数则最终结果返回 1/pow(x,-n)
def pow(x, n):if n < 2:return x**nret = pow(x, n//2)if n%2:return ret*ret*xreturn ret*ret
pow(2, 10)