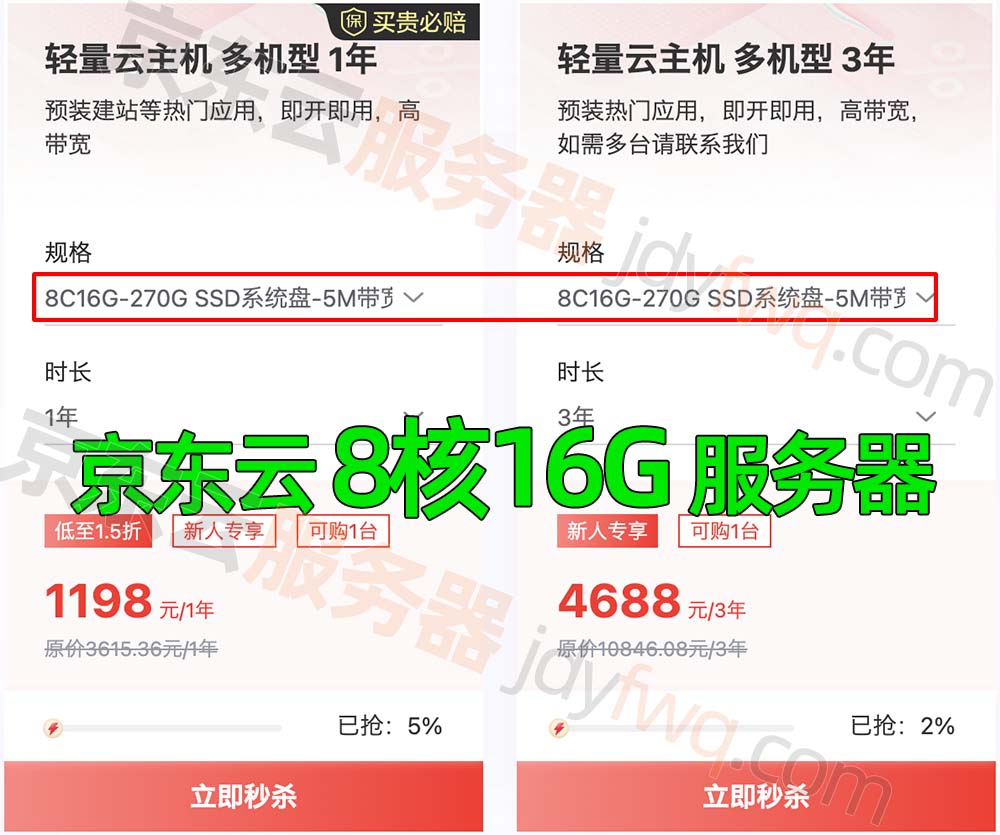
图片来源：@_snowstorm_

路线问题的状态表示一般都可以用点的坐标来表示

状态表示数组维数的确定原则：在可以用该维数表示出答案的基础上维数尽可能最小

数字三角形

acwing 898

#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;const int N = 510;int f[N][N]; //f[i][j]:从底向上走到(i,j)所有点的集合
int n;int main(){cin >> n;for(int i = 1;i <= n;i ++ ){for(int j = 1;j <= i;j ++ ){cin >> f[i][j];}}for(int i = n - 1;i;i -- ){for(int j = 1;j <= i;j ++ ){f[i][j] += max(f[i + 1][j],f[i + 1][j + 1]);}}cout << f[1][1] << endl;return 0;
}

最长严格上升子序列 (时间复杂度O(n ^ 2))

acwing 895

#include<iostream>
#include<algorithm>
#include<climits>using namespace std;const int N = 1010;int n;
int a[N],f[N]; //f[i]表示所有以第i个数结尾的上升子序列的最大值int main(){cin >> n;for(int i = 1;i <= n;i ++ ){cin >> a[i];}for(int i = 1;i <= n;i ++ ){f[i] = 1;for(int j = 1;j < i;j ++ ){if(a[j] < a[i]) f[i] = max(f[j] + 1,f[i]);}}int res = INT_MIN;for(int i = 1;i <= n;i ++ ){res = max(res,f[i]);}cout << res << endl;return 0;
}

最长严格上升子序列（二分优化）(时间复杂度O(nlogn))

二分优化后像贪心的思想

acwing896

#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n;
int a[N];
int q[N];int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);int len = 0;q[0] = -2e9;for(int i = 0; i < n; i ++ ){int l = 0, r = len + 1;while(l < r){int mid = l + r >> 1;if(q[mid] >= a[i]) r = mid;else l = mid + 1;}len = max(len, l);q[l] = a[i];}cout << len << endl;return 0;
}

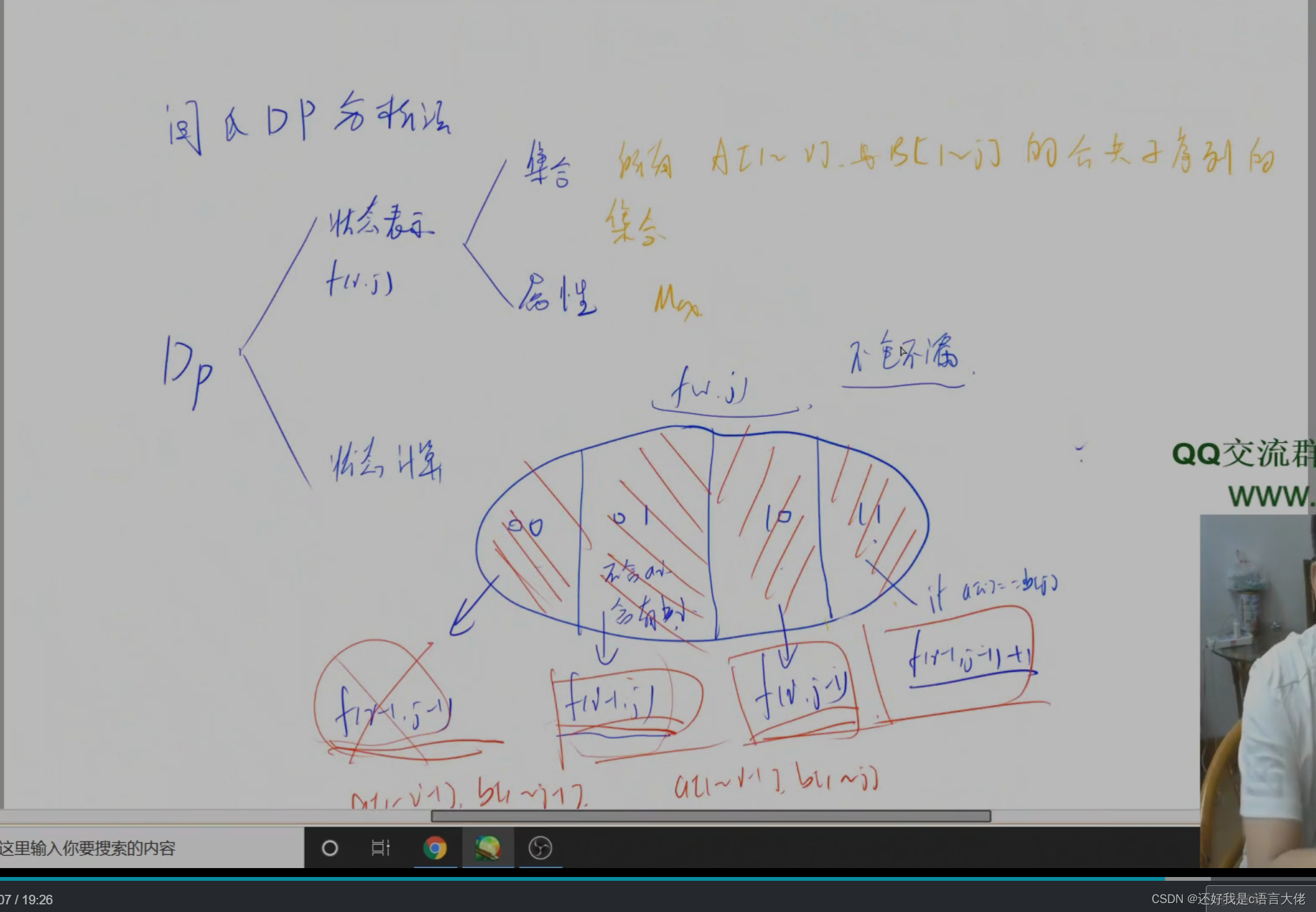
最长公共子序列 

acwing 897

#include<cstring>
#include<iostream>using namespace std;const int N = 1010;int n, m;
string a, b;
int f[N][N];int main()
{cin >> n >> m;cin >> a >> b;for(int i = 1; i <= n; i ++ )for(int j = 1; j <= m; j ++ ){f[i][j] = max(f[i][j - 1], f[i - 1][j]);if(a[i - 1] == b[j - 1]) f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);}cout << f[n][m] << endl;return 0;
}