目录
1、毕业旅行问题(今日头条2019笔试题)
2、蒙德里安的梦想(算法竞赛进阶指南)
3、最短Hamilton路径(《算法竞赛进阶指南》&模板)
4、国际象棋(第十二届蓝桥杯省赛第二场C++ A组/B组)
5、小国王(《信息学奥赛一本通》 SGU223)
1、毕业旅行问题(今日头条2019笔试题)
小明目前在做一份毕业旅行的规划。
打算从北京出发,分别去若干个城市,然后再回到北京,每个城市之间均乘坐高铁,且每个城市只去一次。
由于经费有限,小明希望能够通过合理的路线安排尽可能的省些路上的花销。
给定一组城市和每对城市之间的火车票的价钱,找到每个城市只访问一次并返回起点的最小车费花销。
注意:北京为 1 号城市。
输入格式
第一行包含一个正整数 n,表示城市个数。
接下来输入一个 n 行 n 列的矩阵,表示城市间的车票价钱。
输出格式
输出一个整数,表示最小车费花销。
数据范围
1<n≤20,包括北京
车票价格均不超过 1000 元。
输入样例:
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
输出样例:
13
说明
共 4 个城市,城市 1 和城市 1 的车费为0,城市 1 和城市 2 之间的车费为 2,城市 1 和城市 3 之间的车费为 6,城市 1 和城市 4 之间的车费为 5,以此类推。
假设任意两个城市之间均有单程票可买,且价格均在 1000 元以内,无需考虑极端情况。
思路:
经典的状态压缩求最短路问题,每个城市只有两个状态:去过或者没去过,去过则为1,没去过则为0

代码:
#include<bits/stdc++.h>using namespace std;int n; const int N=20,M=1<<20;int w[N][N];int f[M][N];//M表示状态的压缩,N代表最后到哪一个城市了 int main()
{cin>>n;memset(f,0x3f,sizeof f);//每个状态为正无穷,表示还没取min for(int i=0;i<n;i++){for(int j=0;j<n;j++){scanf("%d",&w[i][j]);}}f[1][0]=0;//初始的状态(需要费用为0) //从1开始表示北京已经去过了 (二进制表示为000.....1) for(int i=1;i<1<<n;i++)//(1<<n)-1就是111....1//例如n==5的时候,1<<5就是100000,减去1就是11111 {for(int j=0;j<n;j++)//北京开始 {//这个状态下(终点为j,状态为i) if(i>>j&1)//(i>>j表示要到第j个城市,这个状态的j位就要是1(否则到不了)) {for(int k=0;k<n;k++)//从第k个城市转移过来{if((i-(1<<j))>>k&1)//i中减去第j个城市后还包含k//说明这个状态到过k,可以从k转移过来f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]); } }}}int res=1<<31-1;for(int i=1;i<n;i++){res=min(res,f[(1<<n)-1][i]+w[i][0]);}cout<<res;return 0;
} 2、蒙德里安的梦想(算法竞赛进阶指南)
求把 N×M 的棋盘分割成若干个 1×2 的长方形,有多少种方案。
例如当 N=2,M=4 时,共有 5 种方案。当 N=2,M=3,时,共有 3 种方案。
如下图所示:
![]()
输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 N 和 M。
当输入用例 N=0,M=0 时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
1≤N,M≤11
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例:
1
0
1
2
3
5
144
51205
思路:
先放置完横着放的,之后竖着放的方法就是固定的
一个重要的任务就是判断放置的方法是否合法
基本框架:

预处理:
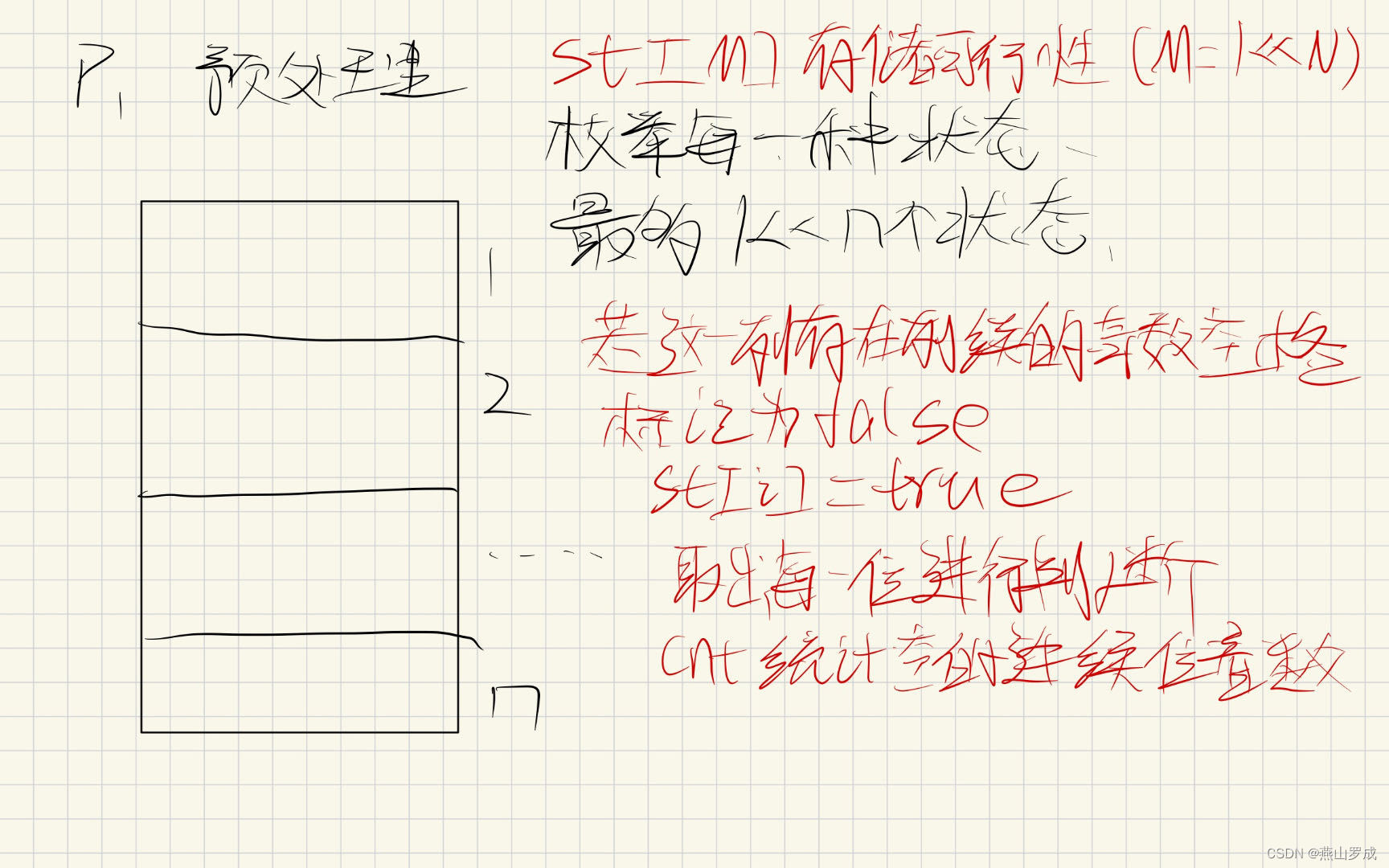
dp:

代码:
#include<bits/stdc++.h>using namespace std;const int N=12;
const int M=1<<11;int n,m;long long f[N][M];//第i列的状态为M ,j表示出头的方格数量 bool st[M];//用来表示某一种状态是否合法 int main()
{while(cin>>n>>m,n || m){memset(f,0,sizeof f);//开始预处理for(int i=0;i<1<<n;i++)//枚举每一种状态 {int cnt=0;//记录连续的空格数量 st[i]=true; for(int j=0;j<n;j++){if(i>>j&1)//这个位置不是空格 {if(cnt&1)st[i]=false;//这个位置之前的连续空格数量是奇数,不合法 cnt=0;}else cnt++;}if(cnt&1)st[i]=false; }f[0][0]=1;//第0列没有上一列,所以没有戳出来的//小方块里什么都没有放,只有这一种状态 for(int i=1;i<=m;i++)//枚举列 {for(int j=0;j<1<<n;j++)//枚举这一列的状态 {for(int k=0;k<1<<n;k++)//枚举上一列的状态 {if(((j&k)==0) && st[j|k])//(k列加上j列向后伸的格子后要合法){f[i][j]+=f[i-1][k];}}}} cout<<f[m][0]<<endl;}return 0;
}3、最短Hamilton路径(《算法竞赛进阶指南》&模板)
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x],并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤1e7
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18思路:
状态压缩dp模板
代码:
#include<bits/stdc++.h>using namespace std;const int N=20,M=1<<20;int n;int w[N][N];int f[M][N];int main()
{int n;cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){scanf("%d",&w[i][j]);}}//状态压缩dp memset(f,0x3f,sizeof f);//初始为0f[1][0]=0;//i==1表示第一个点已经走了,j==0表示目前在第一个点 //从0000.。。1开始 for(int i=1;i<1<<n;i++){//从起点0开始 for(int j=0;j<n;j++){//只有i包含j这个点,才能从i这个状态转移到终点为j的状态 if(i>>j&1){//f[i][k]---k-jfor(int k=0;k<n;k++){if((i-(1<<j))>>k&1){//(用不包含j点的状态来转移)f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);}}}}}int res=1<<31-1;//for(int i=1;i<n;i++)//{// res=min(res,f[(1<<n)-1][i]);//}//cout<<res<<endl;//标明了终点是n-1,所以说直接选终点是n-1的情况 cout<<f[(1<<n)-1][n-1];return 0;
}4、国际象棋(第十二届蓝桥杯省赛第二场C++ A组/B组)
众所周知,“八皇后” 问题是求解在国际象棋棋盘上摆放 8 个皇后,使得两两之间互不攻击的方案数。
已经学习了很多算法的小蓝觉得 “八皇后” 问题太简单了,意犹未尽。作为一个国际象棋迷,他想研究在 N×M 的棋盘上,摆放 K 个马,使得两两之间互不攻击有多少种摆放方案。
由于方案数可能很大,只需计算答案除以 1000000007 (即 1e9+7) 的余数。
如下图所示,国际象棋中的马摆放在棋盘的方格内,走 “日” 字,位于 (x,y)格的马(可以攻击 (x+1,y+2)、(x+1,y−2)、(x−1,y+2)、(x−1,y−2)、(x+2,y+1)、(x+2,y−1)、(x−2,y+1) 和 (x−2,y−1) 共 8 个格子。
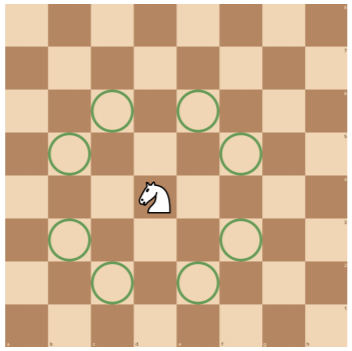
输入格式
输入一行包含三个正整数 N,M,K分别表示棋盘的行数、列数和马的个数。
输出格式
输出一个整数,表示摆放的方案数除以 1000000007(即 1e9+7) 的余数。
数据范围
对于 5%5% 的评测用例,K=1;
对于另外 10%10% 的评测用例,K=2;
对于另外 10%10% 的评测用例,N=1;
对于另外 20%20% 的评测用例,N,M≤6,K≤5;
对于另外 25%25% 的评测用例,N≤3,M≤20,K≤12;
对于所有评测用例,1≤N≤6,1≤M≤100,1≤K≤20。
输入样例1:
1 2 1
输出样例1:
2
输入样例2:
4 4 3
输出样例2:
276
输入样例3:
3 20 12
输出样例3:
914051446思路:
枚举思路:

代码:
#include<bits/stdc++.h>using namespace std;
typedef long long LL;
const int N = 110,M=6,MOD=1e9+7;
int f[N][1<<M][1<<M][21];
int n,m,k;
int get_count(int x)//返回x的二进制有多少个1
{int res=0;while(x){res++;x-=(x&-x);}return res;
}
int main()
{scanf("%d%d%d",&n,&m,&k);f[0][0][0][0]=1;//状态初始化:第0行时,状态只能是0,只能是放0个马//5层循环比较乱,把图画出来,照着图写for(int i=1;i<=m;i++){for(int c=0;c<1<<n;c++){for(int a=0;a<1<<n;a++){if((c&(a<<2))||(a&(c<<2))) continue;for(int b=0;b<1<<n;b++){if(b&(a<<2)||a&(b<<2)) continue;if(b&(c<<1)||c&(b<<1)) continue;int t=get_count(b);for(int j=t;j<=k;j++)f[i][a][b][j]=(f[i][a][b][j]+f[i-1][c][a][j-t])%MOD;//对应集合划分,枚举j,f[i-1][c][a][j-t]都能到达f[i][a][b][j]}}}}int res=0;for(int a=0;a<1<<n;a++){for(int b=0;b<1<<n;b++){res=(res+f[m][a][b][k])%MOD;//m,k固定,a,b随意}}printf("%d",res);return 0;
}
5、小国王(《信息学奥赛一本通》 SGU223)
在 n×n 的棋盘上放 k 个国王,国王可攻击相邻的 8 个格子,求使它们无法互相攻击的方案总数。
输入格式
共一行,包含两个整数 n 和 k。
输出格式
共一行,表示方案总数,若不能够放置则输出0。
数据范围
1≤n≤10,
0≤k≤n**2
输入样例:
3 2
输出样例:
16思路:

代码:
#include<bits/stdc++.h>using namespace std;typedef long long LL;const int N = 11, M = 1 << N, C = N * N;int n, m, K;
LL f[N][C][M];
int cnt[M];
vector<int> legal_state;
vector<int> state_trans[M];bool check(int state)
{return !(state & state >> 1);
}
int count(int state)
{int res=0;while(state){res++;state-=state & -state;}return res;
}
int main()
{cin >> n >> K;//预处理所有合法状态for (int st = 0; st < 1 << n; ++ st)//检查当前状态是否合法if (check(st))legal_state.push_back(st),cnt[st] = count(st);m = legal_state.size();//预处理所有合法状态的合法转移for (auto cur_st: legal_state)for (auto to_st: legal_state)if (!(cur_st & to_st) && check(cur_st | to_st))//上下不相邻且纵坐标也不相邻state_trans[cur_st].push_back(to_st);//动态规划f[0][0][0] = 1;for (int i = 1; i <= n; ++ i)for (int j = 0; j <= K; ++ j)for (auto &state: legal_state)for (auto &pre_st: state_trans[state])if (j - cnt[state] >= 0)f[i][j][state] += f[i - 1][j - cnt[state]][pre_st];//统计目标状态的所有方案数LL res = 0;for (auto state: legal_state) res += f[n][K][state];cout << res << endl;return 0;
}