01背包(二维dp数组)
背包最大重量为4。
物品为:
| 重量 | 价值 | |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
背包能背的物品最大价值是?
动规五步曲:
- dp数组的含义:dp[i][j] 表示从下标为 [0 - i] 的物品里任取,放入容量为 j 的背包,价值总和最大是多少。(如下图所示)
- 递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])。对于每个物品,都有放于不放2种选择。如果不放第 i 件物品,dp[i][j] = dp[i - 1][j]。如果放第 i 件物品,dp[i][j] = dp[i - 1][j - weight[i]] + value[i](需要确保背包容量足够,否则 j - weight[i] 为负)。
- 初始化:根据递推公式,dp[i][j] 由左上角推出,我们应该初始化第一行 dp[0][j] 和第一列 dp[i][0]。dp[0][j] 容量小于 物品0重量的时候为0,大于等于 物品0重量的时候为物品0重量。dp[i][0] 表示背包容量为 0,无法放入任何物品,因此 dp[i][0] = 0。
- 遍历顺序:先遍历物品还是先遍历背包都是可以的。
- 打印dp数组



def test_2_wei_bag_problem1():weight = [1, 3, 4] # 物品的重量列表value = [15, 20, 30] # 对应物品的价值列表bagweight = 4 # 背包的最大容量# 初始化动态规划表,行数为物品数量,列数为背包容量+1(从0到bagweight)# dp[i][j]表示在前i件物品中,对于容量为j的背包,可以获得的最大价值dp = [[0] * (bagweight + 1) for _ in range(len(weight))]# 初始化第一行,仅考虑第一件物品时的情况# 当背包容量大于等于第一件物品的重量时,可以选择放入这件物品for j in range(weight[0], bagweight + 1):dp[0][j] = value[0]# 逐个考虑剩下的物品for i in range(1, len(weight)): # 遍历物品for j in range(bagweight + 1): # 遍历背包容量# 如果当前背包容量小于物品i的重量,则物品i不能加入背包# 此时,最大价值与不考虑物品i时相同if j < weight[i]:dp[i][j] = dp[i - 1][j]# 否则,需要决定是加入物品i还是不加入# 加入物品i的情况下,最大价值为加入物品i之前的最大价值加上物品i的价值# 不加入物品i的情况下,最大价值与不考虑物品i时相同# 取两者的较大值else:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])# 输出最终结果:所有物品考虑完毕后,容量为bagweight的背包可以获得的最大价值print(dp[len(weight) - 1][bagweight])01背包(一维dp数组)
使用一维数组时,数组的每个元素
dp[j]表示对于当前考虑的物品,容量为j的背包所能装入的最大价值。关键在于更新这个数组时需要从后往前更新,这样可以保证在更新dp[j]时,dp[j-weight[i]]仍然代表没有考虑当前物品时的状态。
动规五步曲:
- dp数组的含义:dp[j] 表示容量为 j 的背包,价值总和最大是多少。
- 递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])。
- 初始化:dp[0] = 0,因为背包容量为0所背的物品的最大价值就是0。其他下标应该初始化多少呢?看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
- 遍历顺序:倒序遍历,01背包问题由于每个物品只有一个,正序遍历会导致同一个物品被多次加入背包。
- 打印dp数组
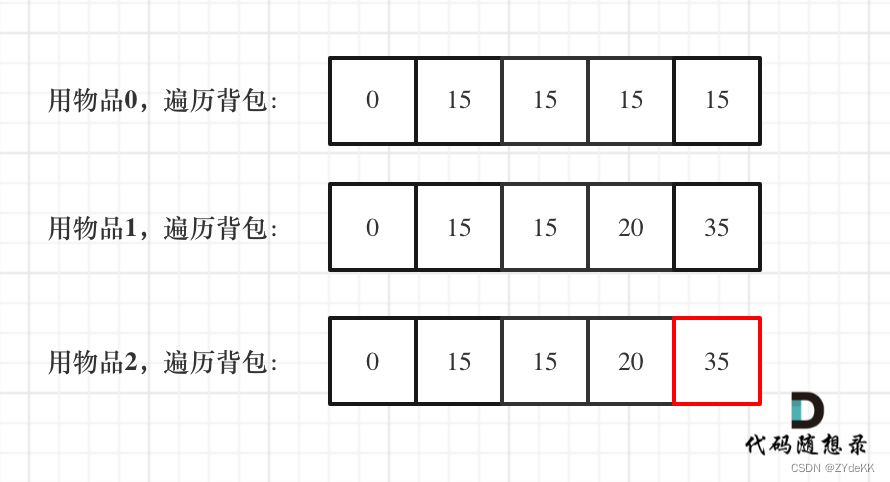
def test_2_wei_bag_problem1_optimized():weight = [1, 3, 4]value = [15, 20, 30]bagweight = 4# 初始化一维数组dp = [0] * (bagweight + 1)# 遍历物品for i in range(len(weight)):# 从后往前遍历背包容量# 注意这里的范围是 weight[i] 到 bagweight# 这是因为当背包容量小于物品重量时,该物品无法被选中for j in range(bagweight, weight[i]-1, -1):# 更新dp[j]dp[j] = max(dp[j], dp[j - weight[i]] + value[i])print(dp[bagweight])416.分割等和子集
动规五步曲:
- dp数组的含义:dp[j] 表示容量为 j 的背包,价值总和最大是多少。
- 递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]), 物品i的重量和价值都是nums[i]。
- 初始化:dp[0] = 0,从dp[j]的定义来看,首先dp[0]一定是0。如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
- 遍历顺序:倒序遍历,01背包问题由于每个物品只有一个,正序遍历会导致同一个物品被多次加入背包。
- 打印dp数组
class Solution:def canPartition(self, nums: List[int]) -> bool:# 如果数组的总和是奇数,直接返回False,因为无法分割成两个和相等的子集if sum(nums) % 2 != 0:return False# 计算目标和,即分割后每个子集应该达到的和target = sum(nums) // 2# 初始化动态规划数组,dp[j]存储的是能够通过选择数组nums中的若干个数,其总和最多能达到j的值dp = [0] * (target + 1)# 遍历每一个数字,尝试更新dp数组for num in nums:# 从后向前遍历,确保每个数字只被计算一次# 这里遍历到num是因为,当背包容量小于当前数字重量时,无法选择当前数字for j in range(target, num - 1, -1):# 更新dp[j],dp[j]是当前容量为j时能达到的最大和# 选择当前数字和不选择当前数字的最大值dp[j] = max(dp[j], dp[j - num] + num)# 如果dp数组的最后一个元素(即dp[target])等于目标和,说明可以分割成两个和相等的子集return dp[-1] == targetclass Solution:def canPartition(self, nums: List[int]) -> bool:# 回溯(超时)total_sum = sum(nums)# 如果总和是奇数,则无法分割成两个和相等的子集if total_sum % 2 != 0:return Falsetarget = total_sum // 2def dfs(index, current_sum):# 如果当前子集的总和等于目标和,则找到了一个解if current_sum == target:return True# 如果当前和大于目标和或遍历完所有元素,则此路径不可行if current_sum > target or index == len(nums):return False# 尝试两种情况:将当前元素加入子集或不加入return dfs(index + 1, current_sum + nums[index]) or dfs(index + 1, current_sum)# 从第一个元素开始,当前子集总和为0return dfs(0, 0)