1. 归并排序

归并排序是一种效率仅次于快速排序的排序算法。它有非递归和递归两种实现方式(本文只讲述递归实现，非递归实现以后有专门的文章)。

其实，归并排序也叫外排序。它不仅可以对内存中的数据进行排序，还能对文件里的数据排序。

比如：假设有10G的数据放在硬盘的文件中，要排序，如何排呢？
我们知道，内存里的空间远远没有10G，假设有1G内存可用。首先我们可以把10G的文件切分成10个1G的文件，再依次读文件，每次把1G的数据读入内存的数组中，接着利用快排对其进行排序，再把排好序的那1G的数据写到硬盘的一个文件，再继续读下一个1G的数据……当10个文件里的数据都分别有序时，再利用归并排序进行两两归并，最终使10G的数据有序。

1.算法思想：

归并排序采用分治法。首先假设一组数据的左半区间有序，右半区间有序，将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

若将两个有序表合并成一个有序表，称为二路归并。

所谓 归并，就是将两组有序的数据合成为一组有序的数据。 例如有如下两个有序数组，将两个有序数组归并为一个有序数组，这就是一次归并操作。

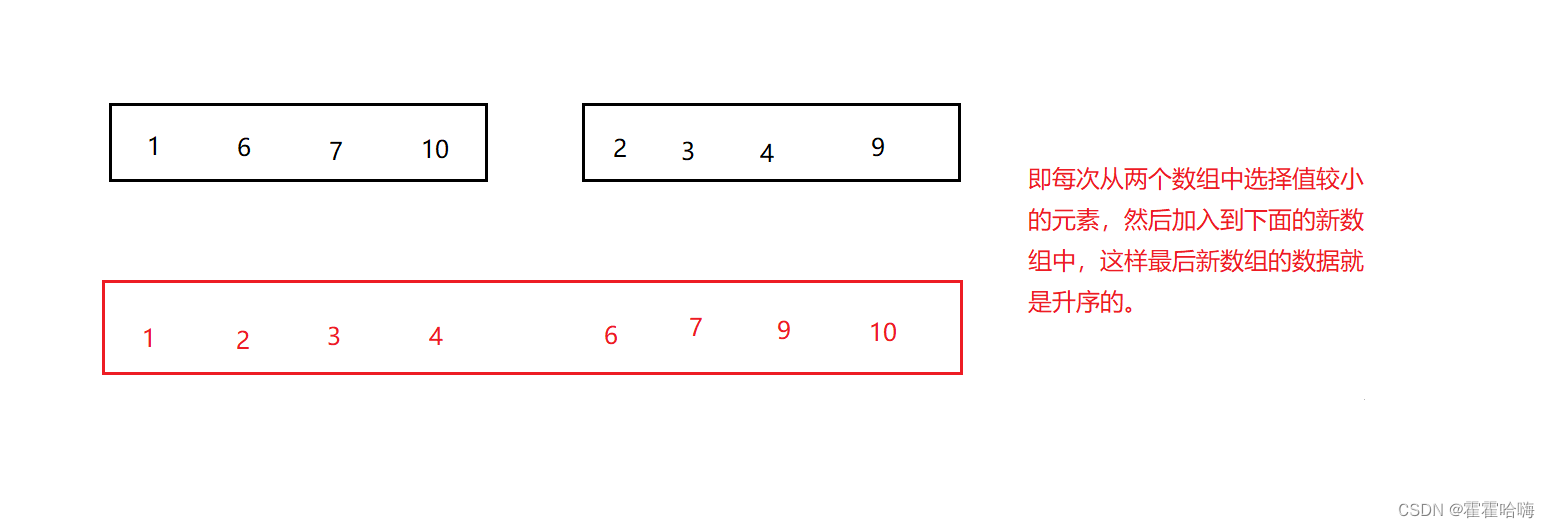
2.归并操作的工作原理如下：

第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。

第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置。

第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。

重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。

归并排序类似于二叉树的后序遍历，即先将左右的区间都排为有序后，然后才开始进行归并操作，因为归并必须要满足两个数组是有序的。

例如有如下数组。需要先将该数组每次都分割为两个区间，直到最后每个区间都只有一个值，此时比较两个值大小，然后将该两个值归并到一个数组中，此时就得到一个有两个元素的有序数组，然后再与另一个有两个元素的有序数组进行归并，然后就得到了一个有四个元素的有序数组，然后再与另一个有四个元素的有序数组进行归并，就得到了一个有八个元素的有序数组。就这样依次递归归并，直到最后目标数组为有序数组。

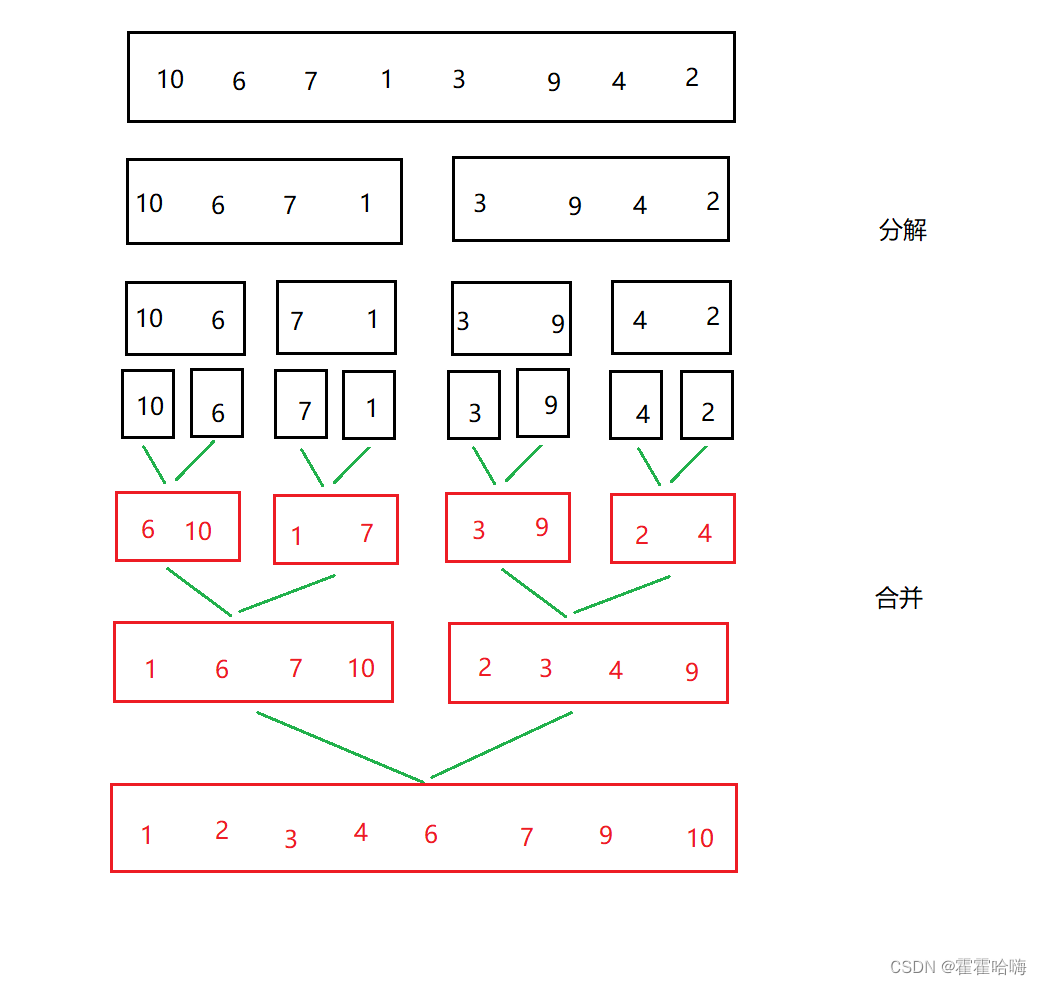
3.归并排序的代码实现如下：

//把数组分成区间
void _MergrSort(int* arr,int left,int right,int* tmp)
{//当左右两个区间只有一个元素或是不存在区间时，递归结束if (left >= right)return ;//右移1位右除以2的效果，用来把数组分成两个区间int mid = (left + right) >> 1;//假设[left mid] [mid+1 right]有序，就可以归并_MergrSort(arr, left, mid, tmp);_MergrSort(arr, mid + 1, right, tmp);//每次归并的过程int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}//当其中有一个区间结束时，另一个有序区间的数据直接拷贝进临时数组里while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}//最后把临时数组里面的数据拷贝回原数组for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}void MergrSort(int* arr, int sz)
{//创建临时数组存放数据int* tmp = (int*)malloc(sizeof(int) * sz);if (tmp == NULL){perror("malloc");return;}_MergrSort(arr, 0, sz - 1, tmp);free(tmp);tmp = NULL;
}

排序结果如下：

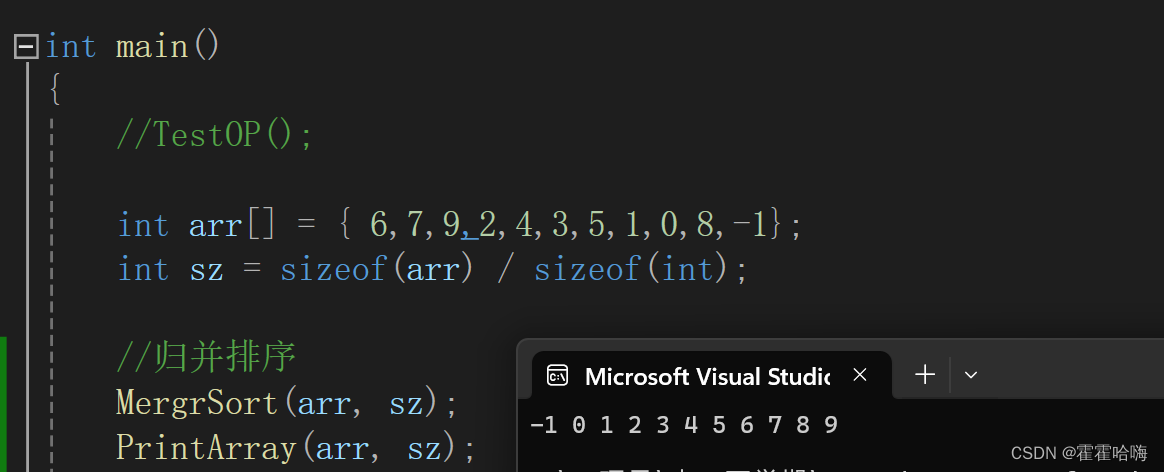
4.归并排序的时间复杂度和稳定性分析：

1.归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

2. 计数排序

计数排序是一种非比较排序，即不需要直接比较数据之间的大小来进行排序。

1.算法思想：

计数排序，是通过统计每一个数字出现的次数，并把它映射到与它自己本身数值相同的下标处，再遍历映射的数组使原数组有序的一种排序方法。

计数排序的本质是一种哈希算法，也就是通过建立映射关系来达到排序的目的。

2.映射过程的图解如下：

基本思路：

先开辟一个映射数组，然后遍历原数组，数组中的元素是几就在开辟的的映射数组下标为几的位置+1，得到的这个映射数组就包含了原数组中所有元素的映射关系，最后遍历一遍映射数组找出原数组中出现过的数即可。

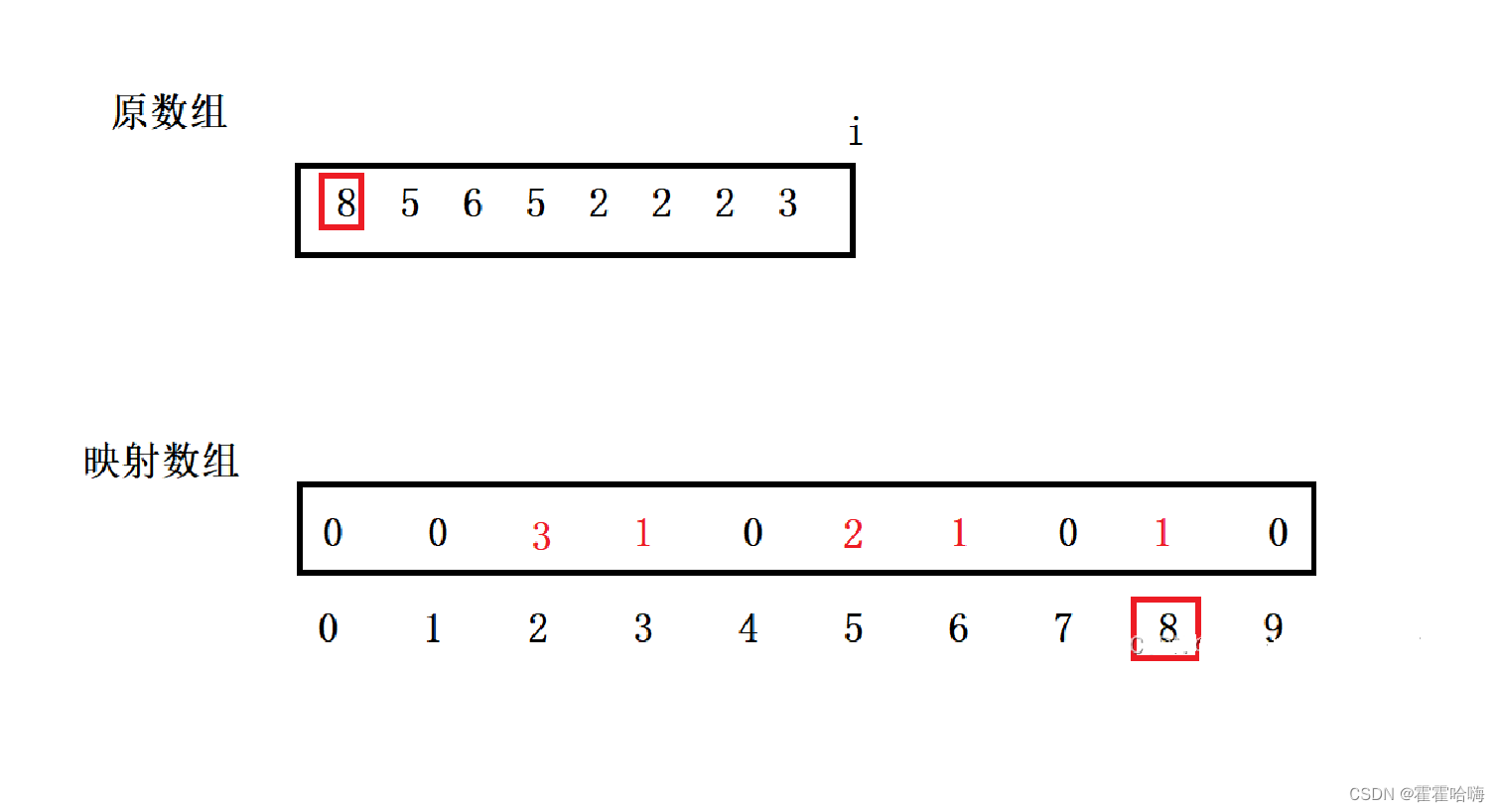
如图所示，原数组中有一个8，那么在映射数组的下标为8的位置记为1；原数组中有两个5，在映射数组的下标为5的位置记为2……以此类推。

但是这样映射也面临着一个问题，那就是我们开辟的数组到底要开多大的空间呢？ 显然，我们在上述例子中开辟了10个整形空间的数组，但是可以看到，有5个位置都是空的，也就是说有五个位置的数都是没出现过的，这样子开辟空间显然是有些浪费了，我们上面的写法是一种绝对映射的写法，绝对映射就是这个数本身是多少就映射到下标为多少的位置，但是如果我给出以下这个数组让你排序呢？

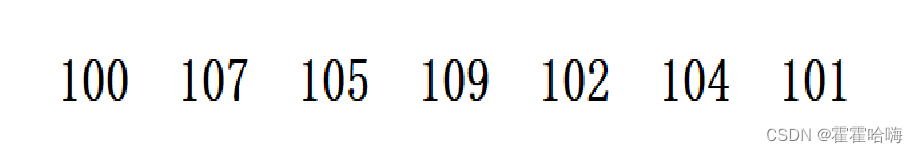
显然，以上数字的最大值是109，也就是说如果用绝对映射的方法那我们至少需要开110个空间，因为109要映射到下标为109的位置，下标从0开始，0-109就是110个数。但是仔细观察你会发现，这些数都是在100-109之间的，换句话说如果你开辟110个空间，那么前100个位置都是0，没有数映射，所以就等于是白白浪费了100个整形的空间，这显然是不能接受的。

所以有人就想出来了一种相对映射的方法，把100映射到0的位置，把109映射到9的位置，其它的也以此类推，每个数在映射的时候都减去100，等到取出数据的时候在加上100就能得到原来的数了。这样一来，我们需要开10个整形的空间就可以了，大大减少了内存的消耗。

那么真正开辟的空间该如何计算呢？

开辟的空间的大小=最大元素-最小元素+1
例如上面的例子就是：开辟空间的大小=109-100+1=10
为什么要+1？因为数组下标是从0开始的，如果不+1，那就是开辟9个空间，那么109就没法映射到109-100=9的位置了。

3.计数排序的代码实现如下：

void CountSort(int* arr, int sz)
{int max = arr[0];int min = arr[0];//找出最大值和最小值for (int i = 0; i < sz; i++){if (arr[i] > max){max = arr[i];}if (arr[i] < min){min = arr[i];}}//求出范围，就是要开辟的空间的大小int range = max - min + 1; int* count = (int *)calloc(range, sizeof(int)*range);if (count == NULL){perror("calloc fail!\n");return;}//统计每个数字出现的次数，相对映射到开辟的数组中for (int i = 0; i < sz; i++){count[arr[i] - min]++;}//把数据进行排序，放回原数组中int j = 0;for (int i = 0; i < range; i++){while (count[i]--){//后置++，先用后加arr[j++] = i + min;}}free(count);count = NULL;}

排序结果如下：

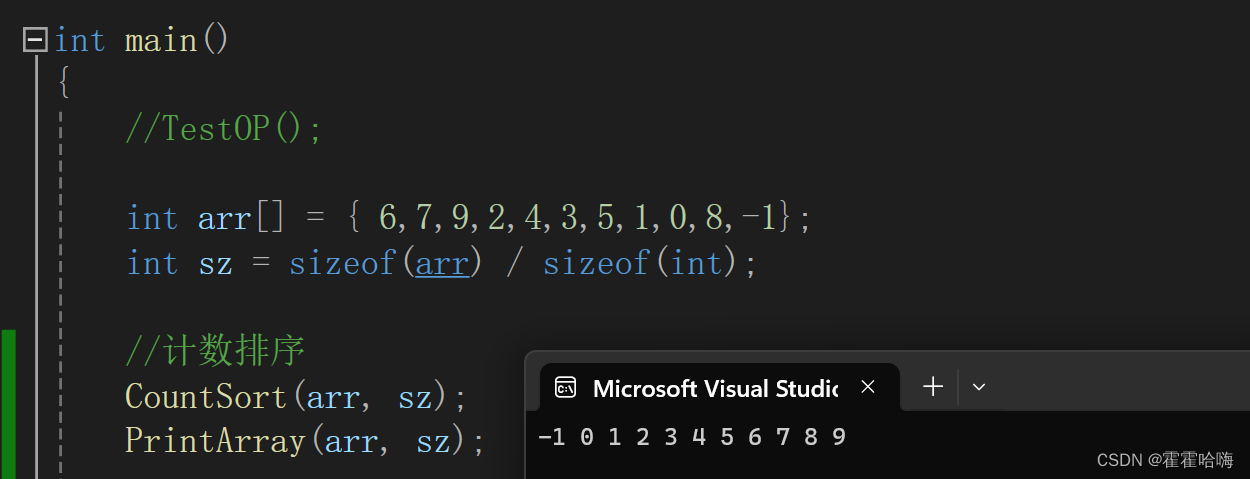
4.归并排序的时间复杂度和稳定性分析：

1.计数排序的局限性在于它更加适用于范围集中的一组整型数据的排序，这时效率非常高，如果数据的范围较大(就是代码中的 range )，或是排序其他类型的数据，就可能不太适用。
2.时间复杂度：O(N+range)
3.空间复杂度：O(range)
4.稳定性：稳定