1鸢尾花分类
鸢尾花分类问题是一个经典的机器学习问题,旨在根据鸢尾花的花萼长度、花萼宽度、花瓣长度和花瓣宽度等特征,将鸢尾花分成三个品种:山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。
这个问题常用的解决方法是使用机器学习算法来构建一个分类器,然后使用该分类器对新的鸢尾花样本进行分类。常用的分类算法包括支持向量机(SVM)、K近邻(K-Nearest Neighbors)、决策树(Decision Tree)等。
在解决鸢尾花分类问题时,通常采取以下步骤:
-
数据获取与准备: 首先,需要收集包含鸢尾花样本的数据集,常用的是经典的鸢尾花数据集,例如
iris数据集。然后,对数据进行预处理,包括数据清洗、特征选择、特征缩放等。 -
选择模型: 选择适合问题的分类模型,常见的包括支持向量机(SVM)、K近邻(K-Nearest Neighbors)、决策树(Decision Tree)、随机森林(Random Forest)等。
-
训练模型: 使用训练数据对选择的模型进行训练,这一过程会使模型根据数据学习到相应的规律或模式。
-
模型评估: 使用测试数据评估模型的性能,通常使用准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值等指标来评估模型的表现。
-
模型调优: 根据评估结果,对模型进行调优,例如调整模型的超参数、选择更合适的特征等,以提高模型的性能。
-
模型应用: 最终,将训练好的模型用于实际问题中,对新的鸢尾花样本进行分类预测。
题目描述:
要求: 鸢尾花分类问题,我们可以通过python的sklearn库,给出预测结果和实际值的对比,并且给出正确率评分。
- 1、导入sklearn库,包括需要用到的数据集dataset.load_iris()、svm分类器工具和、模型用到的数据集拆分工具。
- 2、使用python命令导入数据,并且设置好训练集和测试集。
- 3、创建svm.LinearSVC分类器
- 4、使用分类器clf的fit方法进行拟合训练
- 5、使用分类器clf的predict方法对测试集数据进行预测
- 6、对比测试集的预测结果和测试集的真实结果,并且使用clf的score方法获得预测准确率。
代码:
from sklearn import datasets # 导入数据集模块
from sklearn import svm # 导入支持向量机模块
from sklearn.model_selection import train_test_split # 导入数据集拆分工具
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征数据
y = iris.target # 类别标签
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
# 创建线性支持向量机分类器
clf = svm.LinearSVC()
# 使用训练集训练分类器
clf.fit(X_train, y_train)
# 对测试集进行预测
y_predict = clf.predict(X_test)
# 对比预测结果和真实结果,并输出
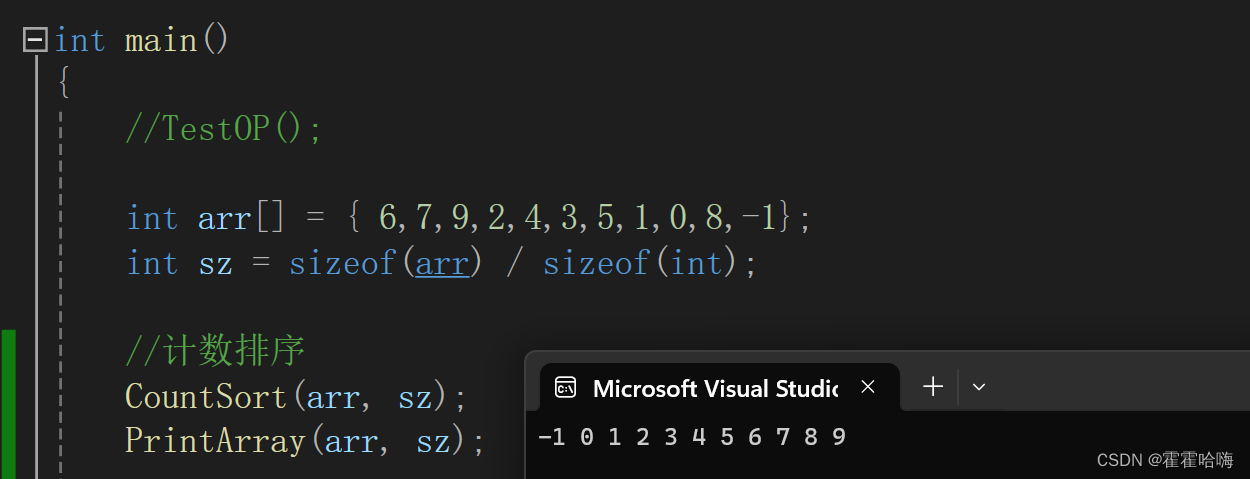
comparison = ['预测值: ' + str(a) + ' 实际类别: ' + str(b) for a, b in zip(y_predict, y_test)]
for comp in comparison:print(comp)
# 输出分类器在测试集上的准确率
print(f'准确率:{clf.score(X_test, y_test)}') 结果如图:
2 KNN算法
K近邻(K-Nearest Neighbors,KNN)算法是一种基本的分类和回归方法。其基本思想是:对于新的样本数据,通过计算其与训练集中的样本的距离,然后选取距离最近的K个样本,根据这K个样本的类别(对于分类问题)或者值(对于回归问题),通过多数表决或者加权平均的方式确定新样本的类别或者值。
在KNN算法中,K是一个用户定义的常数,表示选择最近邻的数量。K的选择会直接影响到算法的性能,一般来说,K值越小,模型对噪声和孤立点的敏感度越高,而K值越大,模型的平滑程度越高,但也可能导致模型欠拟合。
KNN算法不需要显式的训练过程,而是将训练集中的数据保存起来,当需要对新的样本进行预测时,直接在保存的数据集中进行搜索和计算。因此,KNN算法是一种懒惰学习(lazy learning)算法。
KNN算法的优点包括简单易懂、易于实现以及在训练集较大的情况下表现良好。然而,KNN算法的缺点也很明显,主要包括对数据集的高度依赖、计算复杂度高、对于高维数据和大规模数据集的效率低下等。
题目描述:
使用K近邻算法,构建一个预测鸢尾花种类的模型。
要求
- 加载鸢尾花数据集
- 对数据集进行划分:参数test_size=0.2,random_state=2
- 构建KNN模型:调用sklearn中的函数进行构建
- 训练模型
- 预测模型:选取测试集中的第3组数据(下标为2)进行预测
- 输出得到的预测值和真实值
代码:
from sklearn import datasets # 导入数据集模块# 加载鸢尾花数据集
iris = datasets.load_iris()
x = iris.data # 特征数据
y = iris.target # 类别标签# 划分数据集
from sklearn.model_selection import train_test_split
# 将数据集划分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=2)# 构建模型
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3) # 使用K近邻算法,设置邻居数为3# 训练模型
knn.fit(x_train, y_train)# 模型预测
x_to_predict = x_test[2].reshape(1, -1) # 选取测试集中的第3组数据(下标为2)进行预测
y_predicted = knn.predict(x_to_predict)# 输出预测值和真实值
print("预测值:" + str(y_predicted)) # 输出预测的类别
print("真实值:" + str(y_test[2])) # 输出该样本在测试集中的真实类别结果如图:
3策树分类模型
决策树是一种基于树状结构的监督学习算法,用于解决分类和回归问题。在决策树中,每个内部节点表示一个特征属性上的判断条件,每个分支代表一个判断结果,每个叶子节点表示最终的分类结果或数值预测结果。
决策树的构建过程是一个递归地选择最佳特征进行分裂的过程,直到满足停止条件为止。在构建决策树时,一般会使用信息增益、基尼不纯度等指标来选择最佳的特征进行分裂,以使得每次分裂后的数据集更加纯净(即同一类别的样本更加集中)。
以下是决策树分类的一些重要知识点:
-
节点与叶子节点:决策树由节点和叶子节点组成。节点表示一个特征属性上的判断条件,叶子节点表示最终的分类结果。
-
分裂准则:在构建决策树时,需要确定节点分裂的准则。常用的准则包括信息增益、基尼不纯度等,用于选择最佳的特征进行分裂。
-
剪枝:为了避免过拟合,决策树需要进行剪枝操作。剪枝可以分为预剪枝(在构建树的过程中进行剪枝)和后剪枝(在构建完整棵树后再进行剪枝)。
-
特征选择:在每个节点上,需要选择最佳的特征进行分裂。常用的特征选择方法有信息增益、基尼指数、方差等。
-
决策树的优缺点:
- 优点:易于理解和解释,可视化效果好,能够处理数值型和类别型数据,对缺失值不敏感。
- 缺点:容易过拟合,对噪声数据敏感,不稳定,需要进行剪枝操作。
-
集成学习中的应用:决策树常被用于集成学习方法中,如随机森林和梯度提升树。这些方法通过组合多个决策树来提高分类准确率和泛化能力。
题目描述:
对红酒数据集创建决策树分类模型,并输出每个特征的评分。
要求
- 从sklearn的datasets模块中导入load_wine 包,读取红酒数据集,
- 转换为DataFrame格式,将数据集划分为特征样本和标签样本,
- 使用该数据集建立决策树分类模型,树深设置为5,随机种子设置为1,其他值设置为默认值
- 将数据放入模型中进行训练,要求输出每个特征的评分。
代码:
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_wine# 加载红酒数据集
wine = load_wine()# 创建DataFrame格式的特征样本和标签样本
x_train = pd.DataFrame(data=wine["data"], columns=wine["feature_names"]) # 特征样本
y_train = wine["target"] # 标签样本# 建立决策树分类模型
model = DecisionTreeClassifier(max_depth=5, random_state=1)
model.fit(x_train, y_train) # 模型训练# 输出每个特征的评分(特征重要性)
print("每个特征的评分(特征重要性):")
for feature, importance in zip(wine["feature_names"], model.feature_importances_):print(f"{feature}:{importance:.4f}") # 对每个特征列进行评分