算法刷题Day28 | 93.复原IP地址、78.子集、90.子集II

0 引言

加油

1 复原IP地址

🎈 文档讲解
🎈 视频讲解
🎈 做题状态：

1.1 我的解题

其实就是切割问题，只不过需要考虑到 IP 的特殊性。就是要额外思考什么情况下切割的字符是满足情况的。

class Solution {
public:string combineIP(const vector<int>& path){string ip;for (auto data : path){ip += to_string(data);ip += '.';}ip.pop_back();  // 删除最后的 . return ip;}// 回溯函数void backTracing(string& s, int startIndex, vector<int>& path, vector<string>& paths){// 终止条件（注意path的长度只能是4）if (startIndex == s.size() && path.size() == 4){// 将path变换后插入res数组中paths.emplace_back(combineIP(path));}// 单层回溯逻辑for (int i = startIndex; i < s.size(); i++){string tmp = s.substr(startIndex, i - startIndex + 1);if (tmp.size() > 4){continue;}int number = stoi(tmp);// 如果条件不满足的话，就执行下一个分支，而不是跳出循环体if (number < 0 || number > 255 || (tmp.size() > 1 && tmp[0] == '0') ){continue;}// 条件满足path.emplace_back(number);backTracing(s, i + 1, path, paths);path.pop_back();}}vector<string> restoreIpAddresses(string s) {vector<int> path;vector<string> paths;backTracing(s, 0, path, paths);return paths;}
};

2 子集

🎈 文档讲解
🎈 视频讲解
🎈 做题状态：秒杀了

2.1 我的解题

这道题其实和前面的组合问题，只是将 path 添加到 paths 结果集中的时机不同。组合问题是将满足条件的叶子节点添加到 paths 中，然后子集则是将所有节点都添加到 paths 中。

#include <iostream>
#include <vector>
#include <algorithm>class Solution {
public:void backTracing(vector<int>& nums, int startIndex, vector<int>& path, vector<vector<int>>& paths){// 结束条件if (startIndex == nums.size()){return;}for (int i = startIndex; i < nums.size(); i++){path.emplace_back(nums[i]);paths.emplace_back(path);backTracing(nums, i + 1, path, paths);path.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {vector<int> path;vector<vector<int>> paths;paths.push_back({});backTracing(nums, 0, path, paths);return paths;}
};

3 子集II

🎈 文档讲解
🎈 视频讲解
🎈 做题状态：

3.1 我的解题

这道题和 40.组合总和II 类似，在给定的数组中都是有重复元素的，但是返回的子集中又不能有重复的元素。

这道题的关键就是树枝不用去重、树层去重。因为树层中，假如两个相邻节点以同样的数字开始遍历（假如都是从 1 开始），那么左侧的树枝已经将右侧树枝的结果已经组合完了。此时右侧再从这个数遍历的话就会发生重复了。所以要进行树层的去重。

树层如何去重呢？需要一个额外的数组记录每个数被使用的信息。当两个节点的值相等时，而且左侧节点的 used 数组为 false ，也就是没用过，表示这两个节点是同一个树层的关系。假如 used 数组为 true，表示这两个节点是同一个树枝的关系。
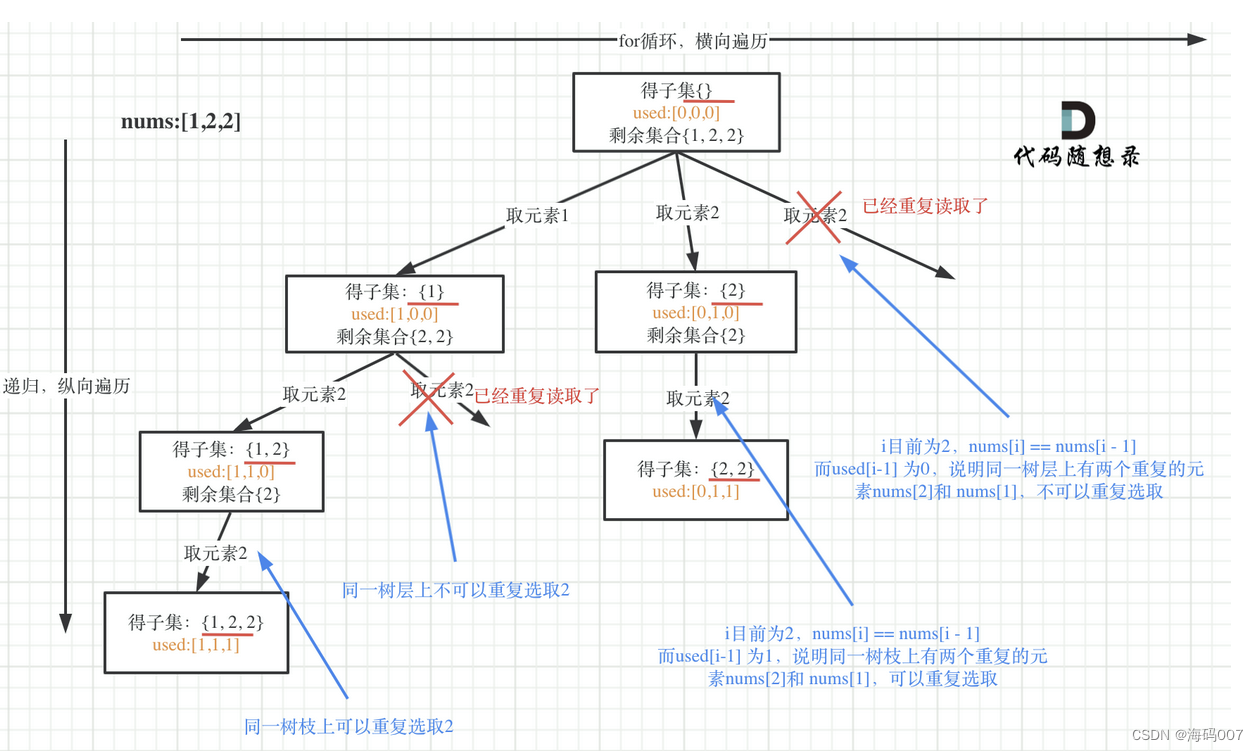
在这里插入图片描述

#include <algorithm>class Solution {
public:void backTracing(vector<int>& nums, int startIndex, vector<bool>& used, vector<int>& path, vector<vector<int>>& paths){paths.emplace_back(path);if (startIndex == nums.size()){return;}for (int i = startIndex; i < nums.size(); i++){// 判断是否要树层去重if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false){continue;}path.emplace_back(nums[i]);used[i] = true;backTracing(nums, i + 1, used, path, paths);path.pop_back();used[i] = false;}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());vector<bool> used(nums.size(), false);vector<int> path;vector<vector<int>> paths;backTracing(nums, 0, used, path, paths);return paths;}
};