简单题之数字总结

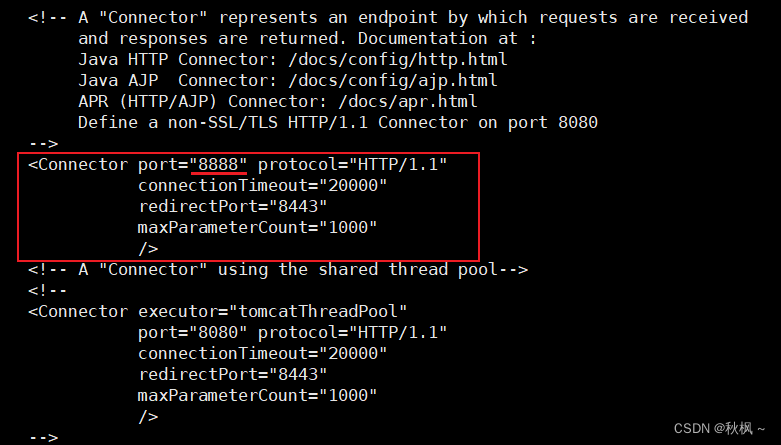
1.求数的幂

考点：二分幂（快速幂）的应用
思路：
直接暴力会超时，因此我们考虑用递归实现
如何用递归实现？
二分幂:对我们的幂次数分情况考虑：
1.M=0，return 1;
2.M为奇数时，即M%2！=0，底数不断累乘取模
3.否则，M为偶数，对其折半转成奇数，累乘取模
在这里插入图片描述

#include <iostream>
using namespace std;
const int maxn=1e5+10;
long long  n,N,M,P;
int res[maxn];//  如何用递归实现？
//N,M,P数比较大，考虑用Long型装
long long binary(long long a,long long b,long long c){// 1.M=0，return 1;if(b==0) return 1;// 2.M为奇数时，即M%2！=0，底数不断累乘取模else if(b%2!=0)return a*binary(a,b-1,c)%c;// 3.否则，M为偶数，对其折半转成奇数，累乘取模else return binary(a,b/2,c)*binary(a,b/2,c)%c;
}  int main()
{int len=0;// 直接暴力会超时，因此我们考虑用递归实现cin>>n;while(n--){cin>>N>>M>>P;res[len++]=binary(N,M,P);}for(int i=0;i<len;i++){cout<<res[i]<<endl;}return 0;
}

2.既约分数

考点：求最大公约数
思路：
1-2020最简分数:循环遍历是否其最大公约数即1：是个数++
求最大公约数
如何求最大公约数：辗转相除取余法-递归实现
两个数的最大公约数实质是由两者不断相除取模得到的：
比如25和5 :1.25%50 则此时最大公约数为5
比如22和2 :1.25%15!=0 t=25%15=10 再次对被除数对余数取模 t=a%t=5!=0 t=a%t==0 则此时最大公约数为5
在这里插入图片描述

#include <iostream>
using namespace std;// 求最大公约数
int is(int a,int b){if(b==0) return a;//返回最终余数-即最大公约数//否则不断除余数取模，并将结果保存在b中，b再次作为余数else return is(b,a%b);
}
int main()
{int sum=0;// 1-2020最简分数:循环遍历是否其最大公约数即==1：是 个数++ for(int i=1;i<=2020;i++){for(int j=1;j<=2020;j++){if(is(i,j)==1) sum++;}}cout<<sum;return 0;
}

进制转化

1.其它进制转化为十进制:
思路：
其它进制转化为十进制:当前位值*当前位的权值

如何获得当前位值？考虑可能很长，我们用一个字符串str存储，然后str-'0’转化为数字

如何计算当前的权值？第一位权值-1 第二位-进制数1 第三位-进制数进制数…

转换结果：sum+=当前位值*当前位权

在这里插入图片描述

#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main()
{string str="2022";int k=9,sum=0,base=1;for(int i=str.size()-1;i>=0;i--){// 用一个字符串str存储，然后str-'0'转化为数字int t=str[i]-'0';// 转换结果：sum+=当前位值*当前位权sum+=t*base;// 第一位权值-1 第二位-进制数*1 第三位-进制数*进制数...base*=k;}cout<<sum; return 0;
}

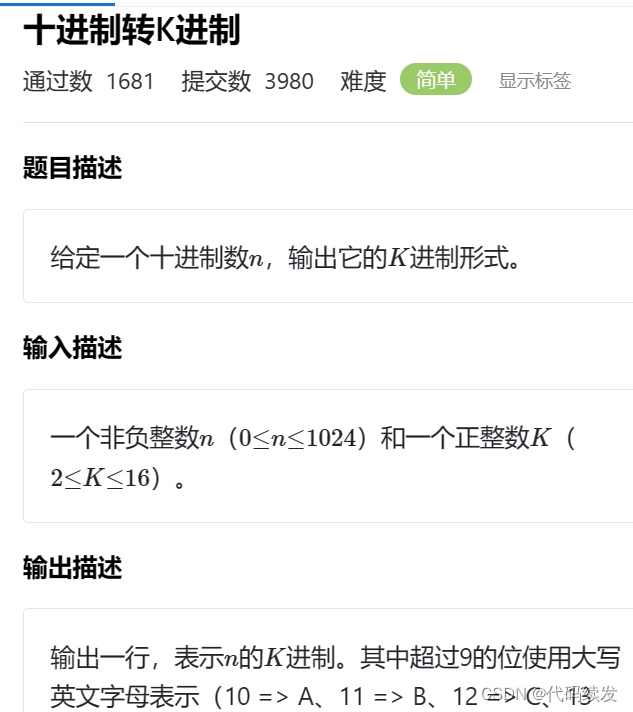
2.十进制转其它进制
思路：
如何将十进制转成其它进制？
以十进制转二进制为例：用十进制除2然后倒取余数法
2：2%2=0 2/2=1 取10 8%2=0 t=8/2=4%2=0 t=4/2=2%2=0 t=2/2=1 取1000
1.先模2存:由于要存储每一位的转换值，我们考虑用数组，但注意，最后取余数时，我们是倒序取的！！！
2.再判断除进制是否为0，是则结束
3.倒序输出
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;const int maxn=100;
int nu[maxn];
int main(){int n,k,len=0;cin>>n>>k;do{//先模2存:存储每一位的转换值nu[len++]=n%k;n/=k;}while(n);//判断除进制是否为0，是则结束// 倒序输出for(int i=len-1;i>=0;i--)if(nu[i]>9) cout<<(char)(nu[i]-10+'A');else cout<<nu[i];return 0;
}

X进制减法

思路：
求X进制下A-B的十进制结果最小值：

如何实现？
A-B在X进制下的值:AB对应数相减可得

再求每位数在合法条件下对应的最小进制数：由2开始
条件：每一数位上的数字<对应进制数，最小进制=数位+1 AB两个均要满足，则取AB中最大的数位

sum+=数位*最小进制数
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5;
const int m=1e9+7;
int n1[maxn],n2[maxn];
int n,a,b;
long long value,base=1,sum=0;
int main(){int n;cin>>n>>a;for(int i=a;i>=1;i--){cin>>n1[i];}cin>>b;for(int i=b;i>=1;i--){cin>>n2[i];}for(int i=1;i<=a||i<=b;i++){// 每一数位上的数字<对应进制数，最小进制=数位+1 AB两个均要满足，则取AB中最大的数位value=max(n1[i],n2[i])+1;// 再求每位数在合法条件下对应的最小进制数-2if(value<2) value=2;// sum+=数位*最小进制数sum=(sum+(n1[i]-n2[i])*base)%m;base=base*value%m;}cout<<sum%m;return 0;
}