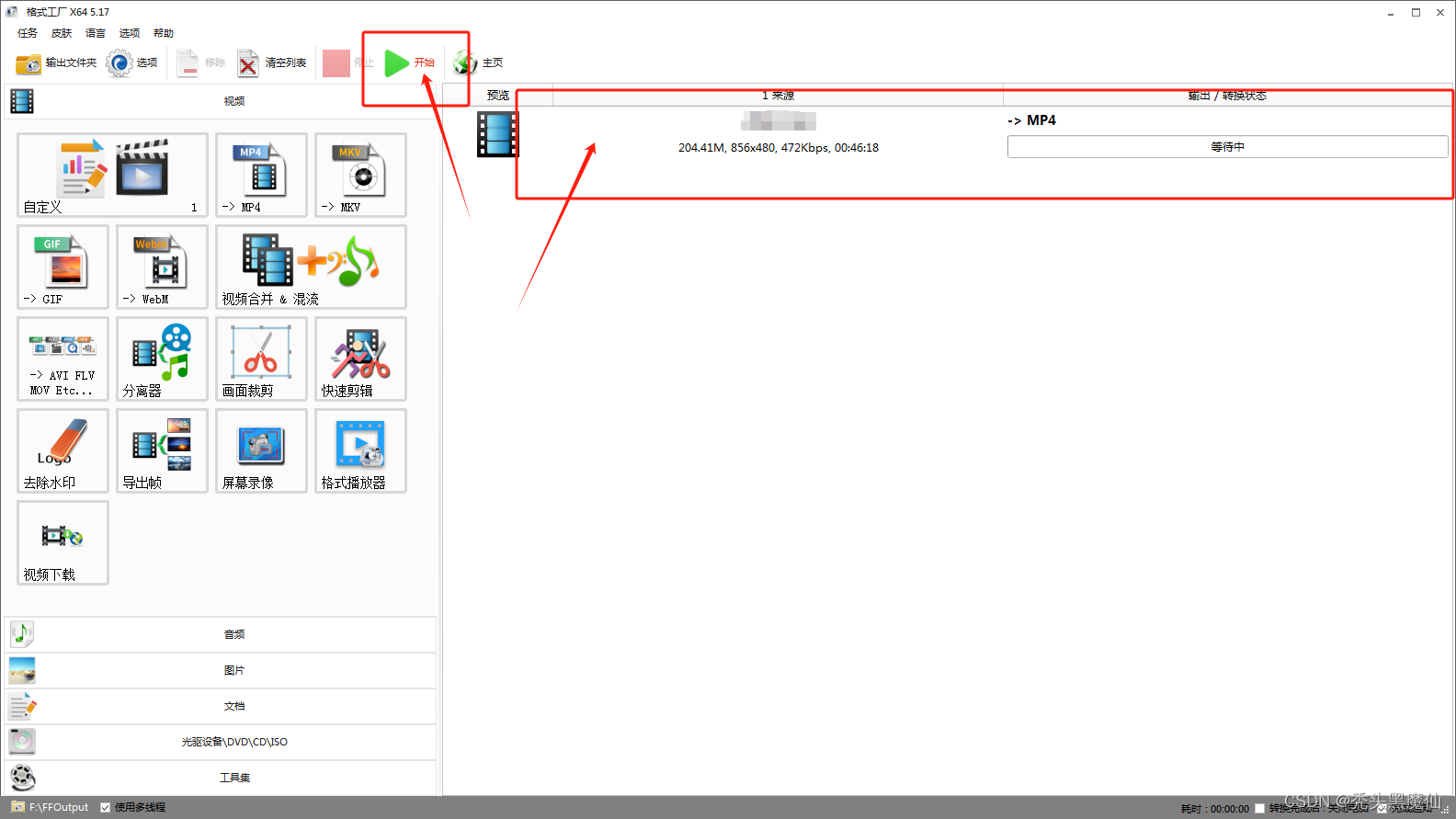
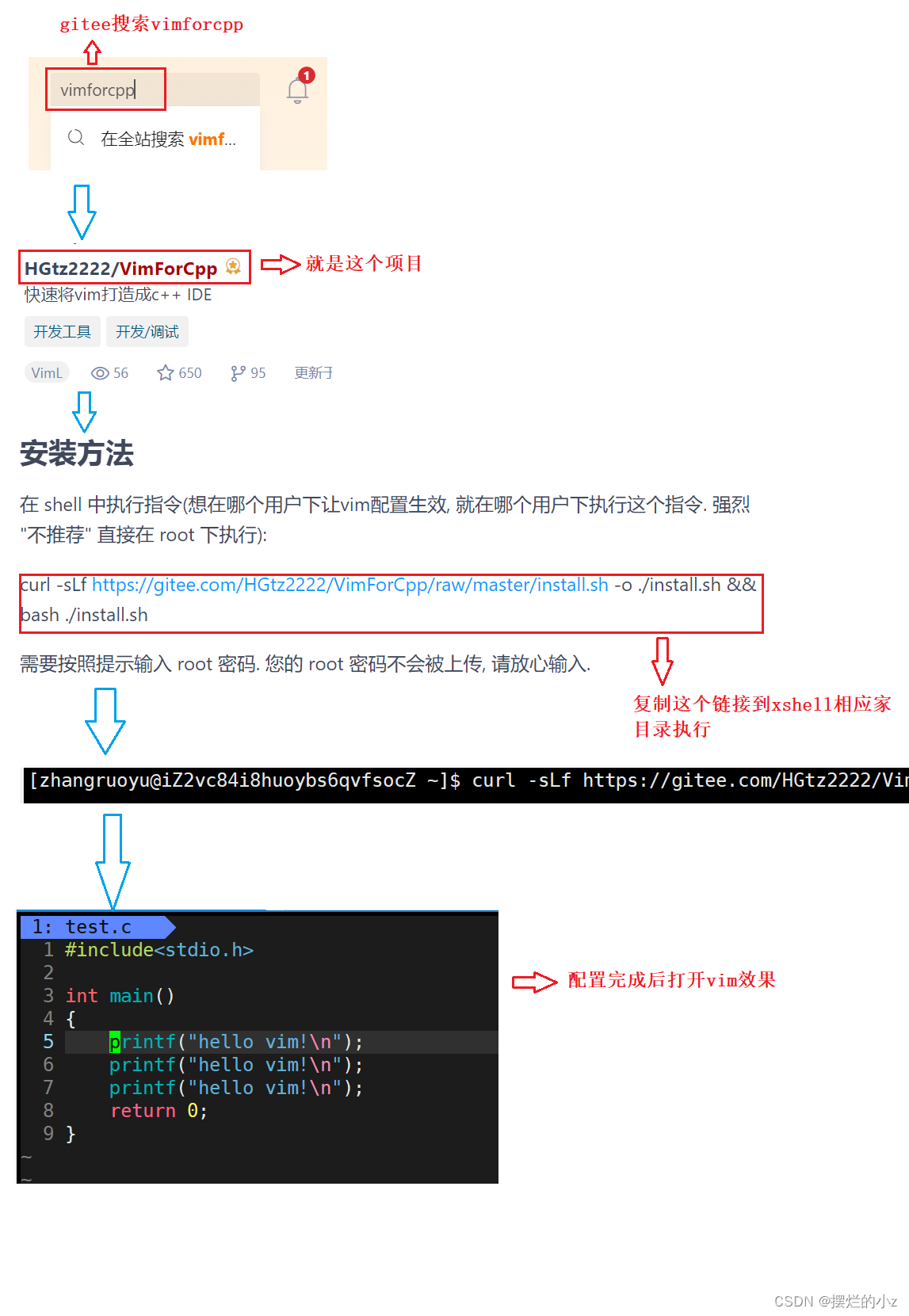
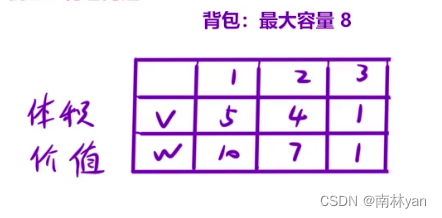
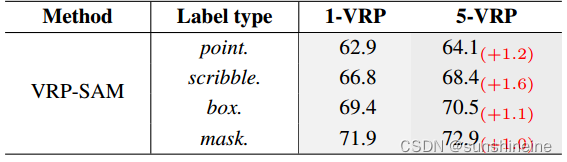
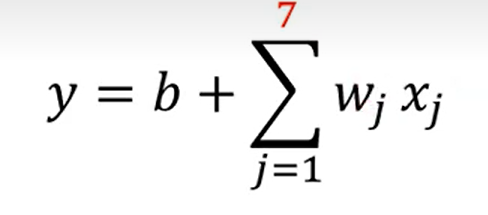机器学习和深度学习教程 – 李宏毅(笔记与个人理解)
day1
课程内容
- 什么是机器学习 找函数
- 关键技术(深度学习) 函数 – 类神经网络来表示 ;输入输出可以是 向量或者矩阵等
- 如何找到函数: supervised Learning 、 self supervised learning (pre train 又叫 Foundation Model 著名的例子有 Bert)、 Generative Adversarial Network、 Reforcement Learning
- 进阶内容 : Anomaly Detection 、 Explainable Al 、 Model Attack、 Domain Adaptation、NetWork Compression、 Life- Long learning 、 Meta Learning = learn to learn
Day2
introduction of Machine /deep Learning
Machine 是什么?
函数的不同类型
预测 分类
Structured learning 产生一个有结构的物件
一个例子 : Youtube Channel 的订阅量 找一个函数可以预测明天的观看次数
Step 1. y = w x1 +b Based on domain knowledge
Step 2. Define Loss From Training Data; Loss is a function of parameters L(b, w)
Step 3. Optimization w *, b * = arg min L ; Gradient Descent : 步长等于切线斜率(微分);然后还有一个n (ita)学习率来控制 w的变化长度 – > 通常自己设定hyperparameters
问题: 有可能陷入局部最优点; 可能的改进方法(self thinking)
1 取更好的初始点
2 改变学习率
3 找到所有的局部最优点(可以通过改变学习率进行跳出), 进行比较(例如找到十个不同的 局部最优点,然后进行min)
老师的伏笔: 高斯梯度 真正的痛点是什么?盲猜是 梯度消失 (wrong)
Gradient Descent
高斯梯度法的一般步骤: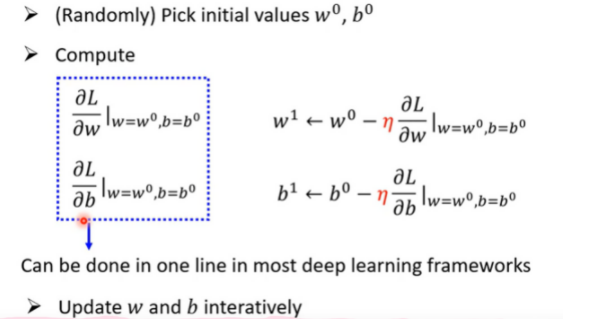
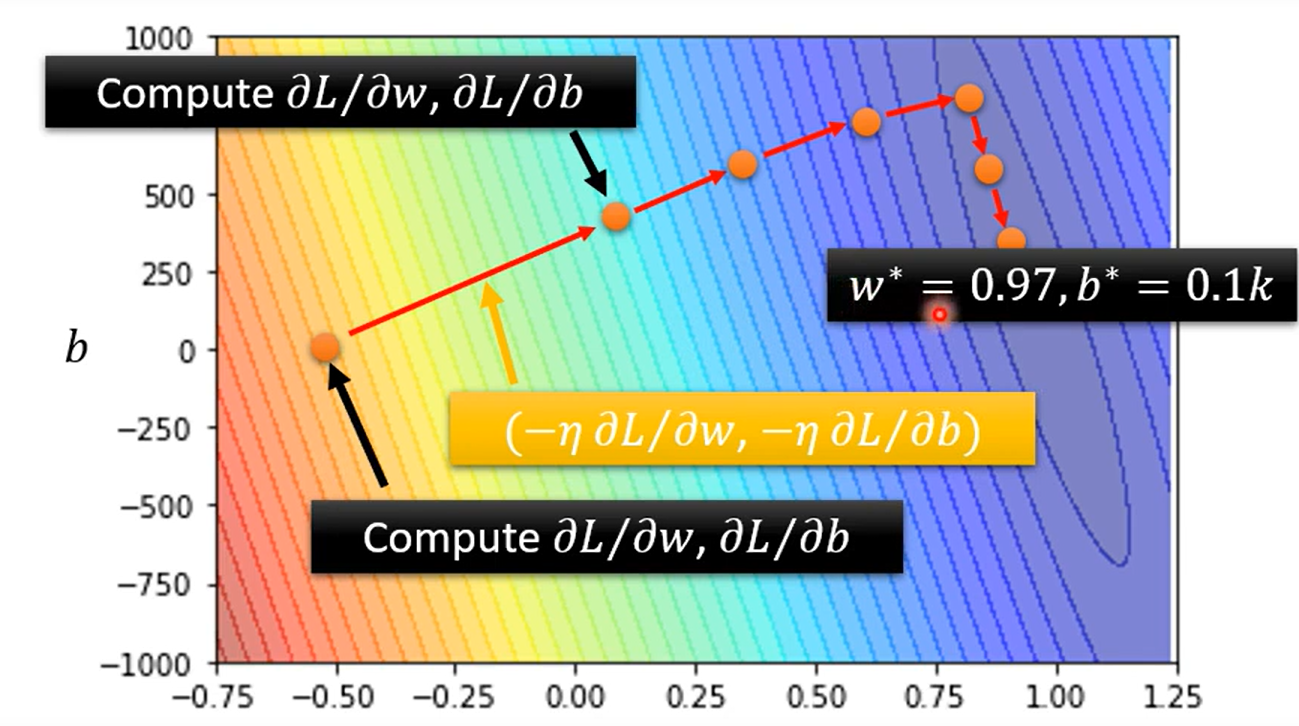
how to improve linear model?
因为 linear model 过于简单 造成了一定的 model bias; 需要有更多未知参数的model
如图所示 , 红色的线可以由 常数+ 一系列蓝色的线来拟合
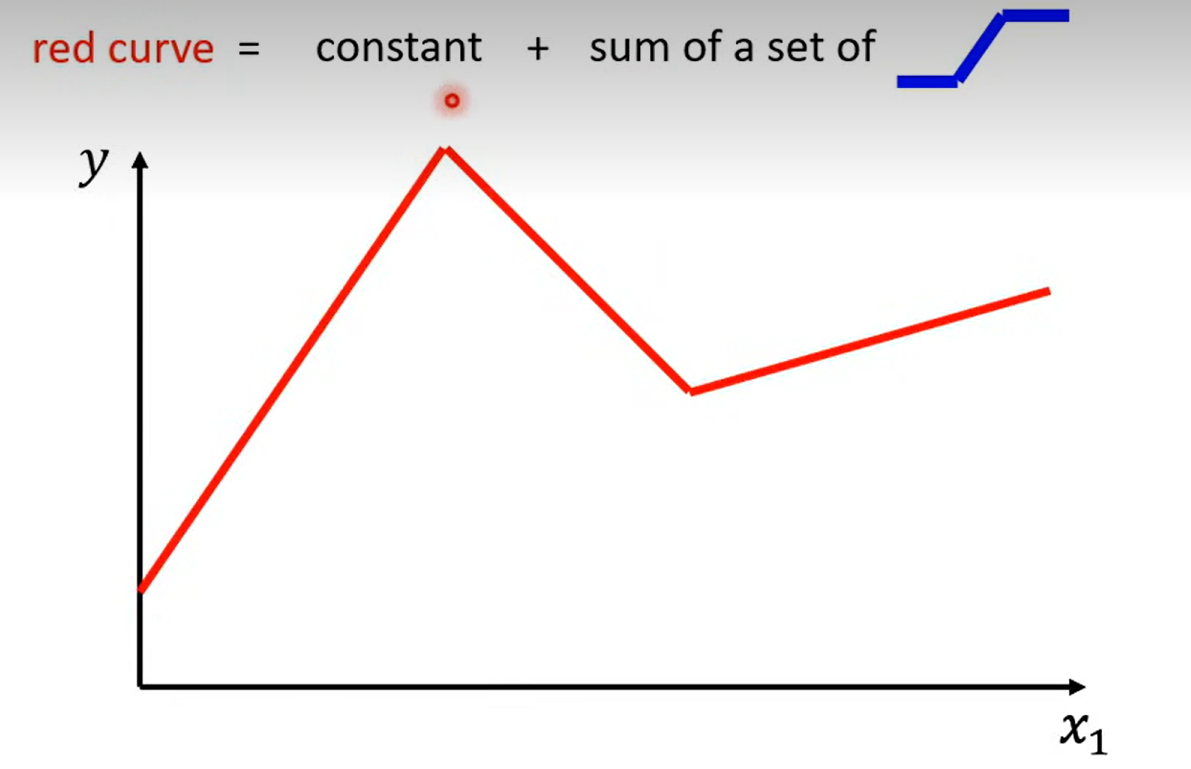
具体步骤如下:
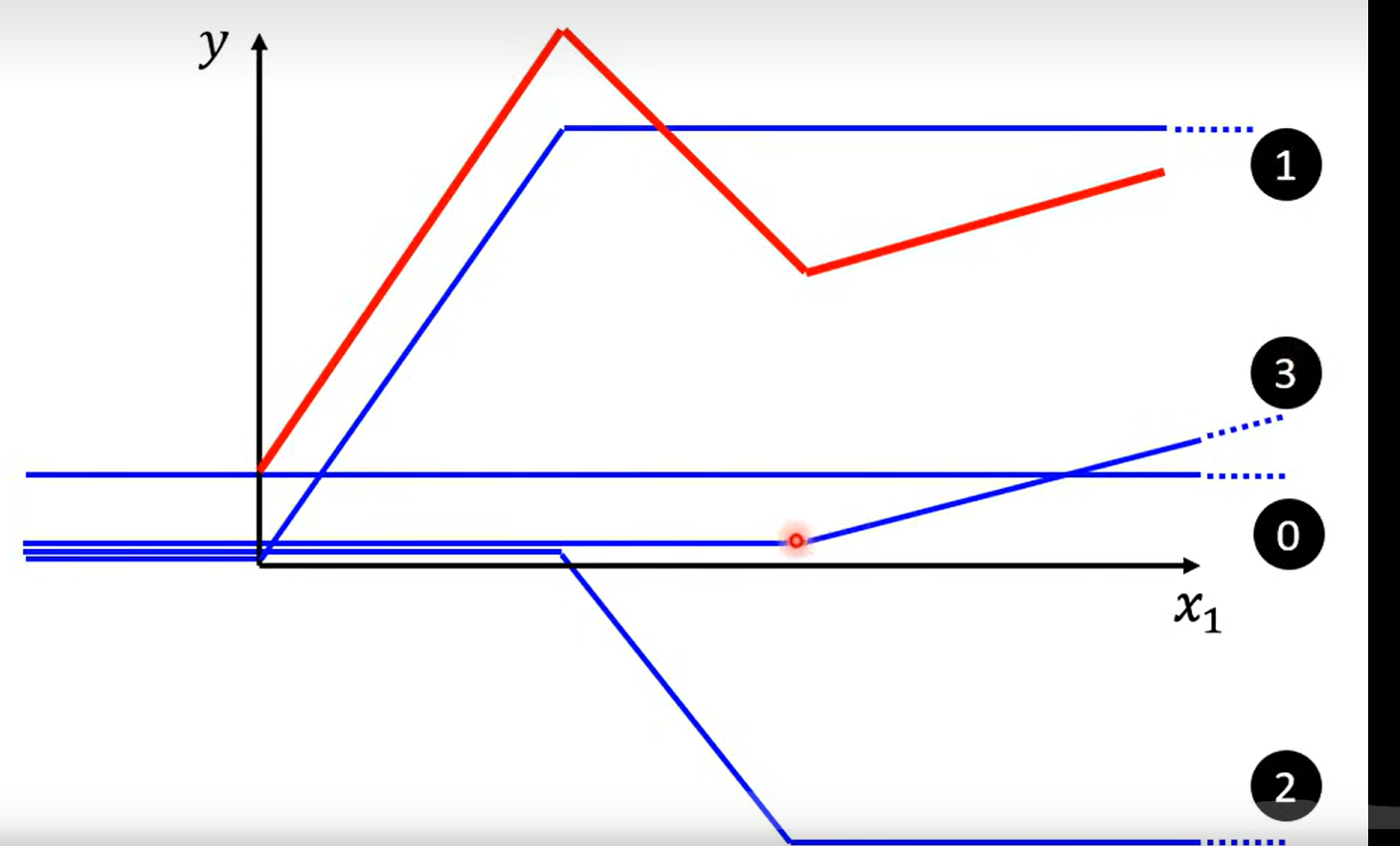
0+1+2+3 = red line
发现:
所有的piecewise linear curves 都可以由blue line 组成
发现 more:
beyond piecewise linear 也可以
how to represent this function (blue line )?
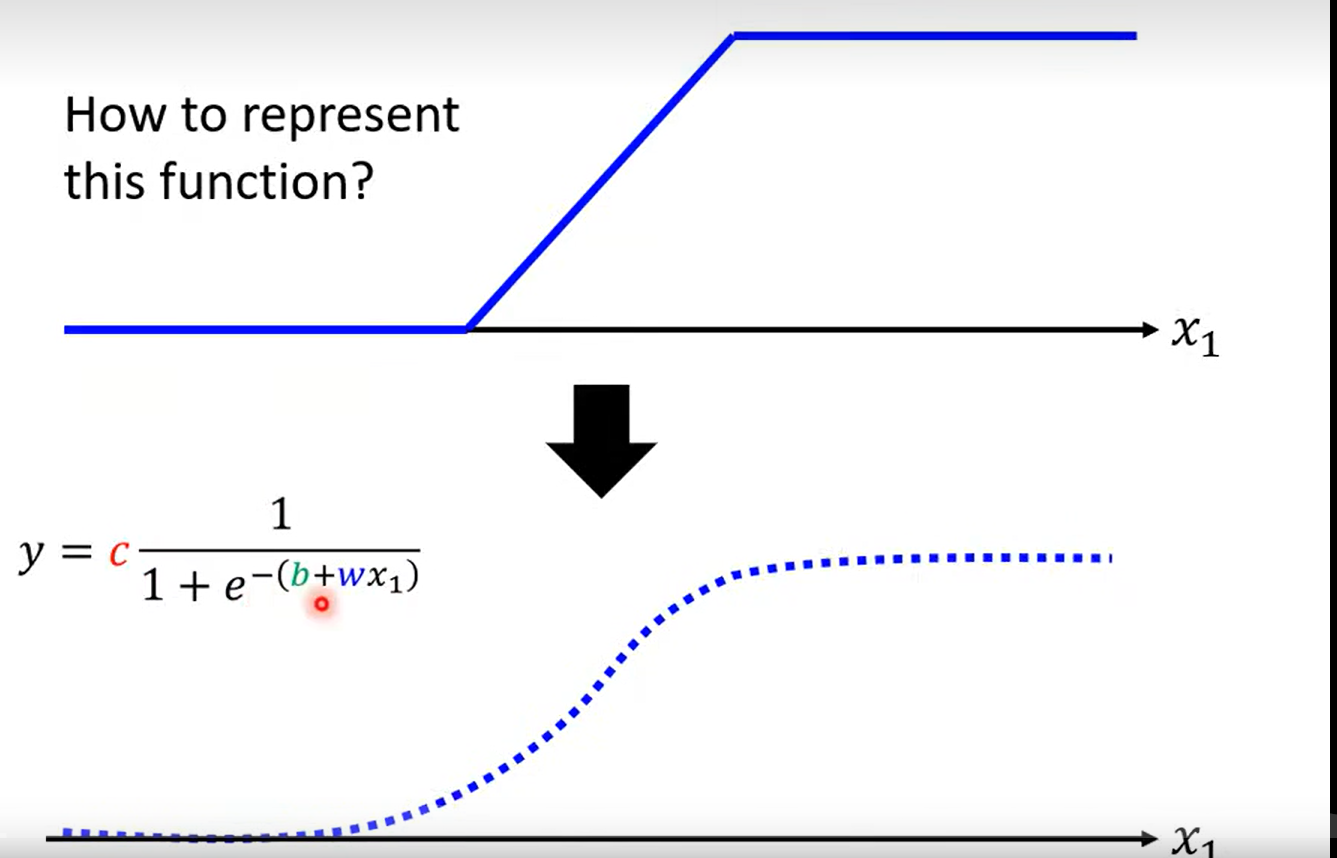
用一个近似的曲线表示 sigmoid function
more thinking:
- how to find the first sigmoid ? 数学变换?–> 人口增长的背景下,概率论中的伯努利分布 f(x|p)=px (1-p)1-x
- and w and b here 和 前面的linear functon 是否有关?无关
实际可用的拟合函数(折线函数)
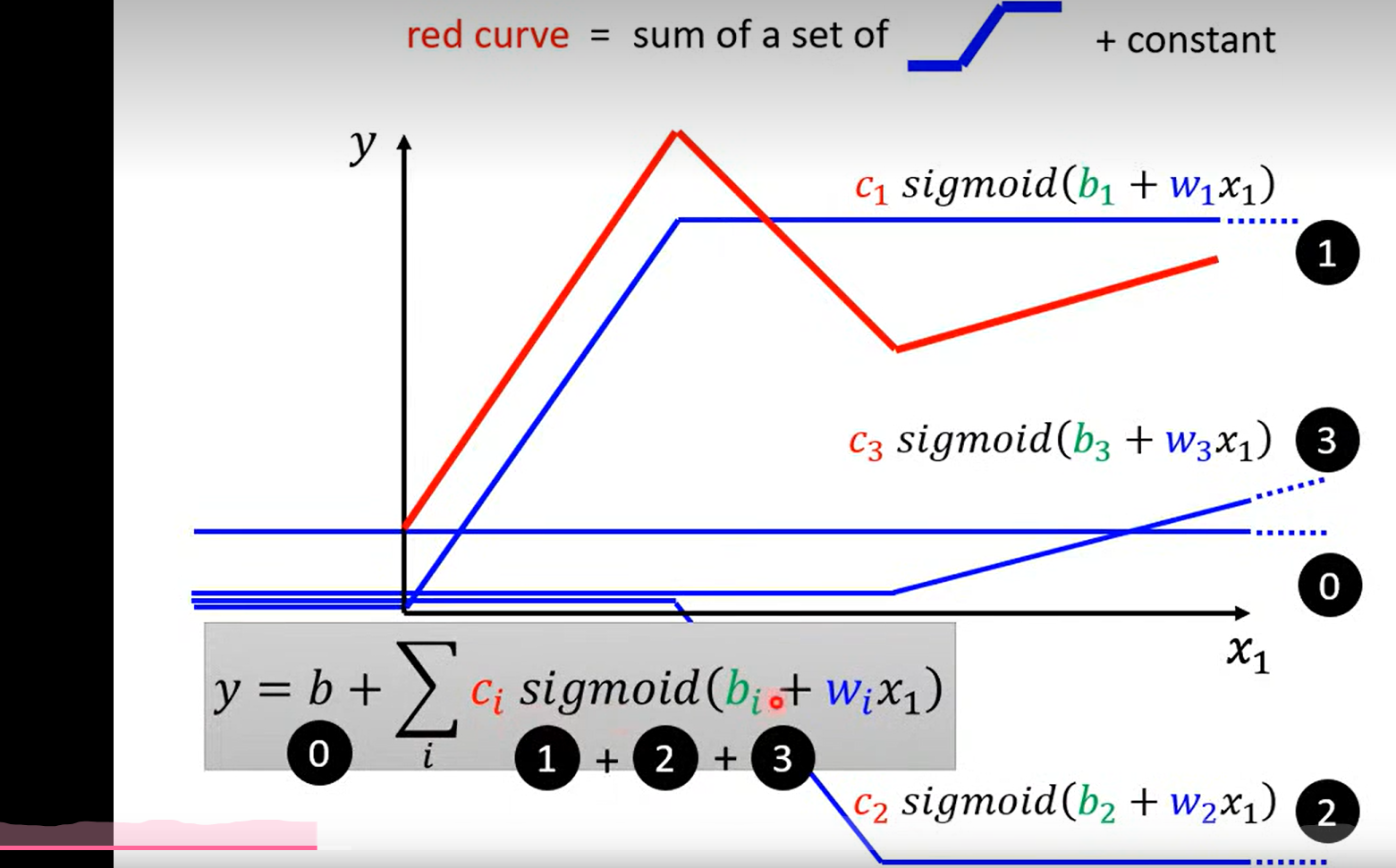
这里补充说明一点, 之前走了弯路, 以为这里的合成函数是一个分段函数, 后面的学习纠正过来, 这里就是单纯的 三个sigmoid 函数进行了 相加(有点多余, but who knows how could I say that )
NOw we have a new model which is more flexible
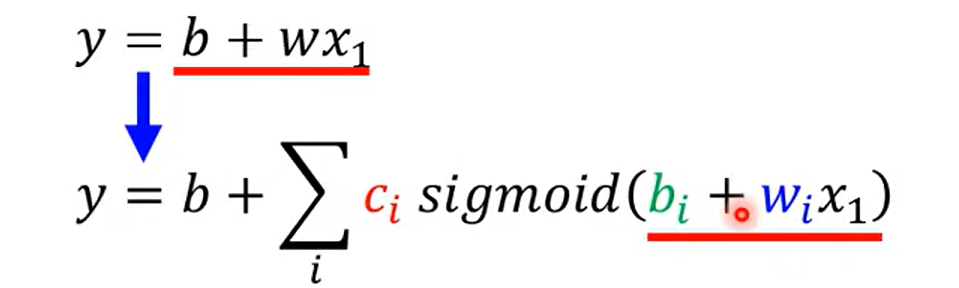
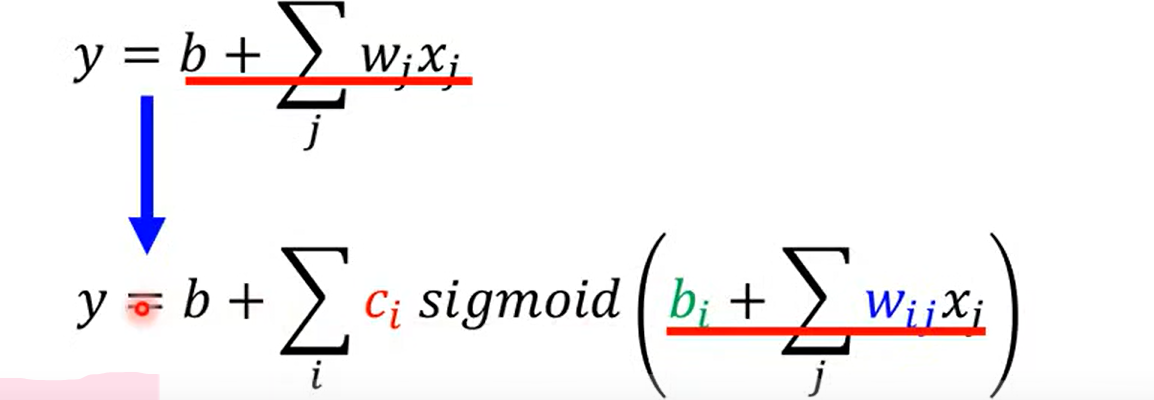
这里的w 表示特征,j表示特征的个数, 老师讲 如果是7天的话 j 就是1-7, 有一点点不明不白, 难道说之前的预测例子,是一个多特征的问题吗?
回忆, 好像确实和之前的linear model 有一点点不同, 一开始 取前一天,y = wx1 +b;后来取前七天的时候
注意这里的x 表示前j天的订阅次数, w 和b 是需要拟合的参数,也就是说这里至少需要拟合出7 组不同的w 一共有8 个参数(加上 b)。是根据前七天的订阅量, 预估第八天,相当于前七天是 不同的特征,预测第八天的特征,虽然老师这里的例子是实数值;换一个例子来表示可以这样理解: 选西瓜判断好坏瓜, 一开始只选择颜色(取值有 012 ),后来加上了 大小、响度,气味等不同的性状(取值为 0 1 2 ),然后预测瓜的取值(0 / 1 ); 从这个角度理解, 这个玩意儿相当于训练出 不同特征对于 结果影响的权重! nice
得出结论, 是的老师之前讲的例子确实相当于一个多特征的例子 √
言归正传, 那么这里老师讲得到一个 关于w 的参数矩阵, 和b,c 的参数向量,以及 最外面的b ;
那么接下来的问题就变成,优化 这些参数使得 L 最小 (nice!)
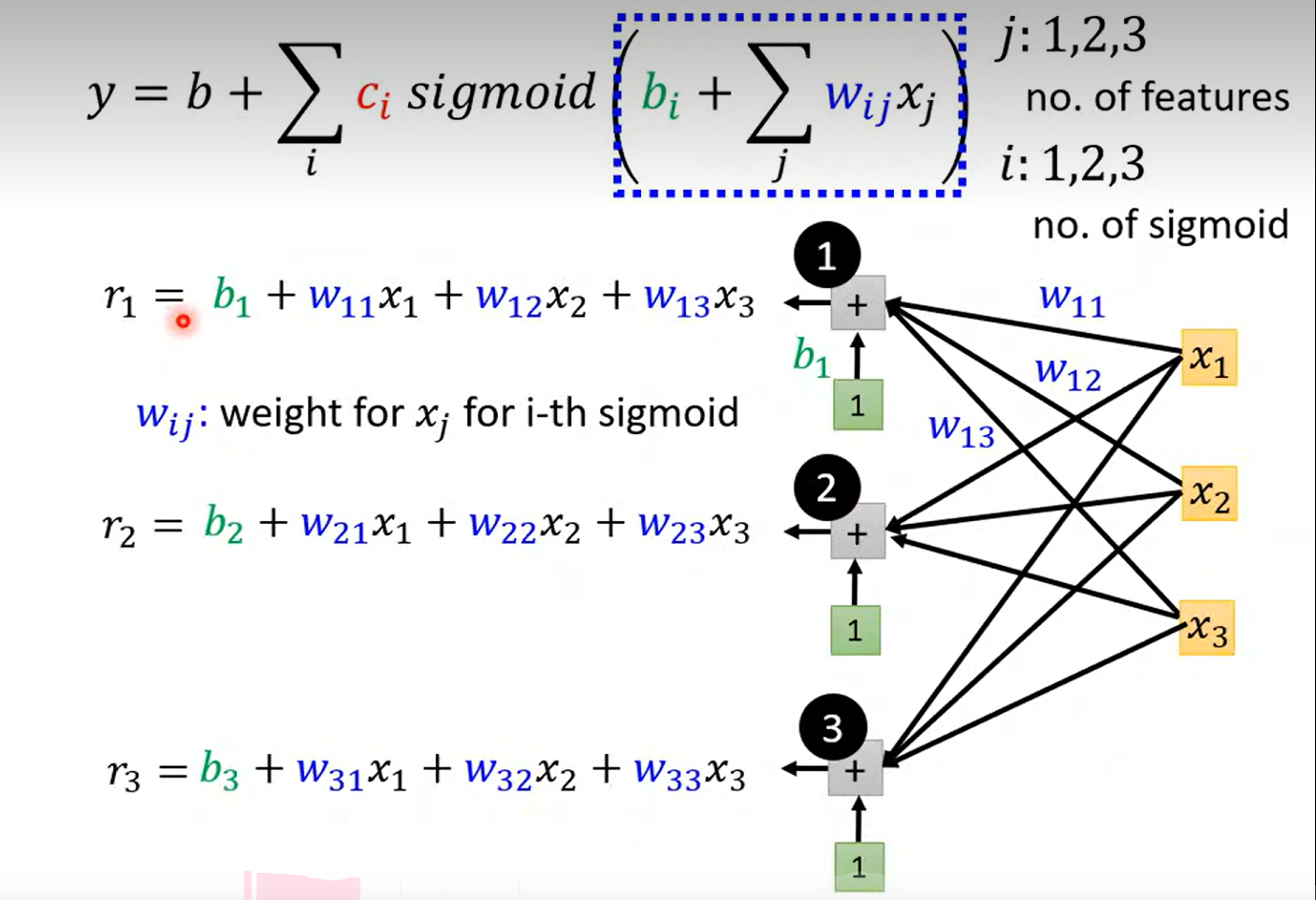
卡住了;
简单顺一下这个图是什么意思: x 表示前 1 2 3 天 的订阅量;
当 j 不变的时候, j = 1 ,表示,通过三个 blue line
去拟合 前一天的订阅量和y(第二天的订阅量)的关系;需要 3*3 +1 = 10 个参数; j = 2 / 3 的时候同上, ok pass ~
注意:w i j _{ij} ij 在这里表示每一个blue line 的斜率,w i j _{ij} ij表示每一个特征在每一次sigmoid 函数中所占的权重
more thinking :
这里的r1 ~r3 表示什么呢?根据式子来理解, 就只能是三种sigmoid 函数方法占预测结果的权重了
Day3
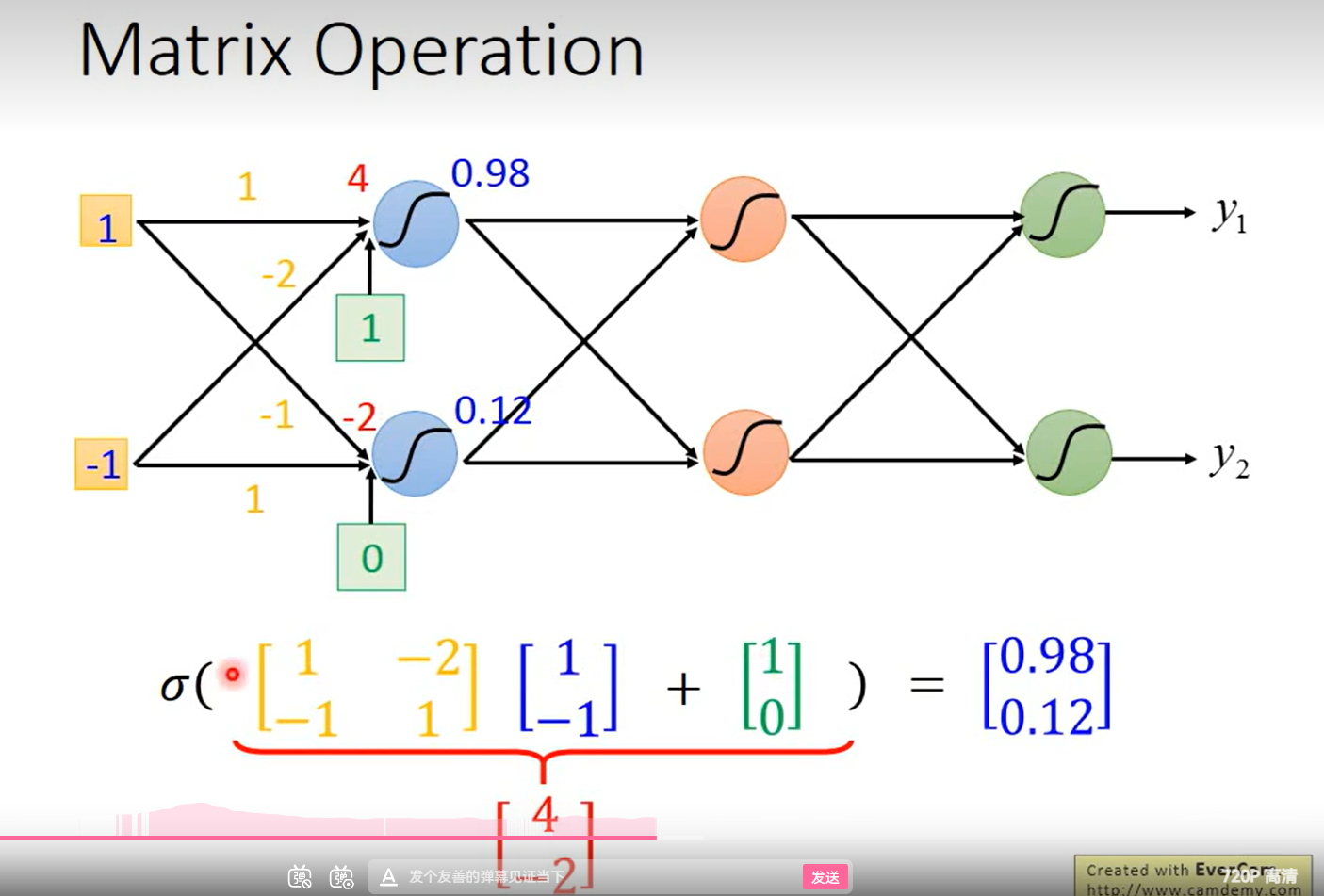
改写为向量和矩阵乘法的格式
接下来就分别把r 放到sigmoid方式里
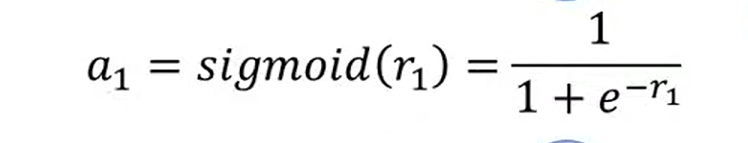
简写以后 (向量化)
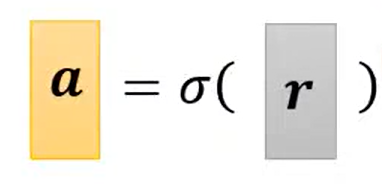
整个过程的向量表示: y = b + cT a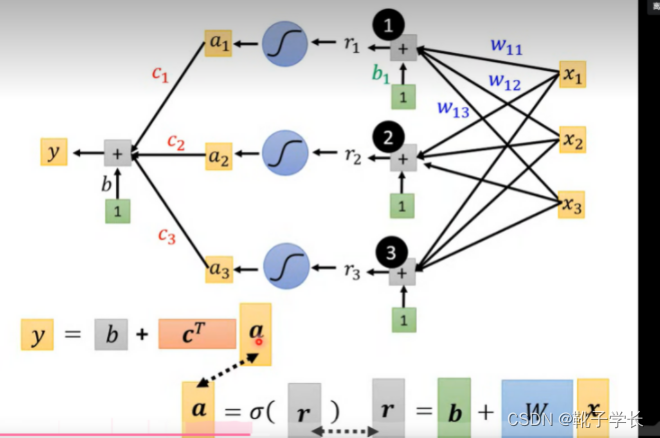
一系列线性代数的表示方法(简洁)
Before we find the parameter (unknown) ,define some variable
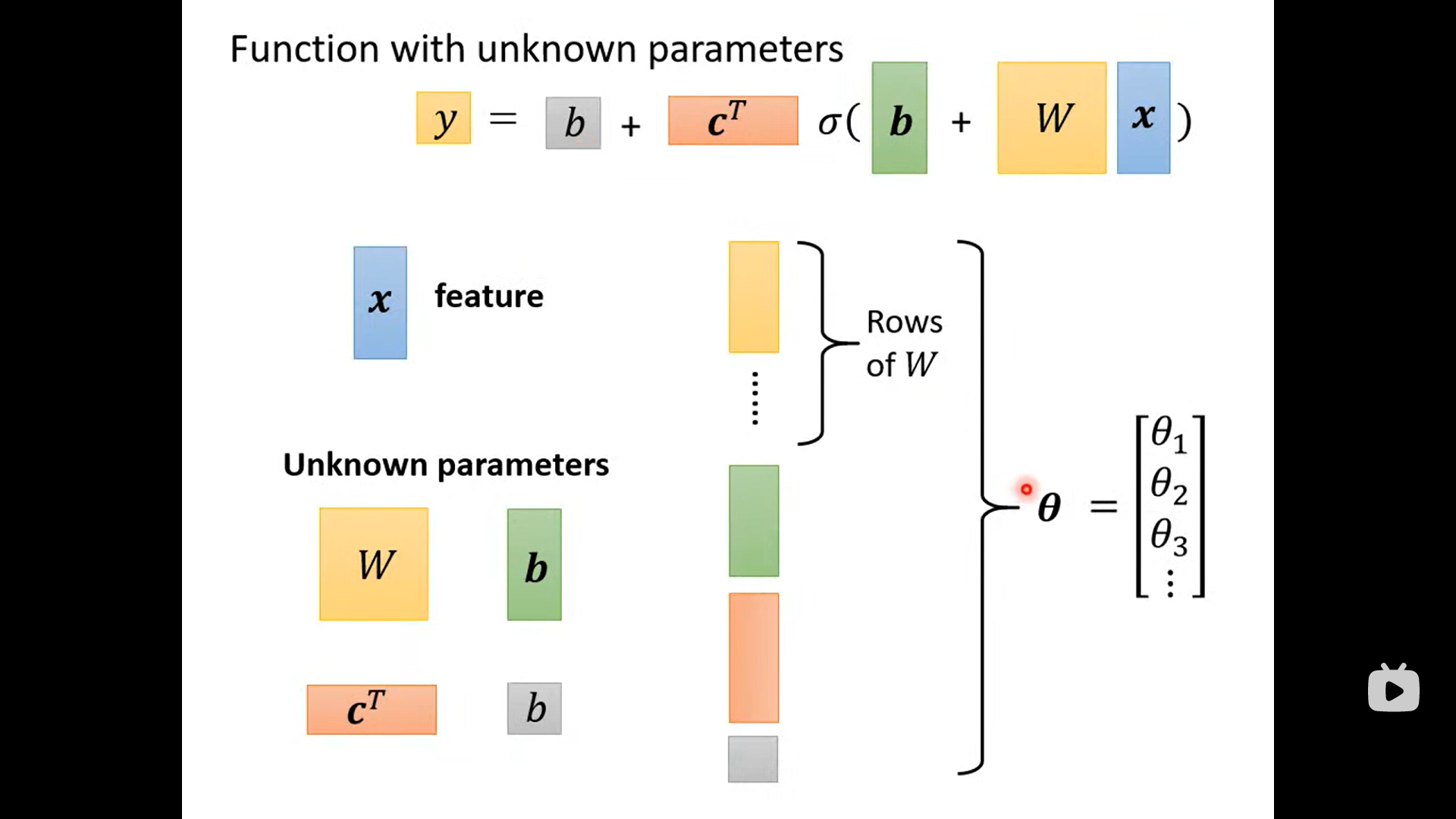
Loss L(theta)

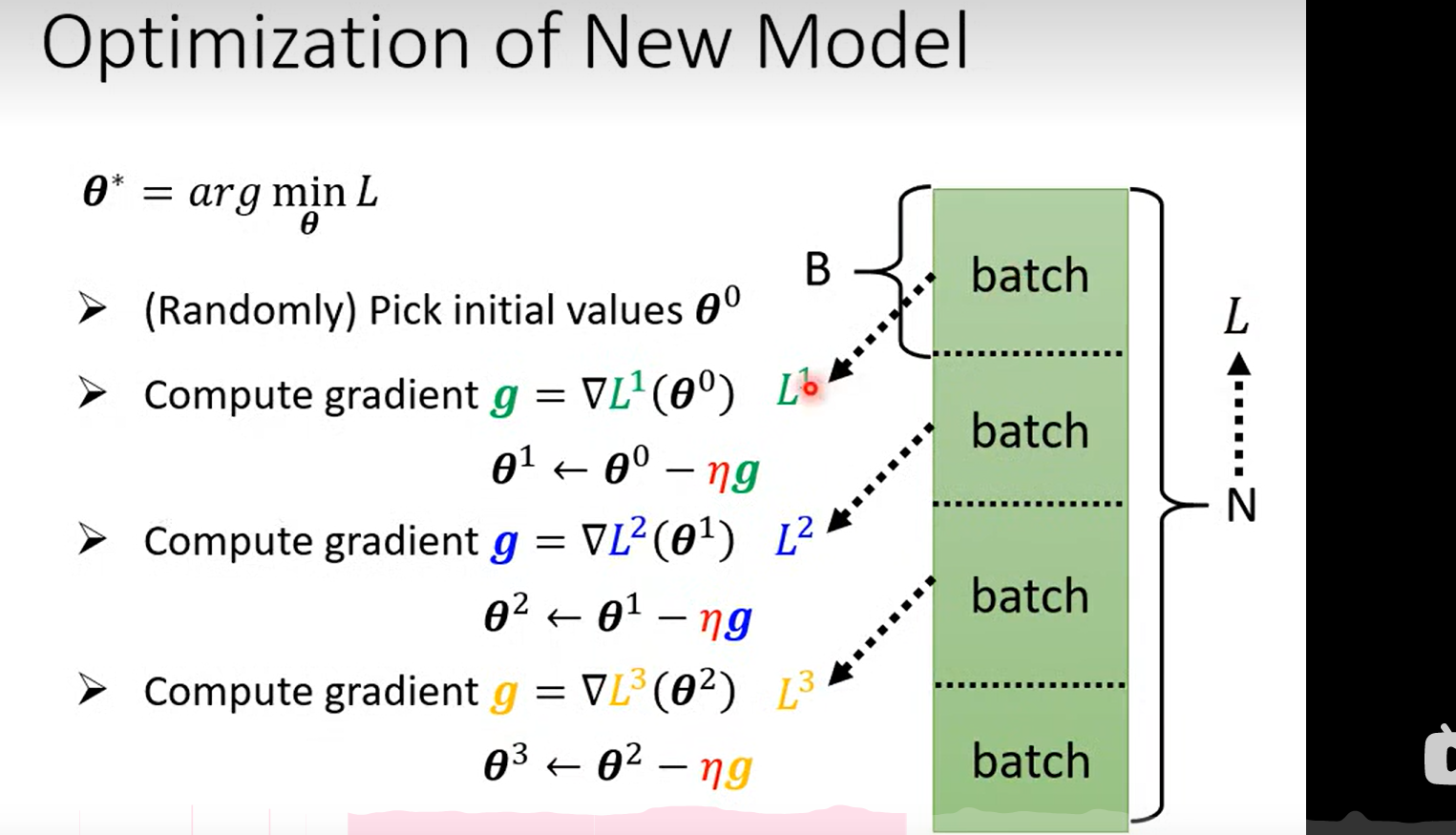
并不是用L 中的数据来训练参数,每一次更新参数的步骤叫做一次 epoch
Q:老师伏笔, 为什么这里要使用batch?
Day4
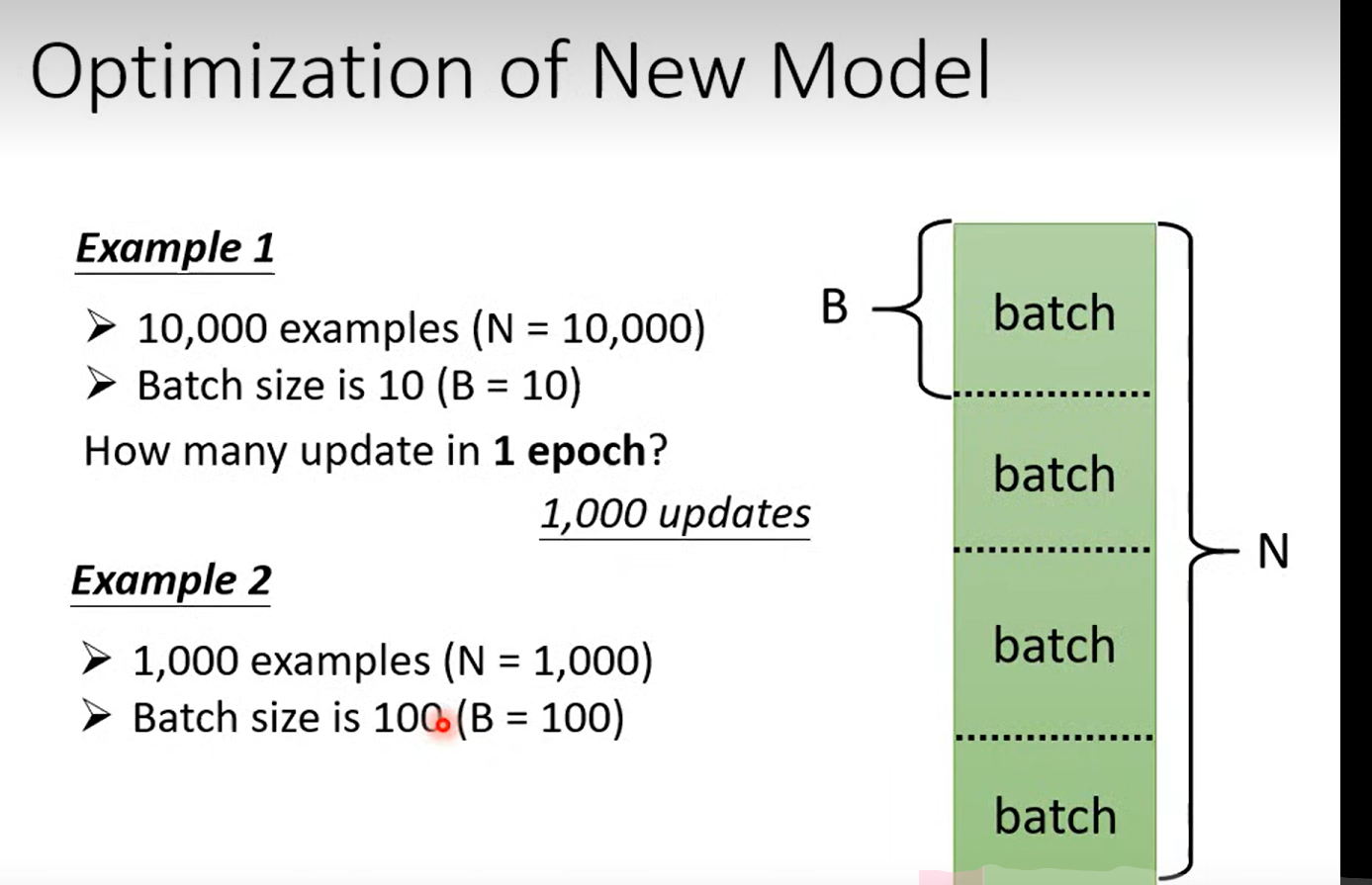
这里的batch Size 也变成了hyperparameter
一个hard Sigmoid 也等于两个relu的叠加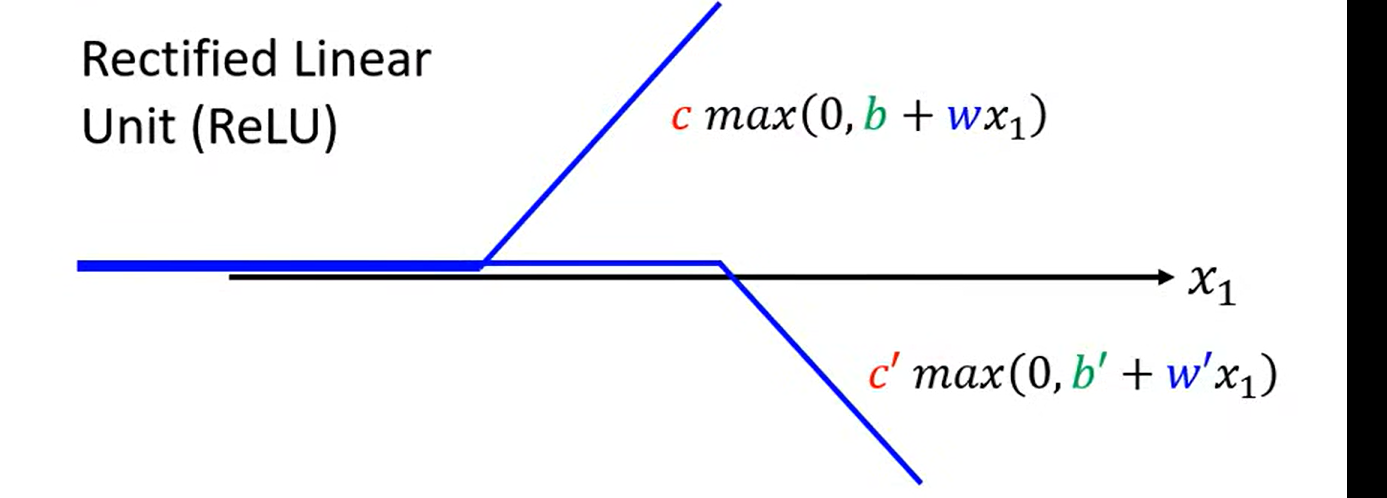
ActivationFunction
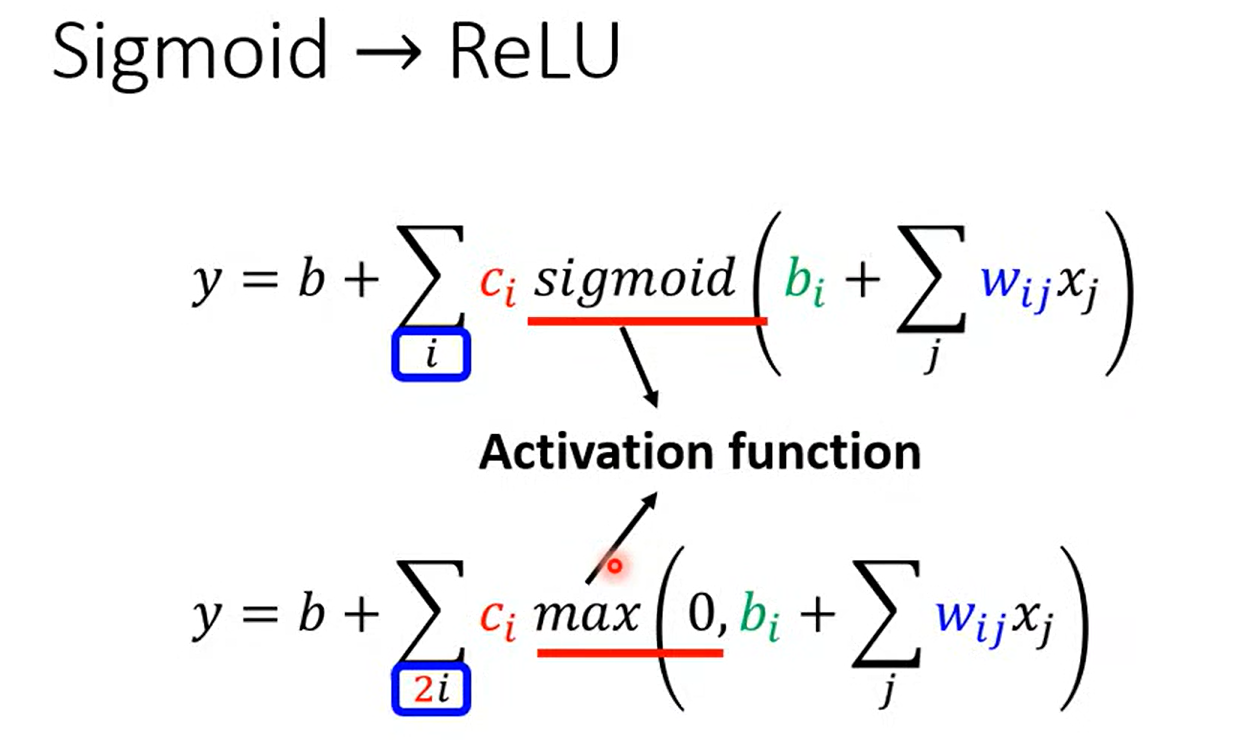
哪一种比较好?
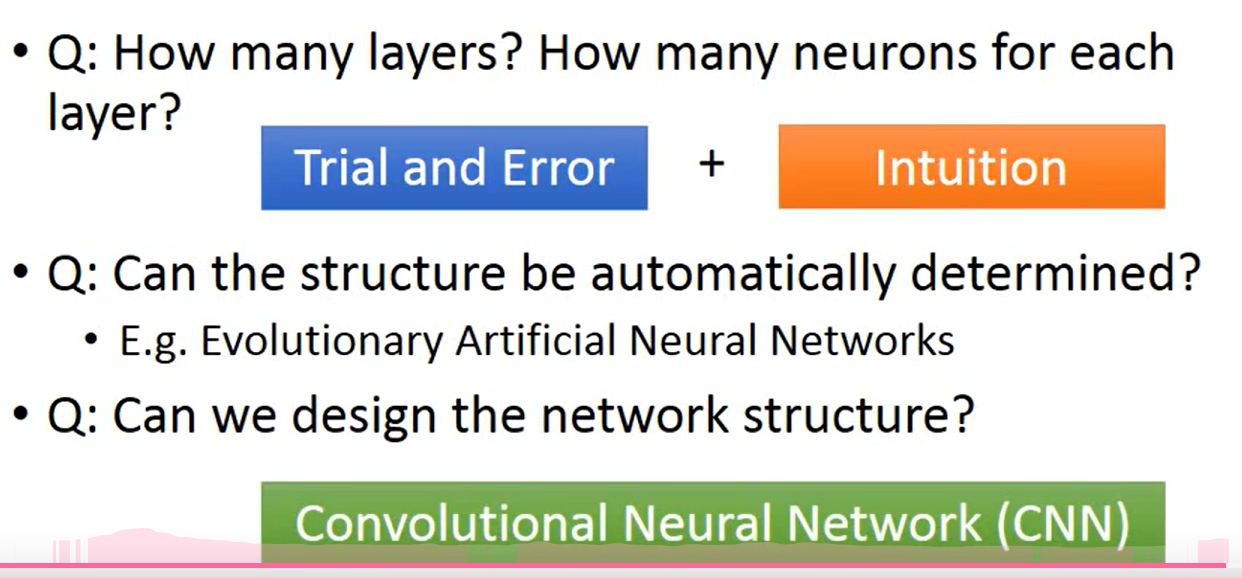
神经网络训练的层数-- 又一个 hyperparameter
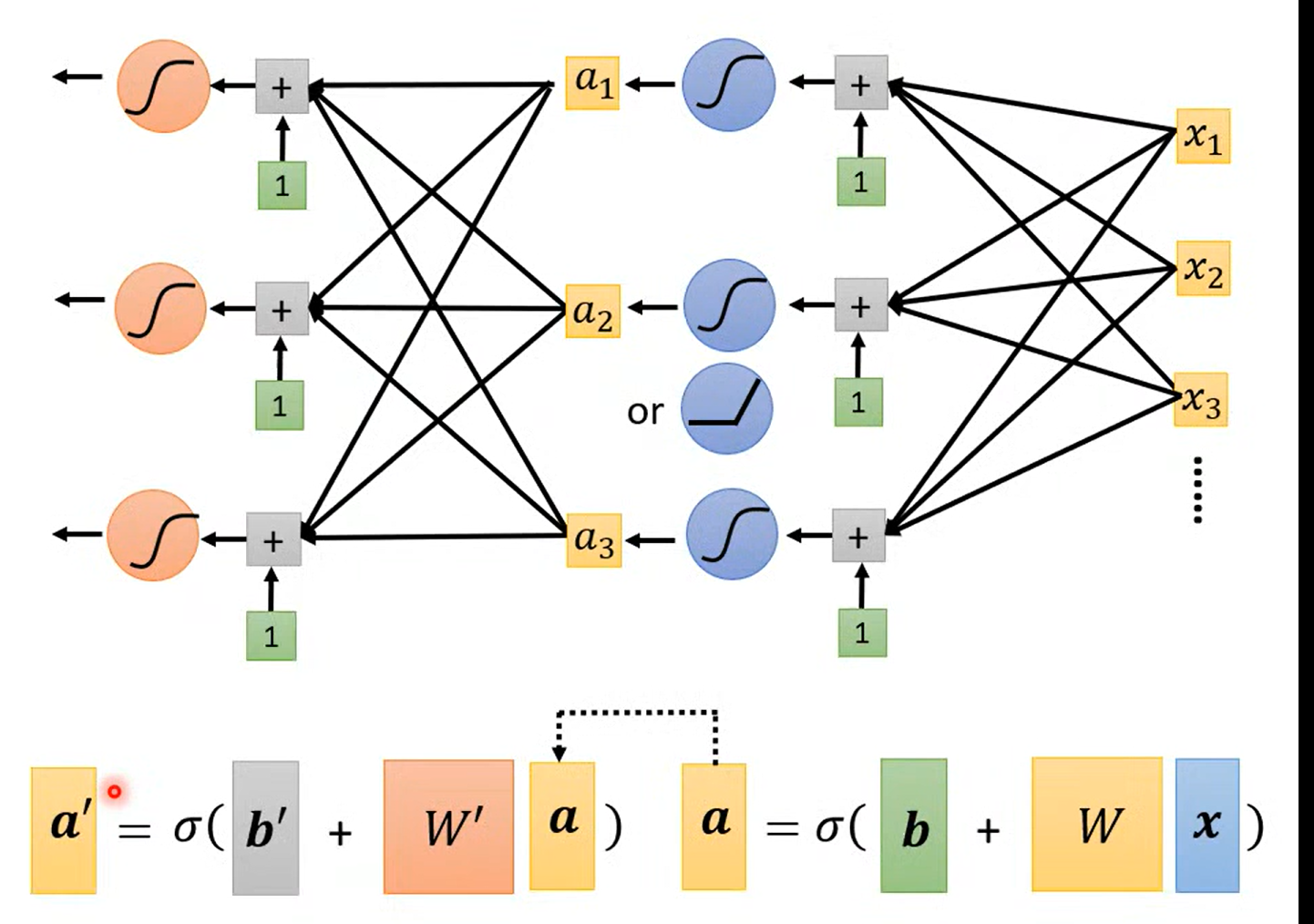
a fancy name
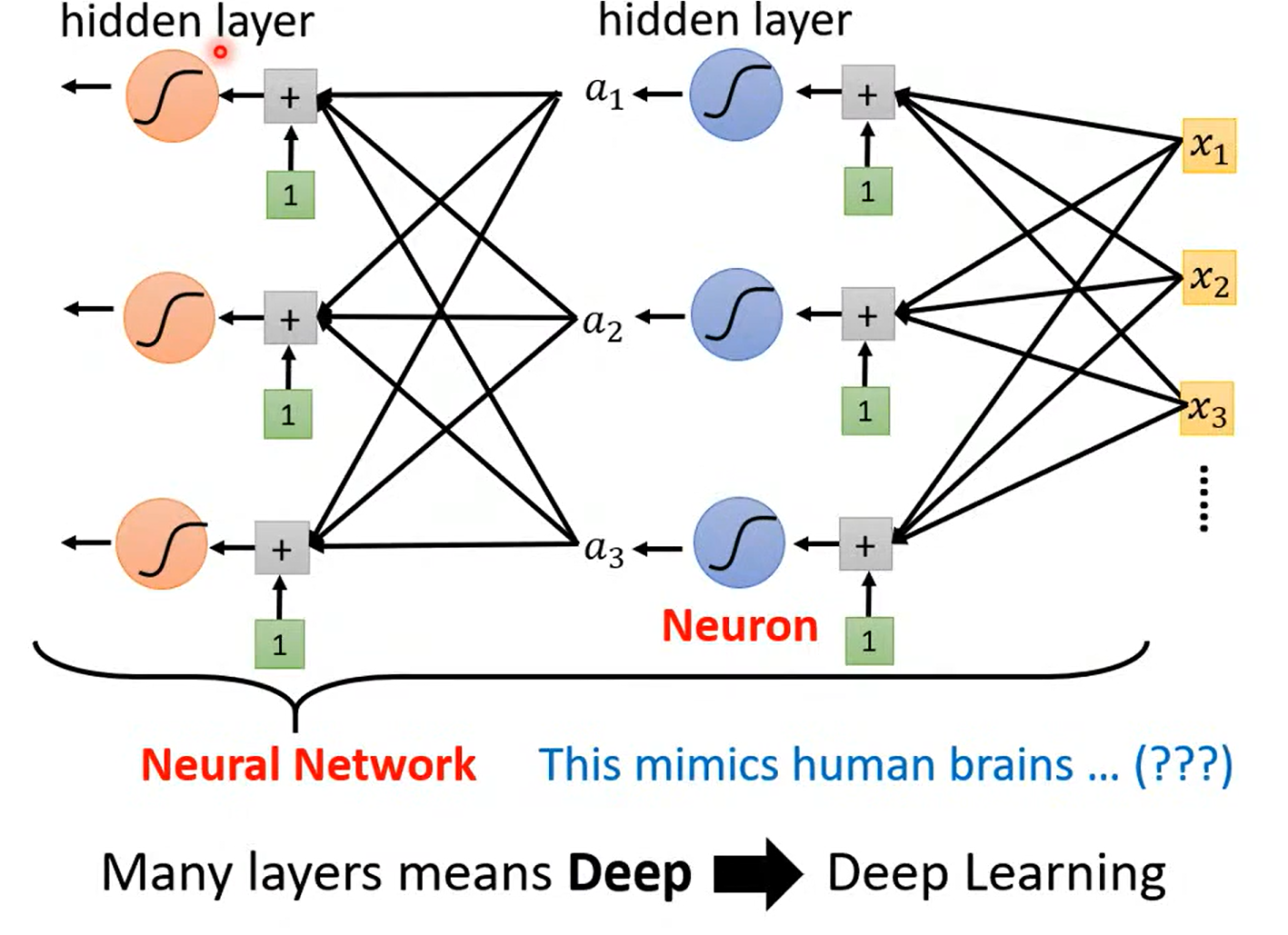
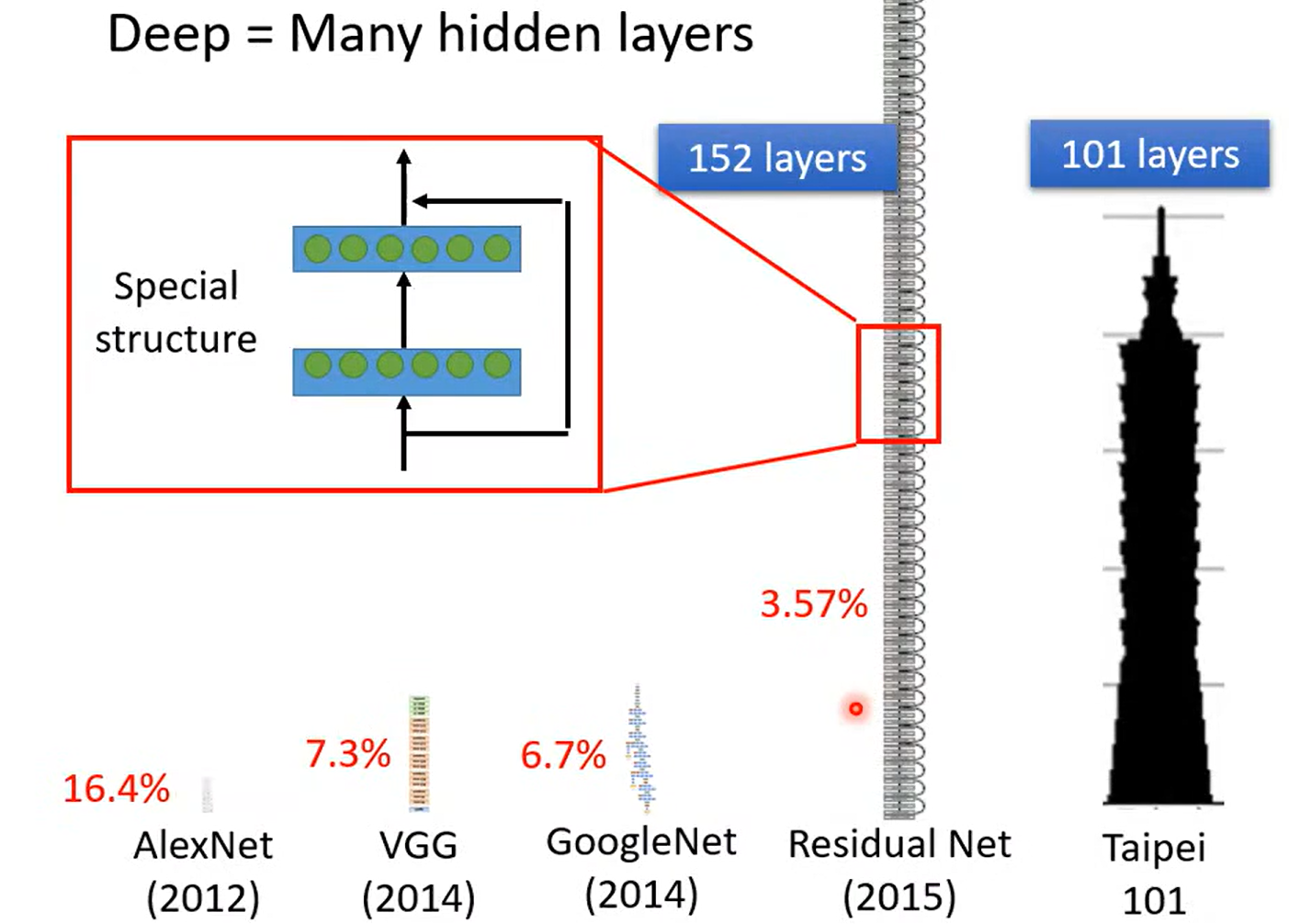
为什么深? 而不更宽呢
Fully connect feedforward
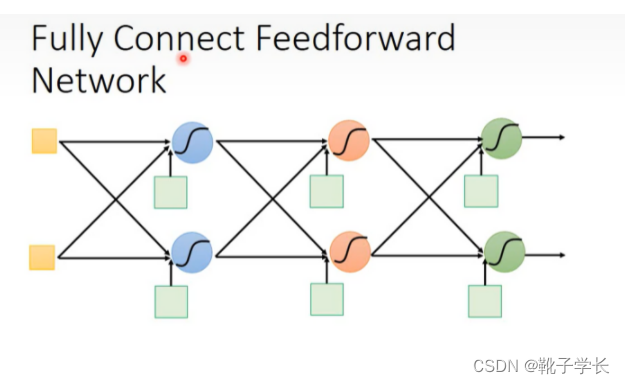
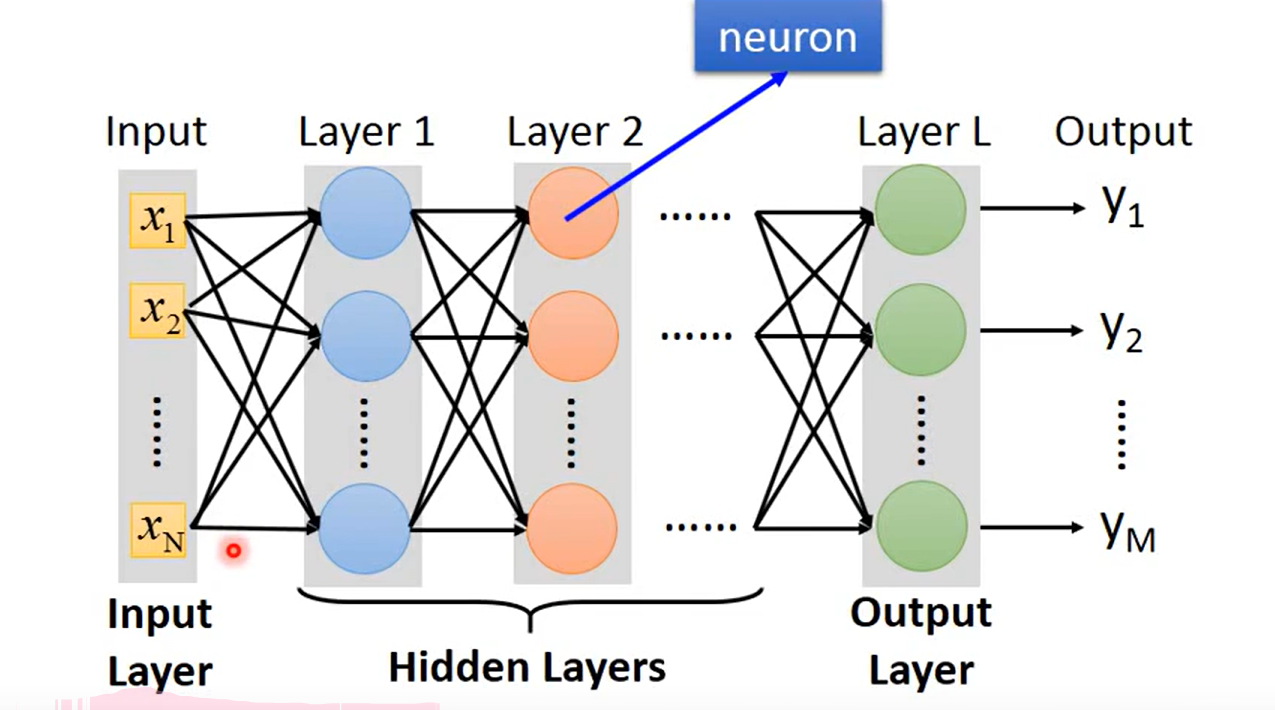
这里可以用来推导矩阵的表示
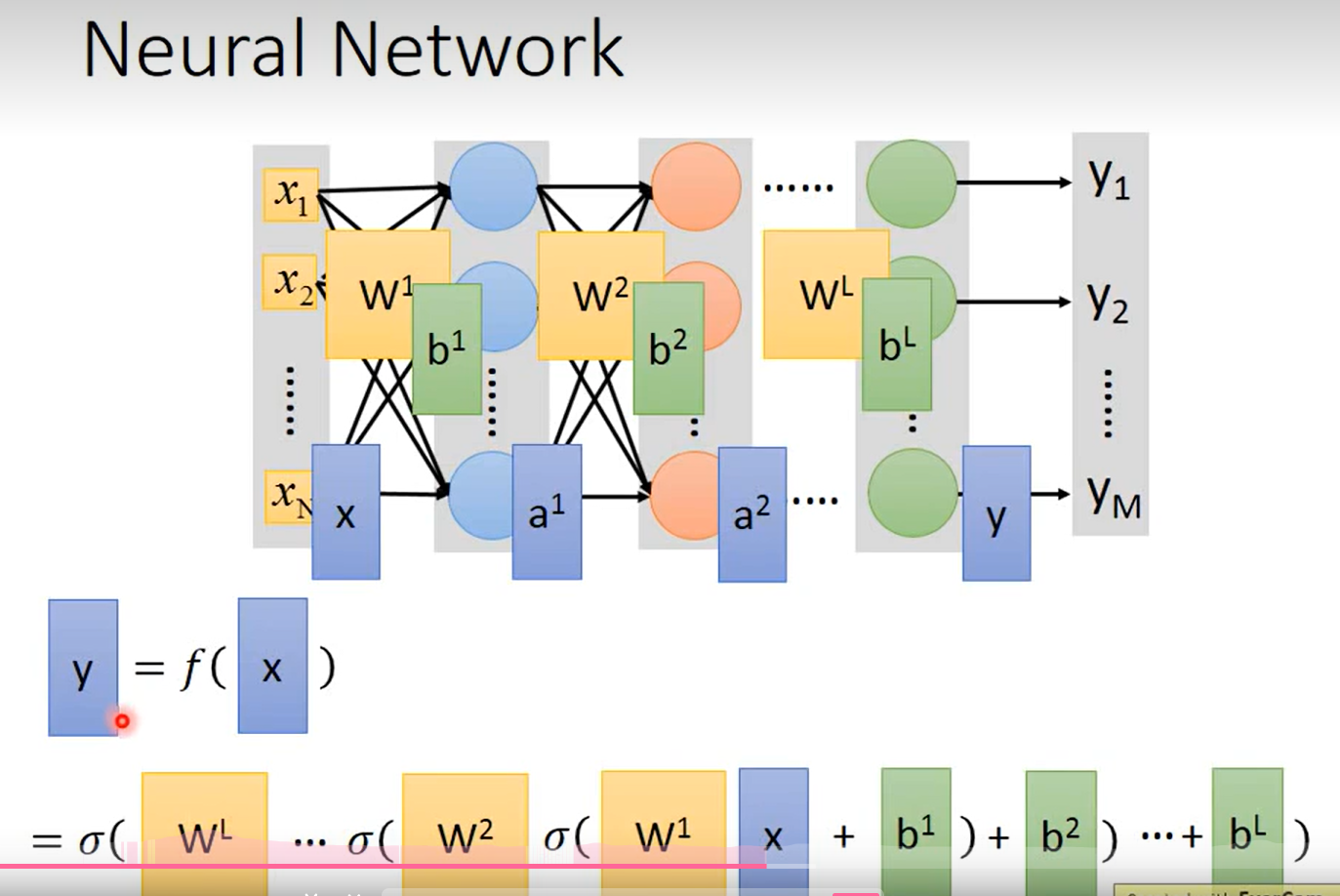
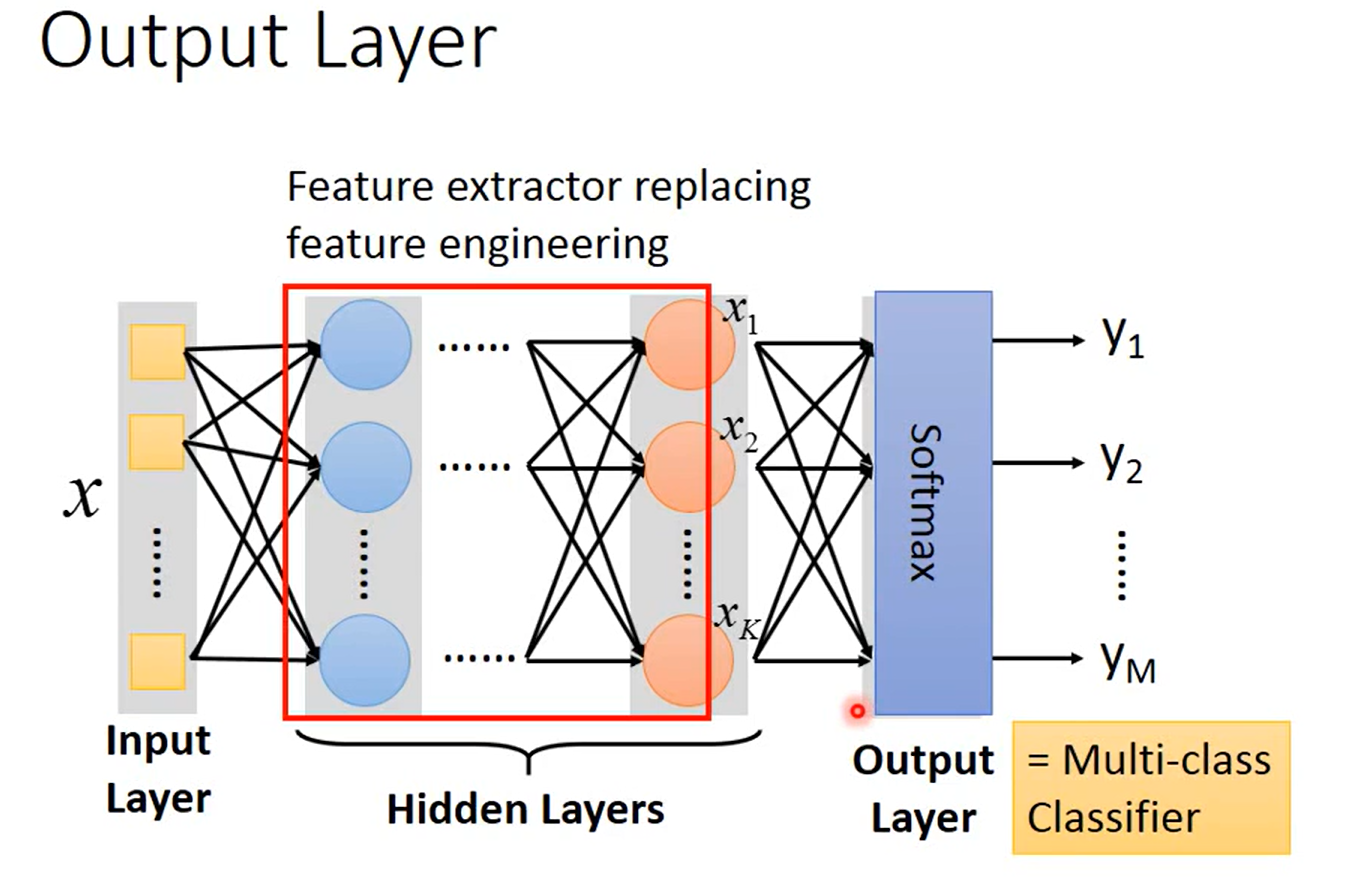
相当于在隐藏层中,做了特征提取;输出层相当于一个多分类器
FAQ
Loss 的定义
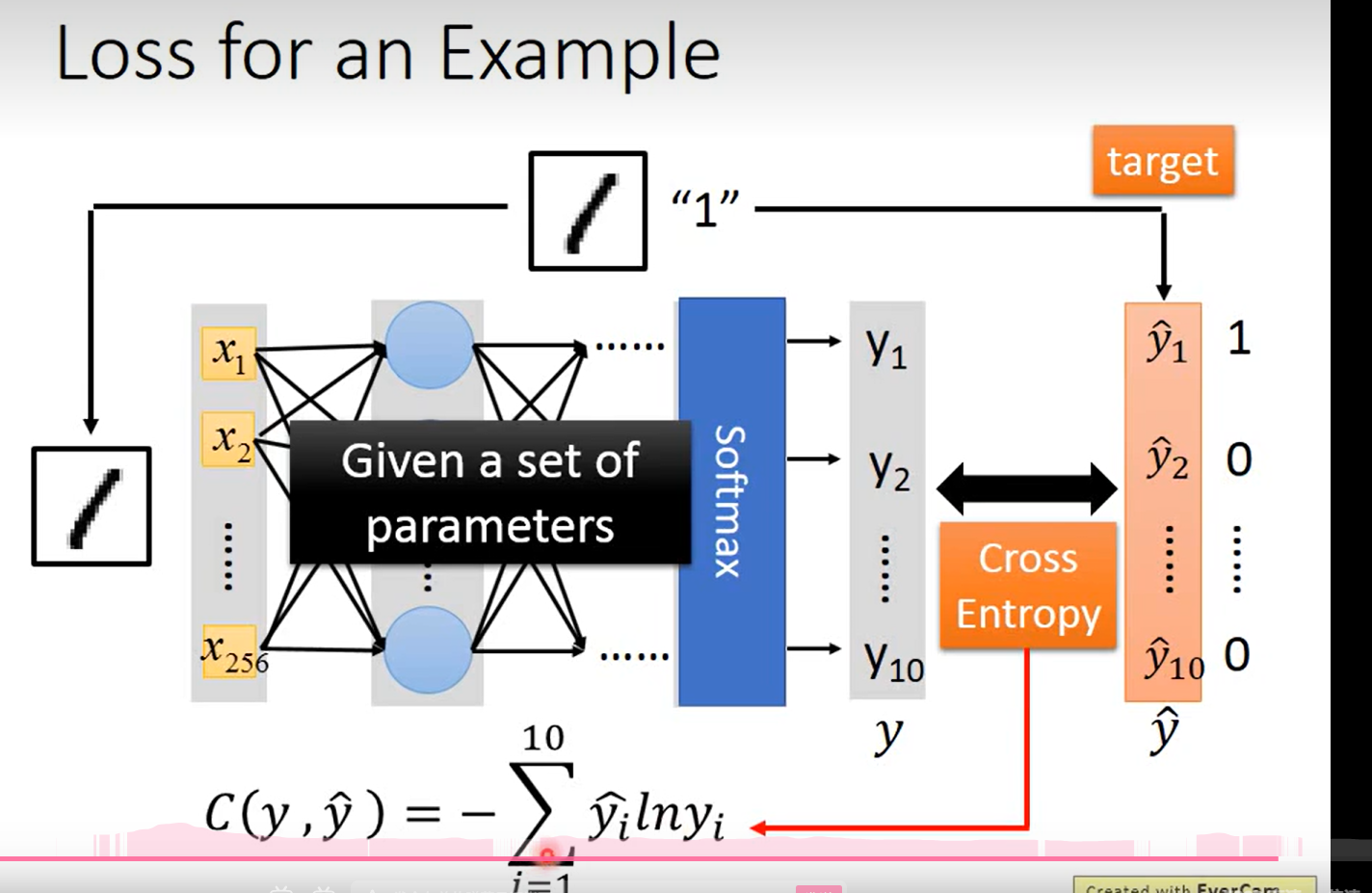
这里的这个函数用的很奇怪,没见过,但是简单分析一下, 这个式子表示的还是y 和 y ’ 的差距;but含奇怪的一点是 这里老师说 让这个参数越小越好 ……不应该是越大越好吗?因为有一个 负号
明白了 应该就是越小越好, 这里老师拿一个多分类的问题举例,所以这里用到了交叉熵的概念, 信息熵越小, 说明信息的混乱程度越小, 分类的 y1 --y10 越精确,之后的loss 见下一页ppt
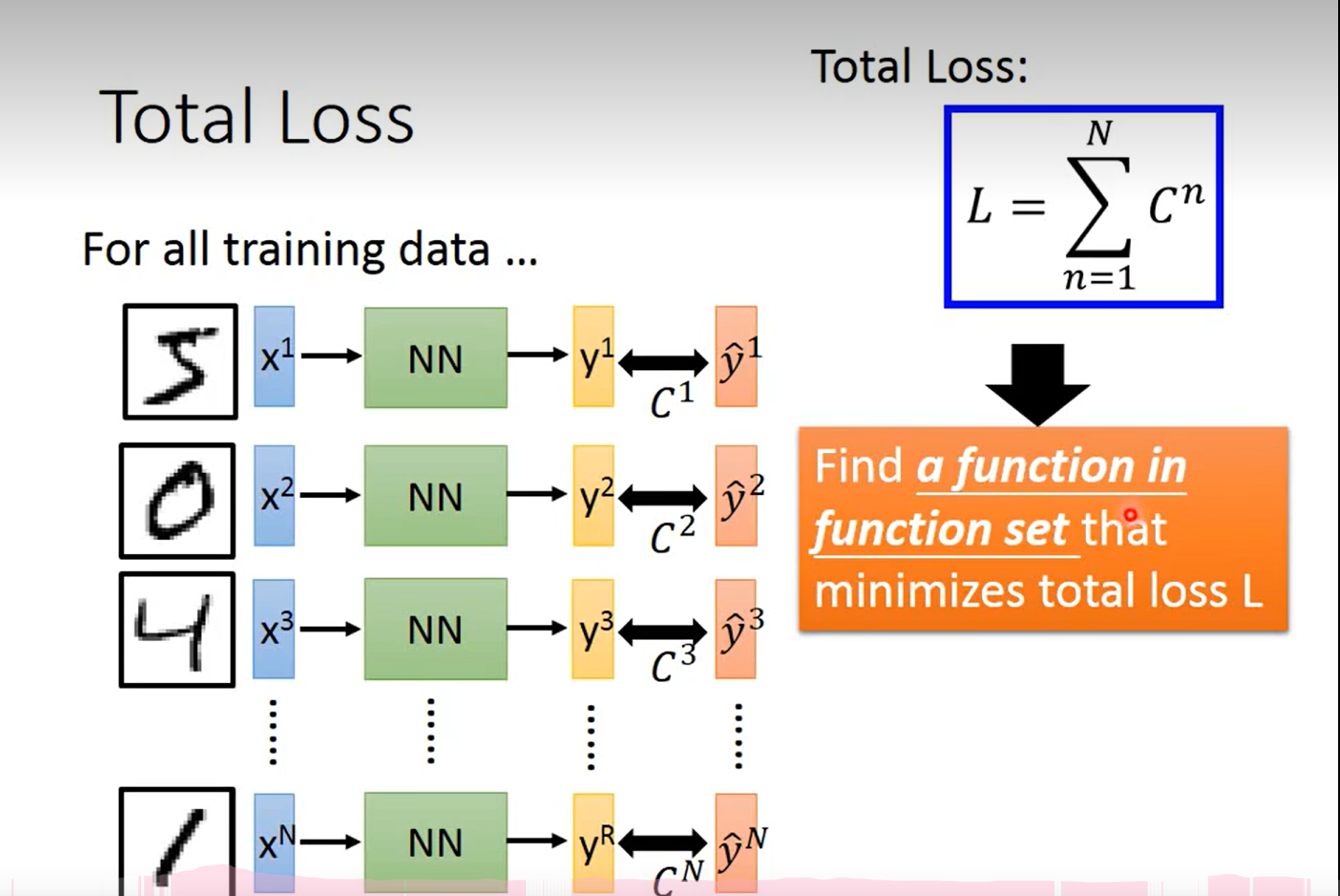
啊 这里Loss 为啥上面的系数是 n 啊…… 哦对,我sb,n表示的是c 的序号,而不是幂次;
怎么回事, 怎么乱糟糟的, 这个c i 到底是什么时候出现的?本质上还是对交叉熵的概念不了解导致的
交叉熵(cross Entropy)
…… 这个概念暂时悬而未解吧
这里注意一下哈,
首先这个交叉熵的概念先放下, 就先用最常见的欧氏距离来表示这里的 y 和y '的差距,ok,第一个问题解决了;
第二点, 为什么这里需要用c i 以及它表示的是什么意思, 简单理解的话就是说, 每一个输入对应的一个输出和真实值的距离;因此有多少组输入就会有多少个c
第三点, c 对w的偏微分 一定是 ci 到 cn 同时进行 且等于 0 的,否则不能保证他们的和最小 (c i 到cn的和)
Day5 BackPropagation
什么是方向传播?
在train neru network 的时候 GradientDiscent的运作方式
Gradient Descent

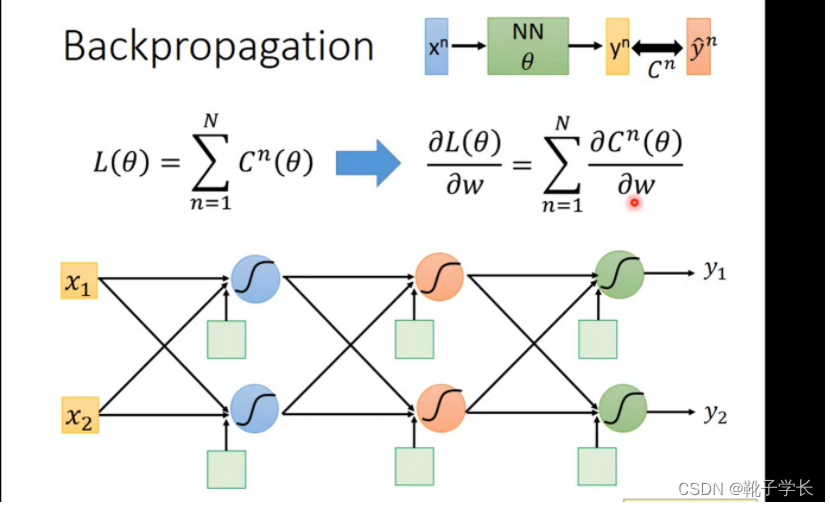
cn 表示 yn 和yn(head) 距离的function
chain Rule
正向传播:
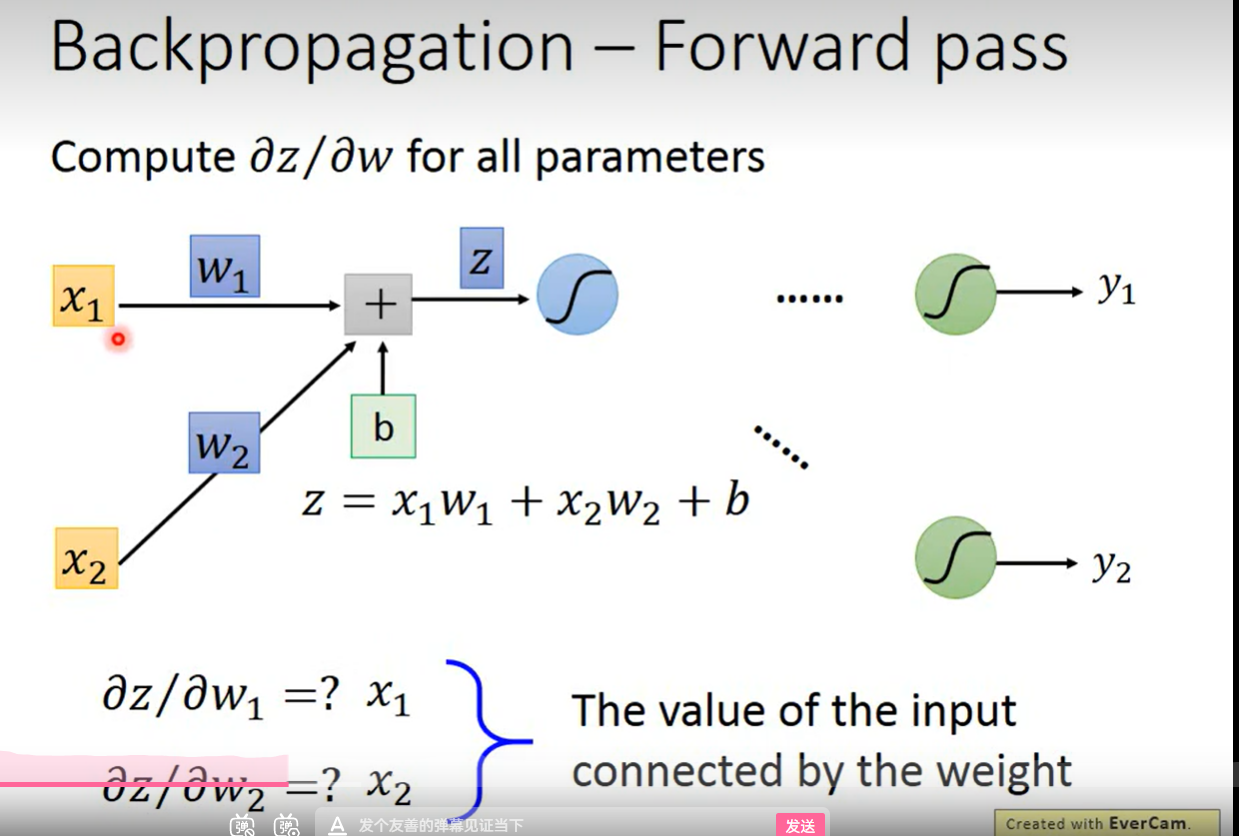
找到规律,对谁的偏微分 ,就等于该输入
反向传播:
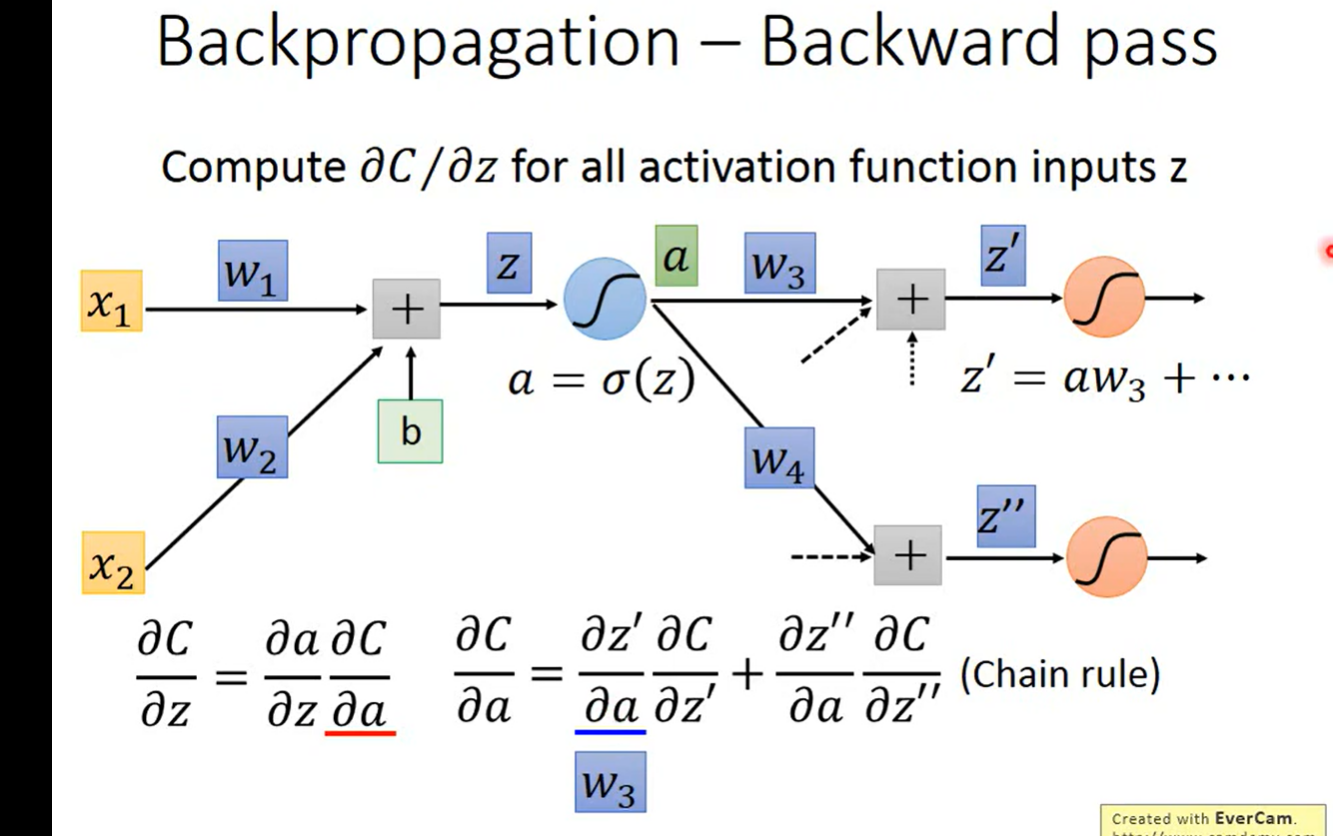
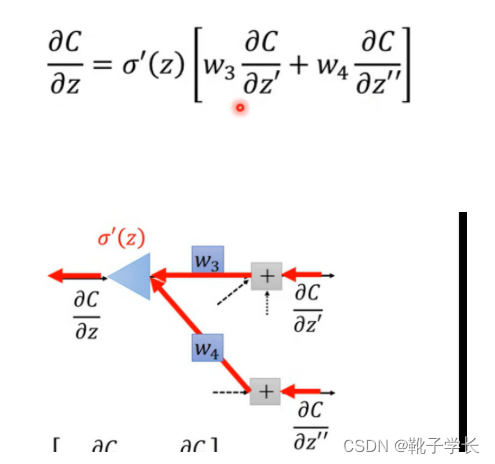
老师这里说 sigmoid ‘(z )是一个常数, 因为z在决定 前馈的 时候就已经决定好了;提问, 为什么?如何理解这个已经决定好了?
如果是按照常数的理解方法的话, z’ 又从何谈起呢?
…… 这个暂时学不进去了
Day6 BackPropagation(2)
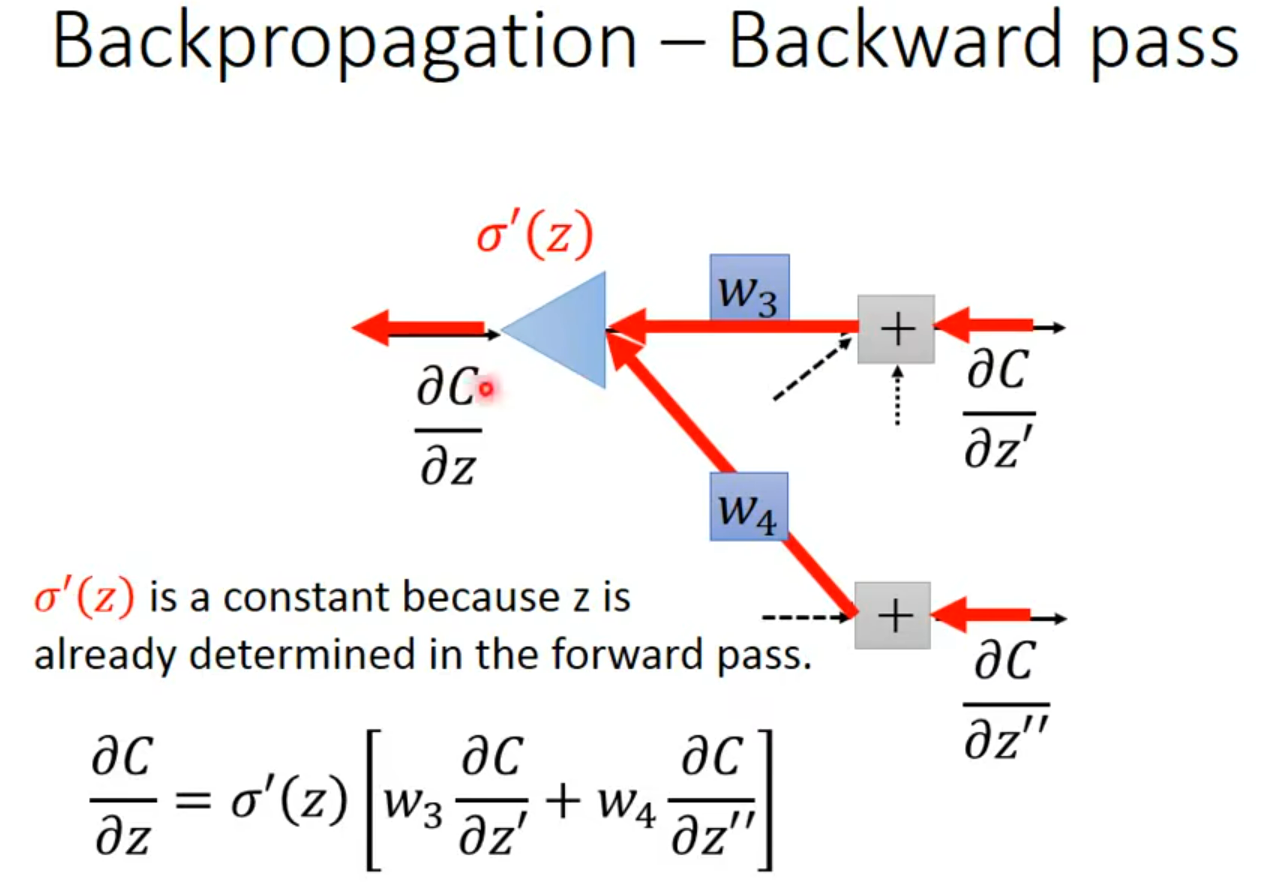
用手推导了一遍具体数字的题目,对反向传播有了更深的理解: 本质上就是梯度下降法;没有丝毫新奇之处;只在于 在深度学习中, L(g(h(……w))),然后我们无法直接求出 L对w 的微分, 需要经过chain rule来进行,这个过程就是反向传播;
至于老师这里说的 sigmoid ‘(z )是一个常数;是因为 z 在前面的前馈中已经计算出来了,就等于输入值和w的线性相加,所以带入以后是一个常数;其实老师讲的很清楚了,是自己对过程不太清晰,把自己绕进去了。
两个case:
case1 . output layer
直接求即可
case2 . hiden layer(not output Layer)
我猜测还是和之前的一样,直到变成case1 为止
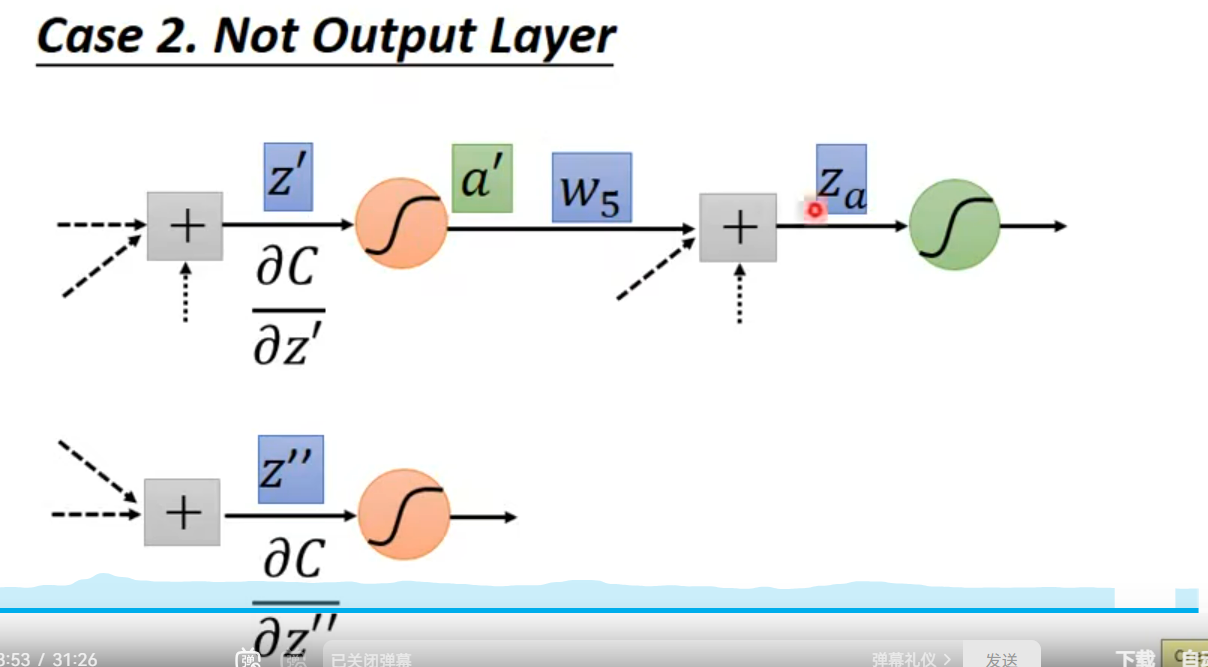
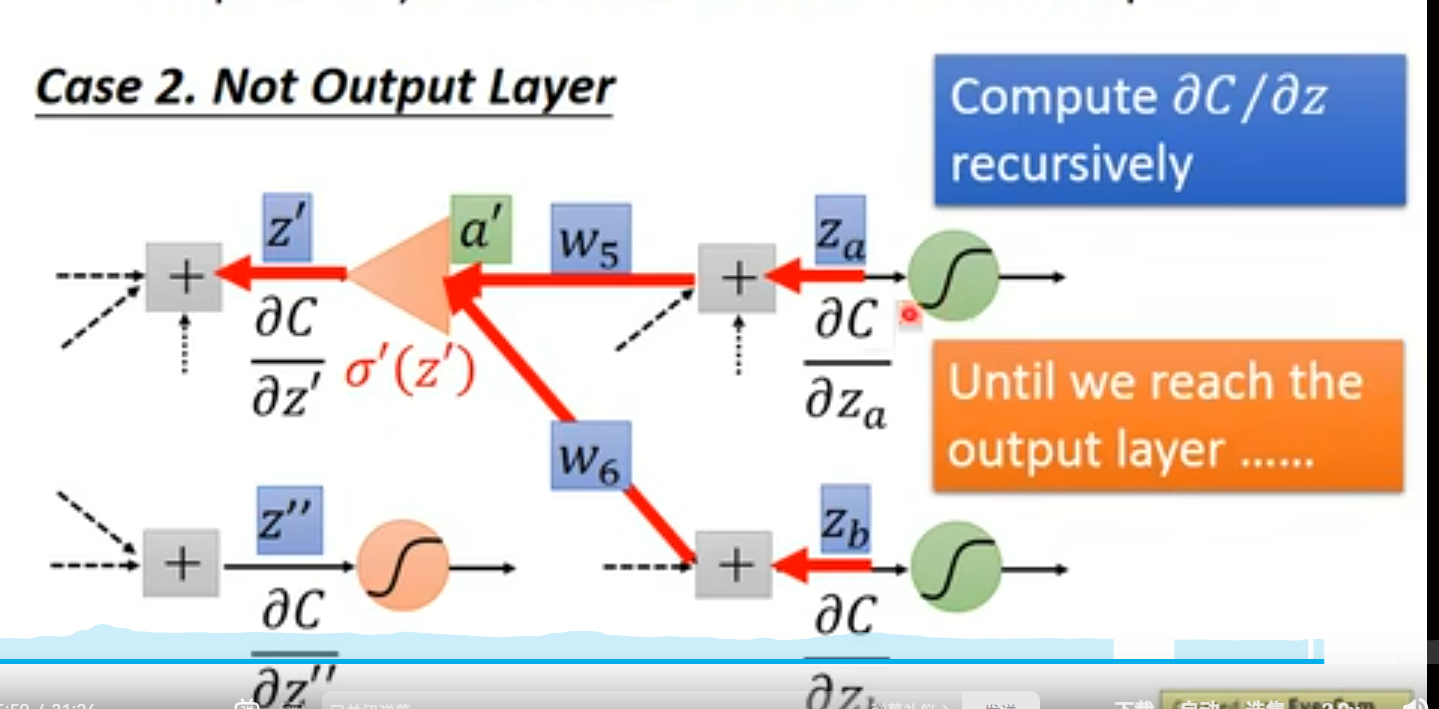
ok 我猜对了~嘿嘿
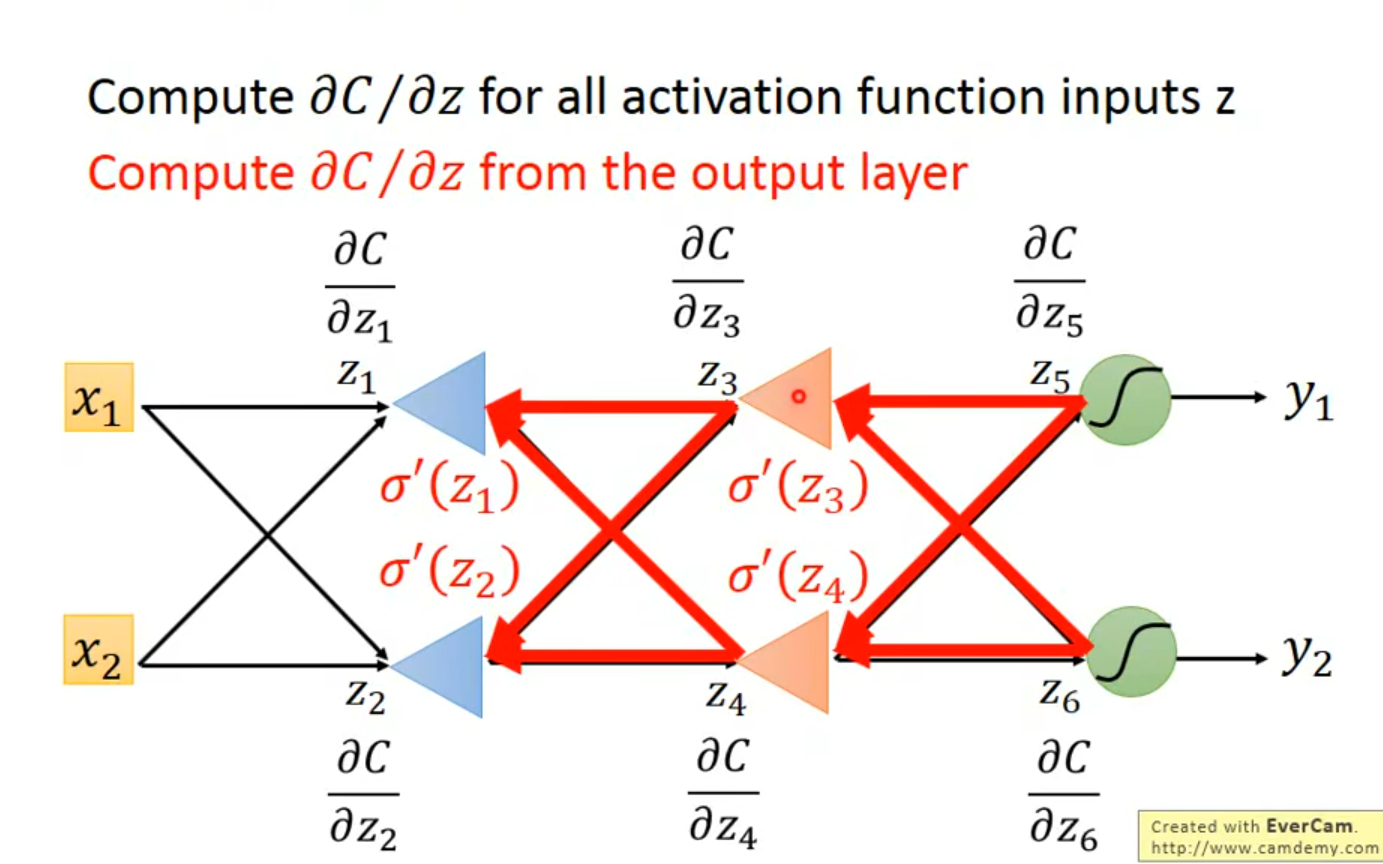
ok 小结一下,反向传播的意义在于减少运算~ 与其正向的求不出来算好几遍 对输出层的偏微分, 不如最开始就直接算 输出层的偏微分
但是扩大的倍率(图中的三角形)需要前一次的正向传播才能求出