本专栏内容为:算法学习专栏,分为优选算法专栏,贪心算法专栏,动态规划专栏以及递归,搜索与回溯算法专栏四部分。 通过本专栏的深入学习,你可以了解并掌握算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:算法从入门到精通
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
专题四
- 前缀和
- 算法原理:
- 解法一:
- 解法二:
- 二维前缀和
- 算法原理:
前缀和

算法原理:
我们先分析一下题目:
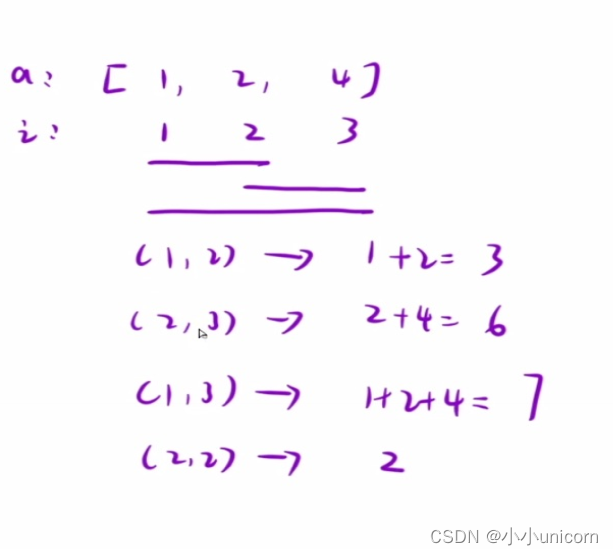
题目的意思是求给定区间的和,区间由用户决定。
解法一:
看到这个题目,我们首先想到的是暴力+枚举来解决这个情况。

把所有询问q次的子数组都枚举出来,但是题目给的数据很大,肯定会超时。因为每q次询问都要把整个数组遍历一遍,因此时间复杂度为 n ∗ q n*q n∗q
在此基础上我们可以进行优化:
解法二:
解法二就是我们要介绍的前缀和知识。
前缀和是什么?首先我们要知道一点:前缀和可以快速求出数组中某一个连续区间的和。其次前缀和可以降低时间复杂度,对于本题而言,暴力+枚举时间复杂度达到了 n ∗ q n*q n∗q而利用前缀和进行优化就可降低到 q q q;
前缀和分两步:
- 预处理一个前缀和数组:
- 使用前缀和数组
第一步:
什么是一个前缀和数组?我们要先明确一点,其实前缀和就是一个简单的动态规划。我们首先创一个dp数组(下标数组)。这个数组i位置的值代表从[1,i]区间内所有元素的和。也就是说:
dp[i]表示从[1,i]区间内所有元素的和
接下来我们分析一下递推:
注意数组的下标是从1开始而不是从0开始。
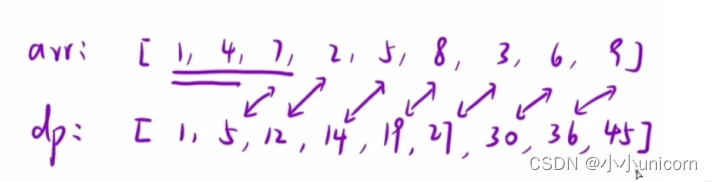
arr数组为原数组,dp[2]的值代表原数组区间[1,2]内元素的和,也就是5,dp[3]的值为原数组前三个数相加的结果,那么dp[4]就是原数组前4个数相加的结果,但是从dp数组的第三个位置开始,我们也可以是dp[2]+上原始第三个位置的值,也就是 d p [ 3 ] = d p [ 2 ] + a r r [ 3 ] dp[3]=dp[2]+arr[3] dp[3]=dp[2]+arr[3];依次内推最后一个元素的位置就是 d p [ i ] = d p [ i − 1 ] + a r r [ i ] dp[i]=dp[i-1]+arr[i] dp[i]=dp[i−1]+arr[i];
而 d p [ i ] = d p [ i − 1 ] + a r r [ i ] dp[i]=dp[i-1]+arr[i] dp[i]=dp[i−1]+arr[i]就是我们要找的递推关系式子,而其实这个式子也可以称为动态规划里面的状态转移方程。
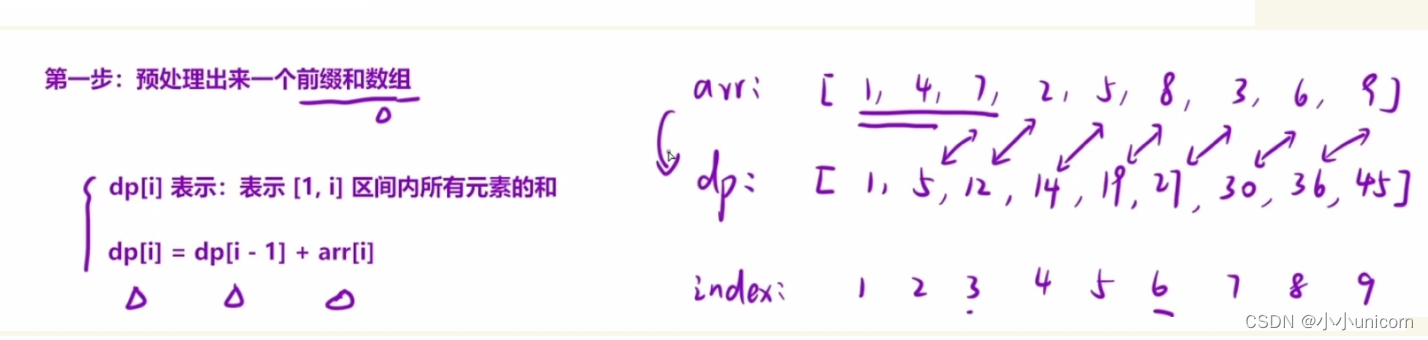
预处理做好后,接下来就是第二步:
我们应该如何使用前缀和数组呢?
我们先分析一下:
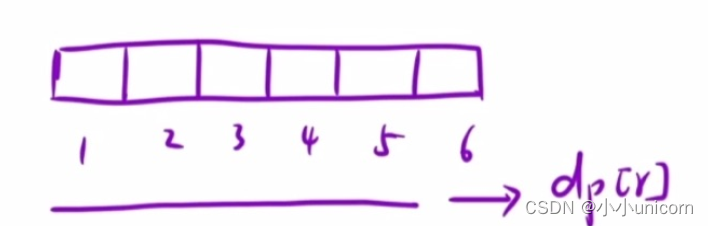
现在我们的dp数组里面存放的值分别是从1位置开始到i位置结束该区间所有元素的和。那么我们如何求里面具体某一段的和呢?
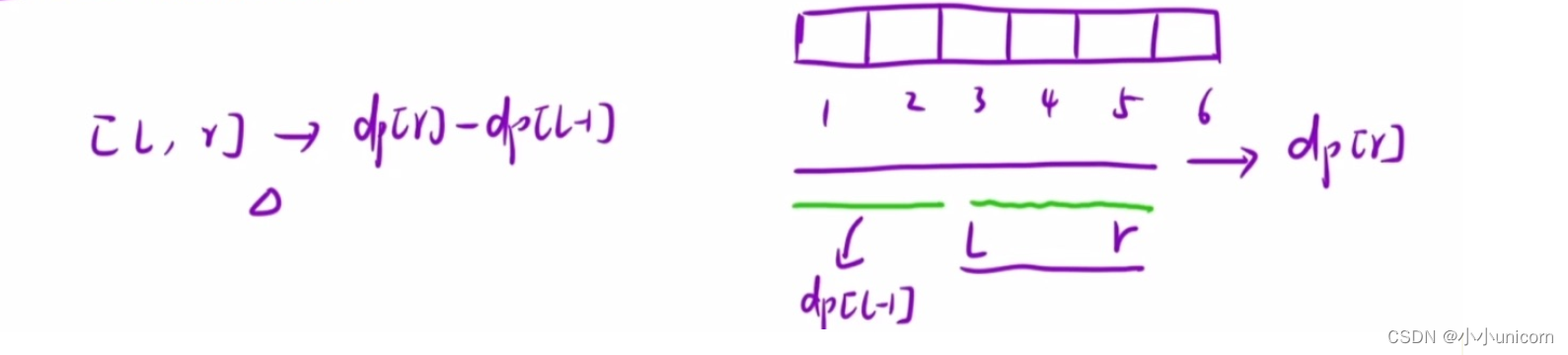
其实很简单,就比如我们要求[3,5]区间的和,我们[1,5]的和是知道的,[1.2]的和是知道的,我们用[1,5]区间的和-去[1,2]的和不就是我们所求的吗?
我们抽象出来,l和r,那么[l,r]区间的和就是 d p [ r ] − d p [ l − 1 ] dp[r]-dp[l-1] dp[r]−dp[l−1]
介绍到这,我们一维前缀和知识基本上差不多了,但是还有个小问题,别忘了我们数组下标是从1开始的,为什么不从0开始呢?这其实就是为了防止边界情况。

假设我们要求的区间是[0,2]那么对用我们的递推式:
dp[2]-dp[-1],就会产生越界,这里就需要我们对边界情况做特殊处理。
代码实现:
#include <iostream>
#include<vector>
using namespace std;int main()
{//1.读入数据int n=0,q=0;cin>>n>>q;vector<long long > arr(n+1);for(int i=1;i<=n;i++){cin>>arr[i];}//2.预处理出来一个前缀和数组vector<long long > dp(n+1);for(int i=1;i<=n;i++){dp[i]=dp[i-1]+arr[i];}//3.使用前缀和数组int l=0,r=0;while(q--){cin>>l>>r;cout<<dp[r]-dp[l-1]<<endl;}return 0;
}
二维前缀和

算法原理:
有了一维前缀和的经验,接下来我们介绍二维前缀和。
首先还是要预处理一个二维前缀和数组出来:
在预处理之前,我们先分析一下:
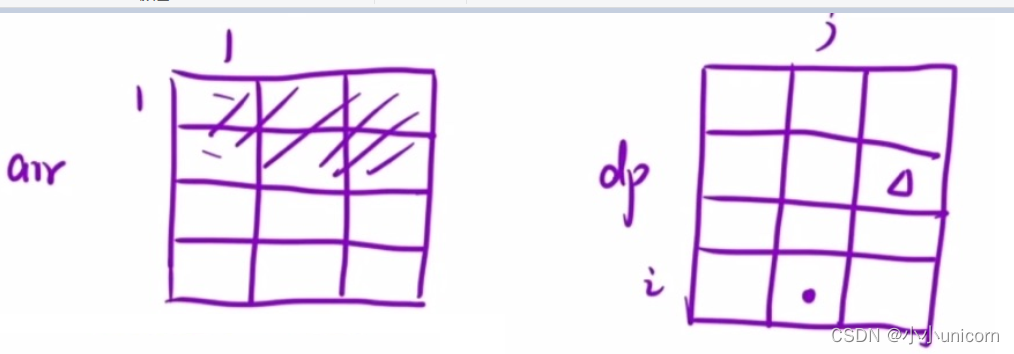
首先肯定要弄一个跟原数组大小一样的二维数组,我们的dp二位数组里面放的是某区间的和。那么我们的
dp[i][j]就表示:从[1,1]位置到[i][j]位置,这段区间内所有元素的和。
一维好说,这二维看着和想求出来不简单啊,既然直接求不来,那么我们就去而求其次。
咱们把整个面积分成四块:A,B,C,D
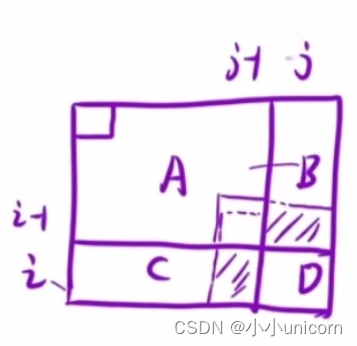
那么我们的 d p [ i ] [ j ] = A + B + C + D dp[i][j]=A+B+C+D dp[i][j]=A+B+C+D;
柿子先挑软的捏,D区域肯定是我们最好求的,D区域对应原数组不就是arr[i];不仅如此,A也可以求,A区域为dp[i-1][j-1];
B和C怎么求呢?
既然不好求那干脆我们不求,我们换个角度看:AB区域和AC区域其实很好求,然后看整体:
我们要求整个面积可以这样求:
( A + B ) + ( A + C ) + D − A (A+B)+(A+C)+D-A (A+B)+(A+C)+D−A

分析到这,我们的递推关系式其实已经出来了:
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] + a r r [ i ] [ j ] − d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1] dp[i][j]=dp[i−1][j]+dp[i][j−1]+arr[i][j]−dp[i−1][j−1]
接下来就是第二步:
如何使用:
其实分析到这,使用二维前缀和数组肯定也是要间接求:
给定区间求[x1,y1]到[x2,y2]区间内的和,也就是求D区域。从左上角绿格子到右下角绿格子的这部分区域的值。D区域可以将整个分为4部分A,B,C,D
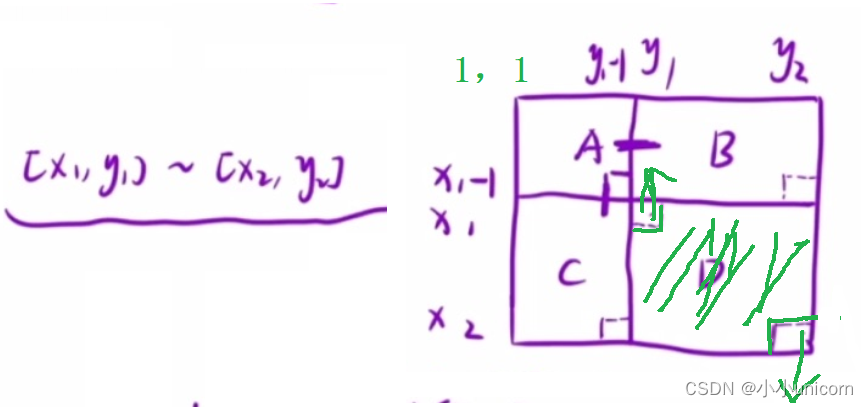
那么我们的D可以这样求:
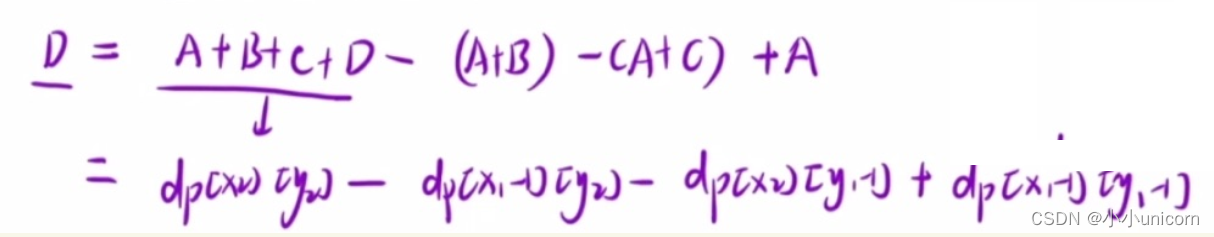
D = A + B + C + D − ( A + B ) − ( A + C ) + A D=A+B+C+D-(A+B)-(A+C)+A D=A+B+C+D−(A+B)−(A+C)+A
那么我们的递推是也就出来了
d p [ x 2 , y 2 ] − d p [ x 1 − 1 ] [ y 2 ] − d p [ x 2 ] [ y 1 − 1 ] + d p [ x 1 − 1 ] [ y 1 − 1 ] dp[x2,y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1] dp[x2,y2]−dp[x1−1][y2]−dp[x2][y1−1]+dp[x1−1][y1−1]
代码实现:
#include<iostream>
#include<vector>
using namespace std;int main()
{//1.输入数据int n=0,m=0,q=0;cin>>n>>m>>q;vector<vector<long long>> arr(n+1,vector<long long>(m+1));for(int i=1;i<=n;i++){for(int j=1;j<=m;j++)cin>>arr[i][j];}//2.预处理前缀和数组vector<vector<long long>> dp(n+1,vector<long long >(m+1));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];//3.使用前缀和数组int x1,y1,x2,y2;while(q--){cin >> x1>> y1>>x2>>y2;cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;}return 0;
}