二分查找-图文详解，看不懂你来打我。。。

一、查找算法

在计算机科学和算法领域，搜索是一项基本的任务。在海量数据中寻找特定的元素是一项常见的任务，而二分查找（Binary Search）是一种非常高效的搜索算法，特别适用于有序数组。

二、二分查找

二分查找是一种常用的查找算法。在有序数组中查找目标元素时，二分查找通过将数组分成两部分，然后判断目标元素在哪一部分中，从而缩小查找范围，提高查找效率。

二分查找的基本思想是：

首先确定数组的中间位置mid。
将目标元素与mid位置的元素进行比较。
如果目标元素等于mid位置的元素，则查找成功。
如果目标元素小于mid位置的元素，则在左半部分继续进行二分查找。
如果目标元素大于mid位置的元素，则在右半部分继续进行二分查找。
重复以上步骤，直到找到目标元素或者确定目标元素不存在。

二分查找的时间复杂度为O(logn)，其中n为数组的长度。由于每次都将查找范围缩小一半，因此效率较高。

三、例子

假设我们有一组数据为{1,2,3,4,5,6,7}；

需要查找的元素为：6.

第一步：定义两个指针i和j，将i的值赋值为0，j的值赋值为数组的长度-1，中间元素m的下标为（0+6）/2 =3，这里请注意，下标为3对应的数字为4哦，不要搞混了。

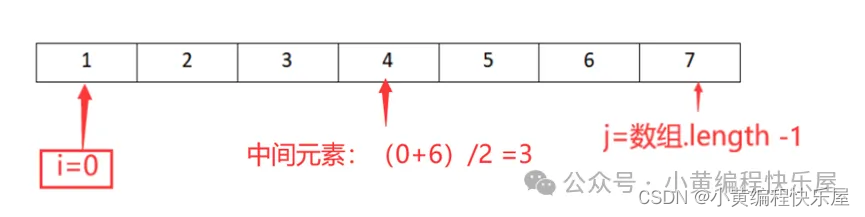
第二步：将中间的数比较我们想要查找的目标数字6，我们发现4<6,证明我们需要找的数在数字的右边部分，所以我们将i=m+1=3+1=4, j不变，所以m = ( i + j ) / 2=5。

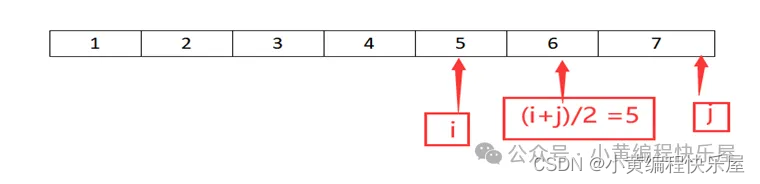
第三步：我们通过比较发现下标为5对应的数字6跟我们的目标数字相等，所以我们返回m。这样我们就查到了数据。

以下是另外一个示例过程，

假设我们有一个升序数组arr = {1, 3, 5, 7, 9}，并且我们按顺序查找数字1到2。

查找数字1：

l 初始时，i = 0，j = 4，计算m = (0 + 4) / 2 = 2。

l 因为arr[m] = 5大于目标值1，所以更新j = m - 1 = 1。

l 下一轮，m = (0 + 1) / 2 = 0。

l 因为arr[m] = 1等于目标值1，查找成功，返回索引m = 0。

查找数字2：

l 初始时，i = 0，j = 4，计算m = (0 + 4) / 2 = 2。

l 因为arr[m] = 5大于目标值2，所以更新j = m - 1 = 1。

l 下一轮，m = (0 + 1) / 2 = 0。

l 因为arr[m] = 1小于目标值2，所以更新i = m + 1 = 1。

l 但此时i已经大于j，说明目标值2不在数组中，查找失败，返回-1。

Java代码：（左闭合右闭合）

public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) { // 在左边
j = m - 1;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
注意：>>> 为无符号右移，就是将左操作数计算为无符号数，并将该数字的二进制表示形式移位为右操作数指定的位数，取模 32。向右移动的多余位将被丢弃，零位从左移入。其符号位变为 0，因此结果始终为非负数。与其他按位运算符不同，零填充右移返回一个无符号 32 位整数。

在这里使用无符号右移而不使用÷2操作是为了防止数据过大导致溢出。

例如：举个例子，现在假设我们有一个需要查找的数组a, a的长度比较大，为int的最大值也就是Integer.MAX_VALUE,我们假设我们要找的目标参数在右边，也就是i指针下一次指向Integer.MAX_VALUE/2。我们看看实际运行效果。我们可以看到，m的值竟然算出了负数，一个数组的下标很显然是不会等于负数的。所以我们需要使用>>>无符号右移符号。

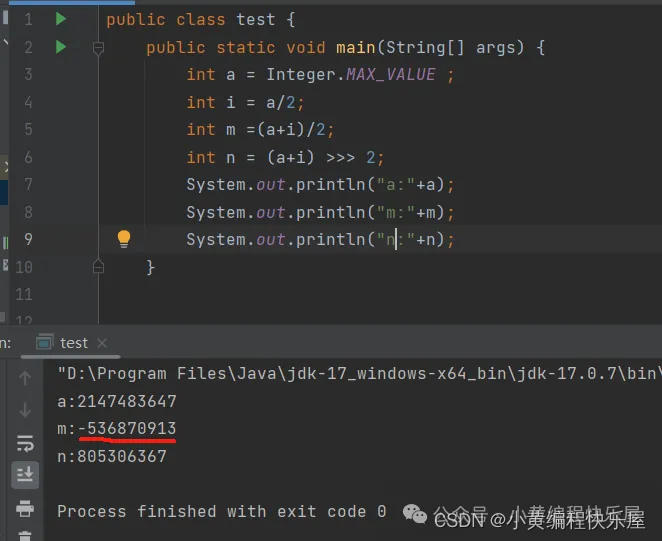
Java代码：

public class test {
public static void main(String[] args) {
int a = Integer.MAX_VALUE ;
int i = a/2;
int m =(a+i)/2;
int n = (a+i) >>> 2;
System.out.println(“a:”+a);
System.out.println(“m:”+m);
System.out.println(“m:”+n);
}

}
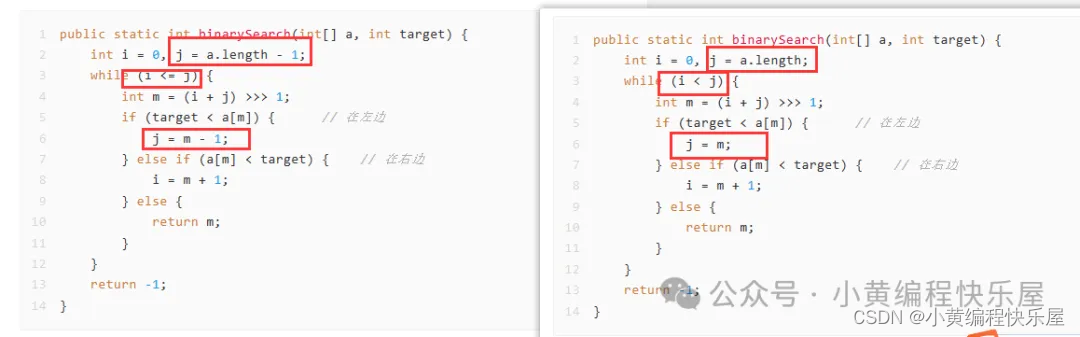
二分查找的另一种写法

Java代码：（左闭合右开[i, j)）

public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length;
while (i < j) {
int m = (i + j) >>> 1;
if (target < a[m]) { // 在左边
j = m;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
注意比较：j = a.length， while (i < j) ， j = m;这三个地方的不一样。