参考文章:突破传统RAG限制!Adaptive-RAG实现高效复杂查询处理
在人工智能领域,大型语言模型(LLMs)的发展日新月异,它们在多种任务中展现出了卓越的性能。然而,尽管LLMs在处理问题时表现出色,但它们仍然受限于模型内部知识的存储和更新。为了解决这一问题,研究者们提出了检索增强型大型语言模型(Retrieval-Augmented Large Language Models, LLMs),该模型通过结合外部知识库中的非参数知识,有效提升了问题回答的准确性。但是,现有的方法在处理不同复杂度的查询时存在效率和准确性的平衡问题。本文将深入探讨一篇关于自适应检索增强型LLMs的新方法——Adaptive-RAG,并分析其动机、方法、实验验证、创新点以及存在的不足。
传统的LLMs在处理问题时,依赖于其内部存储的知识,这导致了两个主要问题:一是知识可能过时,二是对于特定领域的复杂问题,模型可能缺乏足够的信息来给出准确的答案。为了克服这些限制,检索增强型LLMs应运而生,它们通过访问外部知识库来获取与输入相关的信息,并将这些信息整合到模型中,以提高回答的准确性和时效性。
然而,现有的检索增强型LLMs方法在处理不同复杂度的查询时,要么对于简单查询过于复杂,造成不必要的计算开销,要么对于复杂查询的处理不够充分。鉴于此,研究者们提出了Adaptive-RAG框架,旨在根据查询的复杂度动态选择最合适的策略,以实现在简单查询和复杂查询之间的平衡。
Adaptive-RAG框架的核心思想是根据查询的复杂度自适应地调整检索策略。具体来说,该框架包括以下几个关键步骤:
- 查询复杂度评估:首先,使用一个小型的语言模型(称为分类器)来预测输入查询的复杂度。这个分类器被训练为将查询分为三类:简单(A)、中等(B)和复杂(C)。
- 策略选择:根据查询的复杂度,框架动态选择从最简单的非检索方法到单步检索方法,再到多步检索方法的策略。
- 检索执行:对于需要检索的查询,框架将执行检索模块,从外部知识库中检索相关信息,并将这些信息传递给LLM。
- 答案生成:最后,LLM结合检索到的信息(如果有的话)生成最终的答案。
整个方法的思想如下:
- 查询复杂度分类器:分类器的设计是基于一个小型的预训练语言模型,通过自动收集的标签来训练。标签的获取有两种方式:一是基于模型预测结果的自动标注,二是基于数据集中固有的归纳偏差。
- 检索策略的实现:根据分类器的输出,框架将选择相应的检索策略。例如,对于标记为“A”的简单查询,直接使用LLM生成答案;对于标记为“B”的中等复杂度查询,执行单步检索;对于标记为“C”的复杂查询,则采用多步检索策略。
- 效率与准确性的平衡:Adaptive-RAG的目标是在保持高准确性的同时,尽可能减少计算资源的消耗。通过自适应选择最合适的检索策略,框架能够在处理简单查询时避免不必要的计算开销,而在处理复杂查询时提供充分的信息支持。
Adaptive-RAG(Adaptive Retrieval-Augmented Generation)是一种新型的问答框架,旨在通过动态选择最合适的检索策略来处理不同复杂度的查询。以下是该方法的详细描述:
1、查询复杂度评估
- 分类器设计:Adaptive-RAG使用一个小型的语言模型作为分类器,该分类器的任务是预测输入查询的复杂度级别。分类器有三个输出类别:简单(A)、中等(B)和复杂(C),分别对应不同的检索策略。
- 自动标注:分类器的训练数据是通过自动标注获得的。对于每个查询,框架会使用三种不同的检索增强型LLM策略(无检索、单步检索和多步检索)进行处理,并根据这些策略的预测结果来确定查询的复杂度标签。
- 数据集归纳偏差:除了基于模型预测的标注外,框架还利用数据集中的固有偏差来进行标注。例如,单步问答数据集中的查询通常适合使用单步检索策略,而多步问答数据集中的查询则更适合使用多步检索策略。
2、策略选择与执行
- 非检索方法:对于被分类器标记为简单的查询(A),Adaptive-RAG直接使用LLM生成答案,不进行外部知识检索。
- 单步检索方法:对于中等复杂度的查询(B),框架执行一次检索,获取相关信息,并将其与查询一起输入到LLM中,以生成答案。
- 多步检索方法:对于复杂的查询(C),Adaptive-RAG采用迭代的方式,多次访问检索器和LLM,通过Chain-of-Thought推理和文档检索相结合的方式,逐步构建答案。
3、效率与准确性的平衡
- 自适应调整:Adaptive-RAG的核心优势在于能够根据查询的实际复杂度自适应地调整检索策略,从而在保持高准确性的同时,减少不必要的计算开销。
- 无缝切换:由于LLM和检索器的操作对于不同的输入是一致的,Adaptive-RAG能够在不同复杂度的查询之间无缝切换,无需改变模型架构或参数。
为了验证Adaptive-RAG的有效性,研究者们在多个开放域问答数据集上进行了实验,这些数据集包括单跳和多跳查询,覆盖了从简单到复杂的多种查询类型。
实验设置
- 数据集:使用了包括SQuAD、Natural Questions、TriviaQA、MuSiQue、HotpotQA和2WikiMultiHopQA在内的多个数据集。
- 评估指标:采用了F1分数、精确匹配(EM)和准确率(Acc)作为有效性指标,以及检索和生成步骤的数量和平均查询响应时间作为效率指标。
- 模型配置:实验中使用了FLAN-T5系列模型(包括XL和XXL版本)和GPT-3.5模型作为基础LLM,并使用了BM25作为检索模型。
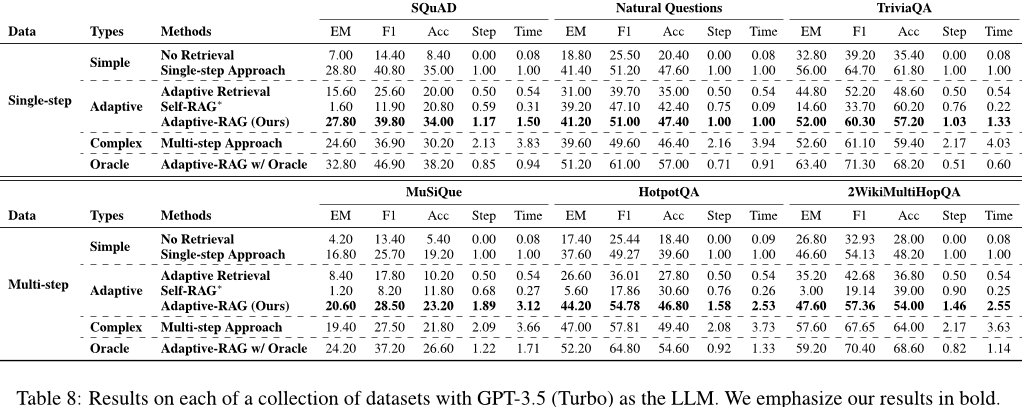
实验结果
- 性能提升:Adaptive-RAG在多个数据集上都取得了优于现有方法的性能,特别是在处理复杂查询时,其准确性和效率的提升更为显著。
- 效率分析:实验结果显示,Adaptive-RAG在处理简单查询时,能够有效减少检索步骤和响应时间;而在处理复杂查询时,虽然检索步骤增加,但通过精确的多步检索,提高了答案的准确性。
- 对比分析:与固定检索策略的方法相比,Adaptive-RAG展现出了更好的适应性和灵活性,能够根据查询的实际需求动态调整检索行为。
Adaptive-RAG通过自适应地选择检索策略,成功地解决了现有检索增强型LLMs在处理不同复杂度查询时面临的效率和准确性平衡问题。实验结果表明,该方法在多个开放域问答数据集上都取得了显著的性能提升。未来,通过进一步优化分类器和检索策略,Adaptive-RAG有望在更广泛的应用场景中发挥更大的作用。
论文详解
这篇论文介绍了一种名为Adaptive-RAG的新方法,用于提高问答系统的效率和准确性。传统的问答系统无法处理复杂的多步查询,而该方法可以根据查询复杂度动态选择最合适的策略,包括迭代式和单步式的检索增强语言模型以及无检索方法。为了实现这一目标,作者们设计了一个分类器,通过自动收集标签来预测查询的复杂程度,并利用数据集中的内在归纳偏见进行训练。实验结果表明,该方法在多个开放领域的问答数据集上表现出色,比其他相关基准方法更高效、准确。


方法描述
该论文提出了一个基于适应性检索增强的语言模型(Adaptive Retrieval-Augmented Generation),旨在根据查询复杂度选择最合适的策略来处理问题。具体来说,他们使用了三种不同的检索增强策略:非检索、单步和多步,然后设计了一个分类器来确定每个查询的复杂度,并相应地选择最适合的策略。这种方法可以提高问答系统的准确性和并发性,特别是在需要合成多个来源文档信息并推理它们的情况下。
方法改进
该方法的主要改进是通过动态调整查询处理策略来适应不同复杂度的查询。与传统的单一策略相比,这种自适应方法可以在简单和复杂的查询之间实现平衡,提高了系统的效率和准确性。
解决的问题
该方法解决了传统检索增强语言模型在处理不同复杂度查询时的局限性。它可以根据查询的复杂程度自动选择最适合的策略,从而提高系统的效果。此外,由于该方法不需要改变内部模型架构或参数,因此它可以无缝地适应不同类型和难度级别的查询。

论文实验
本文主要介绍了在问答系统中使用基于检索的预训练语言模型(Retrieval-Augmented Language Model,RAG)的研究,并提出了一种新的适应性策略——Adaptive-RAG。该方法可以根据查询复杂度自适应地选择是否进行文档检索和多次迭代生成答案,以提高效率和效果。本文进行了多项实验来验证Adaptive-RAG的有效性和效率,并与其他相关方法进行了比较。
首先,本文将单步和多步策略进行了比较,结果表明简单策略的效果不如复杂策略,但复杂策略的成本更高。因此,本文提出了Adaptive-RAG来解决这个问题。其次,本文还对不同类型的查询进行了比较,包括单-hop和多-hop查询,以及不同的模型和数据集。实验结果表明,Adaptive-RAG比其他方法具有更好的效果和更高的效率。
此外,本文还分析了Adaptive-RAG的一些细节问题,如分类器性能、训练数据、分类器大小等。最后,本文通过一个案例研究展示了Adaptive-RAG相对于Adaptive Retrieval的优势。
总之,本文提出的Adaptive-RAG是一种有效的适应性策略,可以显著提高问答系统的效率和效果。同时,本文也提供了一些有用的指导,帮助研究人员更好地设计和优化基于检索的语言模型。

文章优点
该论文提出了一种新的QA系统框架——Adaptive Retrieval-Augmented Generation(Adaptive-RAG),可以动态调整其处理策略以适应不同复杂度的查询。该框架使用一个较小的语言模型来预测输入查询的复杂度,并根据预测结果选择最适合的处理策略。这种方法能够平衡简单和复杂的查询,提高整体准确性和效率。作者通过实验验证了该框架的有效性和效率,并指出了一些潜在的改进方向。
方法创新点
该论文的主要贡献在于提出了Adaptive-RAG框架,该框架可以根据查询的复杂度自动选择最适合的处理策略。此外,该论文还提出了一种新颖的分类器,用于预测查询的复杂度。这种分类器不需要人工标注数据,而是利用已有的数据集中的信息自动生成训练数据。这些创新点使得该框架具有较高的可扩展性和实用性。
未来展望
尽管该论文提出的Adaptive-RAG框架已经取得了显著的进展,但仍然存在一些潜在的改进方向。例如,可以进一步优化分类器的设计,使其更加精确地预测查询的复杂度;还可以探索如何将Adaptive-RAG与其他技术相结合,以实现更高效、更准确的QA系统。总之,该论文为QA系统的未来发展提供了一个有前途的方向。